
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разделенные разности. Интерполяционный многочлен в форме НьютонаСодержание книги
Поиск на нашем сайте Для функции
разделенными разностями первого порядка называют отношения
На основе разделенных разностей первого порядка вычисляют разделенные разности второго порядка
Вообще, если определены конечные разности
Таким образом, для ( Для вычисления разделенных разностей удобно пользоваться табличной формой. Такая таблица разделенных разностей имеет следующий вид (для примера взят случай
Интерполяционный многочлен Лагранжа выражается через разделенные разности следующей формулой:
Эта форма записи интерполяционного многочлена и носит название интерполяционного многочлена Ньютона. П р и м е р 3. Применим формулу (4.7) к данным, приведенным в примерах 1 и 2. •
В таблице выделены значения функции и разделенных разностей, которые войдут в формулу (4.7):
Численное интегрирование Задача численного интегрирования. Если для функции
Но на практике, как правило, найти первообразную Хотя из определения интеграла Для получения формул численного интегрирования используют замену функции
где
где При численном интегрировании обычно рассматривают разбиения отрезка интегрирования Пусть отрезок
т. е.
Подынтегральную функцию можно также заменить ее значением в середине каждого отдельного интервала сетки В зависимости от выбора значения интерполяционного многочлена Лагранжа нулевой степени на каждом шаге сетки получаются следующие формулы прямоугольников:
Для аналитически заданных подынтегральных функций
где
Предельная погрешность этой формулы
где Формула Симпсона (параболических трапеций). Подынтегральная кривая
При одном и том же количестве интервалов деления отрезка интегрирования
где П р и м е р 1. Применим формулу Симпсона к вычислению интеграла
• Четвертая производная для подынтегральной функции
Возьмем Таблица значений
Используя табличные данные, получаем:
Погрешность при округлении вычисленных значений функции не превосходит величины
(при вычислении каждого значения
Формулы численного интегрирования Гаусса и Чебышева. Квадратурные формулы численного интегрирования Гаусса и Чебышева применяют в тех случаях, когда требуется большая точность значения интеграла, но получение значений подынтегральной функции при большом числе значений аргумента по каким-либо причинам оказывается затруднительным. Интеграл
приводится сначала к виду Квадратурная формула Гаусса:
Абсциссы
Предельная погрешность квадратурной формулы Гаусса равна
Квадратурные формулы Чебышева применяются тоже после предварительной замены переменной (6.11); они имеют вид
Абсциссы
Применение равных весов будет минимизировать случайную погрешность в тех случаях, когда значения П р и м е р 2. Вычислить по формуле Гаусса приближенное значение интеграла
взяв • Заменой
Используя табличные значения абсцисс
Рассмотренный здесь интеграл вычисляется точно, и его значение равно
3. Численное дифференцирование Постановка задачи При решении практических задач часто требуется найти производные указанных порядков от функции Для этого на отрезке Если для интерполирующей функции известна погрешность
то погрешность производной
т.е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же справедливо для производных высших порядков. Приближенное дифференцирование является менее точной операцией, чем интерполирование. Близость друг к другу ординат двух кривых
Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона Пусть на отрезке Заменим функцию
где Произведя перемножение биномов и приведя подобные, получим:
Так как
то
Аналогично, так как
то
Таким образом можно вычислить производную любого порядка. При нахождении производных Формулы (6.3) и (6.4) упрощаются, если нужно подсчитать производные в узлах интерполяции. Полагая
Пусть
Полагая
Так как
Аналогично находится
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 и узлов интерполяции
и узлов интерполяции
 (4.4)
(4.4) (4.5)
(4.5) - го порядка
- го порядка  , то разделенные разности (
, то разделенные разности ( ) - го порядка находят при помощи формулы
) - го порядка находят при помощи формулы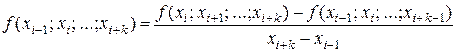 . (4.6)
. (4.6) ) узлов интерполяции могу быть построены разделенные разности до
) узлов интерполяции могу быть построены разделенные разности до  - го порядка включительно; разделенные разности более высоких порядков равны нулю.
- го порядка включительно; разделенные разности более высоких порядков равны нулю. ):
):
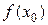




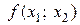






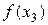
 (4.7)
(4.7)
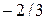





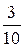

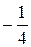


 , можно найти первообразную
, можно найти первообразную  , то определенный интеграл
, то определенный интеграл  можно вычислить по формуле
можно вычислить по формуле =
= 
 его можно найти с любой точностью, но этот прием замены определенного интеграла интегральной суммой практически мало пригоден из-за медленной сходимости
его можно найти с любой точностью, но этот прием замены определенного интеграла интегральной суммой практически мало пригоден из-за медленной сходимости  к
к 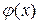 . Чаще всего подынтегральную функцию заменяют интерполирующим многочленом Лагранжа различной степени
. Чаще всего подынтегральную функцию заменяют интерполирующим многочленом Лагранжа различной степени 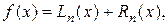 (6.1)
(6.1) – остаточный член интерполяции. Тогда
– остаточный член интерполяции. Тогда (6.2)
(6.2) – остаточный член формулы численного интегрирования (погрешность этой формулы).
– остаточный член формулы численного интегрирования (погрешность этой формулы). (равномерная сетка),
(равномерная сетка), – шаг сетки. Обозначим через
– шаг сетки. Обозначим через  соответствующие значения функции
соответствующие значения функции  .
. Формулы прямоугольников. Подынтегральная функция
Формулы прямоугольников. Подынтегральная функция  -ом шаге сетки интерполяционным многочленом Лагранжа нулевой степени
-ом шаге сетки интерполяционным многочленом Лагранжа нулевой степени  ,
,  , (
, ( при перемещении по сетке справа налево). В случае
при перемещении по сетке справа налево). В случае  это означает, что площадь каждой полоски, на которые разбивается криволинейная трапеция, заменяется площадью прямоугольника высотой
это означает, что площадь каждой полоски, на которые разбивается криволинейная трапеция, заменяется площадью прямоугольника высотой 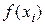 и основанием
и основанием  (рис. 7).
(рис. 7). (
( ), но в том случае, если она задана таблицей, это значение приходится находить, как правило, интерполированием, что вносит дополнительную погрешность (трудно поддающуюся оценке).
), но в том случае, если она задана таблицей, это значение приходится находить, как правило, интерполированием, что вносит дополнительную погрешность (трудно поддающуюся оценке). , (6.3)
, (6.3) , (6.4)
, (6.4) . (6.5)
. (6.5)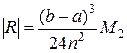 , (6.6)
, (6.6) – наибольшее значение
– наибольшее значение  на отрезке
на отрезке 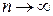 .
. Формула трапеций. Подынтегральная функция
Формула трапеций. Подынтегральная функция  ,
,  (6.7)
(6.7) (6.8)
(6.8)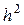 относительно шага сетки
относительно шага сетки  .
. (формула (4.3)),
(формула (4.3)),  . На равномерной сетке и четном количестве интервалов
. На равномерной сетке и четном количестве интервалов  деления отрезка интегрирования
деления отрезка интегрирования 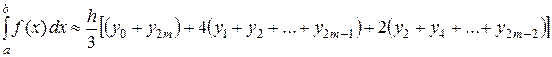 . (6.9)
. (6.9) , (6.10)
, (6.10) – наибольшее значение
– наибольшее значение  на отрезке
на отрезке  .
. . Ее абсолютное значение на отрезке интегрирования
. Ее абсолютное значение на отрезке интегрирования 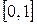 не превосходит 12. Поэтому для погрешности получаем
не превосходит 12. Поэтому для погрешности получаем .
.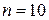
 . Это гарантирует погрешность, не превосходящую 0,000007. Вычисляем значения подынтегральной функции
. Это гарантирует погрешность, не превосходящую 0,000007. Вычисляем значения подынтегральной функции  с точностью до 0.000005 и оформляем их в табличном виде.
с точностью до 0.000005 и оформляем их в табличном виде.



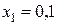


















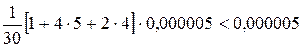
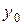 ,
,  , … совершается ошибка до 0,000005, которая при сложении и вычитании может возрасти в соответствующее число раз; при делении возможная погрешность соответственно уменьшается). Следовательно, общая погрешность — формулы (6.9) и от округления значений функции — не превосходит величины 0,000012, так что
, … совершается ошибка до 0,000005, которая при сложении и вычитании может возрасти в соответствующее число раз; при делении возможная погрешность соответственно уменьшается). Следовательно, общая погрешность — формулы (6.9) и от округления значений функции — не превосходит величины 0,000012, так что •
• ,
, 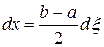 , (6.11)
, (6.11) .
. . (6.12)
. (6.12) и веса
и веса  для некоторых значений
для некоторых значений 












 .
. . (6.12)
. (6.12)
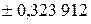










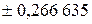



 ,
, .
. преобразуем интеграл к промежутку
преобразуем интеграл к промежутку  . Получим:
. Получим: ,
,  .
. :
: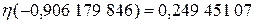 ,
,  ,
,  ,
, ,
,  . Взяв из той же таблицы соответствующие веса
. Взяв из той же таблицы соответствующие веса 
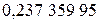 +
+ 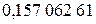 )+
)+  +
+  )=
)=  .
. Сравнивая, делаем вывод, что в вычисленном приближенном значении интеграла все знаки верны, т. е. формула Гаусса дает большую точность результата. Вместе с тем обращает на себя внимание то, что абсциссы
Сравнивая, делаем вывод, что в вычисленном приближенном значении интеграла все знаки верны, т. е. формула Гаусса дает большую точность результата. Вместе с тем обращает на себя внимание то, что абсциссы  , заданной таблично, или, в силу сложности аналитического выражения функции
, заданной таблично, или, в силу сложности аналитического выражения функции  функцию
функцию  (чаще всего интерполирующим полиномом
(чаще всего интерполирующим полиномом  ), затем полагают
), затем полагают  при
при  . Аналогично поступают при нахождении производных высших порядков от функции
. Аналогично поступают при нахождении производных высших порядков от функции  ,
, ,
, на отрезке
на отрезке  и
и  , то есть малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.
, то есть малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента. :
:  ,
,  , и известны значения функции в этих точках
, и известны значения функции в этих точках  . Требуется найти производные
. Требуется найти производные  на отрезке
на отрезке  , воспользовавшись первой интерполяционной формулой Ньютона:
, воспользовавшись первой интерполяционной формулой Ньютона: (6.1)
(6.1) .
. (6.2)
(6.2) ,
, (6.3)
(6.3) ,
, . (6.4)
. (6.4)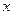 в качестве
в качестве  следует брать ближайшее к
следует брать ближайшее к  ,
,  , получаем:
, получаем: , (6.5)
, (6.5) . (6.6)
. (6.6) и
и  , тогда
, тогда  . Но
. Но  . Тогда, если
. Тогда, если  , то
, то (6.7)
(6.7) - ограниченной и учитывая, что
- ограниченной и учитывая, что  , получаем при
, получаем при  . (6.8)
. (6.8)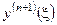 сложно определить, то при малом шаге
сложно определить, то при малом шаге  принято считать
принято считать  . Тогда (6.8) примет вид:
. Тогда (6.8) примет вид: . (6.9)
. (6.9)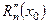 и так далее.
и так далее.


