Т. е и при делении приближенных величин их относительные погрешности складываются.
Похожие статьи вашей тематики
·  , ,
 . .
Погрешность степени
Предельная относительная погрешность  – той степени числа – той степени числа  в в  раз больше предельной относительной погрешности самого этого числа. раз больше предельной относительной погрешности самого этого числа.
Погрешность корня
Предельная относительная погрешность корня  – й степени числа – й степени числа  в в  раз меньше предельной относительной погрешности самого числа раз меньше предельной относительной погрешности самого числа  . .
П р и м е р 2. Пусть  , ,  . Вычислить . Вычислить  , ,  , ,  , ,  . Оценить абсолютные и относительные погрешности результатов. . Оценить абсолютные и относительные погрешности результатов.
• Имеем  , ,  , ,  , , 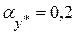 . Тогда . Тогда  , откуда , откуда  и и  . Относительные погрешности суммы и разности будут равны: . Относительные погрешности суммы и разности будут равны:
 , ,
 . .
Для абсолютных погрешностей произведения и частного будем иметь:
 , ,
 . .
Относительные погрешности полученных результатов для  и и  будут: будут:
 , ,
 . • . •
Вычисления без строгого учета погрешностей проводят на основе записи приближенных чисел с использованием описанного выше понятия верных (точных) цифр числа. При этом надо иметь ввиду, что отбрасывание сомнительных цифр, сопровождаемое округлениями, всегда увеличивает область неопределенности приближенного числа. Поэтому, если приближенные числа не носят окончательного характера и с ними предполагается производить еще какие-то вычисления, то рекомендуется сохранять одну или две сомнительные цифры. При проведении вычислений без строгого учета погрешностей следует придерживаться следующих правил.
· При сложении и вычитании приближенных чисел в более точных числах берут на один десятичный знак больше, чем в наименее точном числе, а в результате запасной знак отбрасывают, соблюдая во всех случаях правило округления чисел. Из нескольких приближенных чисел наименее точным считается то, которое имеет наименьшее количество верных десятичных знаков;
· Чтобы сложить (вычесть) несколько приближенных чисел с заданной точность результата, эти числа округляют с одной запасной цифрой сверх заданной точности, складывают (вычитают) и в результате отбрасывают запасной знак. Если слагаемых более десяти (но менее ста) рекомендуется брать две запасные цифры, т. к. погрешности накапливаются;
· При умножении и делении более точное число округляют так, чтобы оно содержало на один верный знак больше, чем менее точное. В результате сохраняют столько значащих цифр, сколько их содержит наименее точное число.
· При возведении в квадрат и куб в результате сохраняют столько значащих цифр, сколько их имеет основание степени;
· При извлечении квадратного и кубического корня в результате сохраняют столько значащих цифр, сколько их имеет подкоренное число.
П р и м е р 3:
a) 18,384+12,65+36,84278+37,195682=18,384+12,65+36,843+37,196=107,073= 107,07.
b) 879,6–124,318739=879,6–124,32=755,28= 755,3.
c) Найти 83,6724379–15,3281375 с точностью до 0,01: 83,672–15,328=68,344= 68,34.
d)  . .
e)  . .
|