Формулы логики булевых функций
Определение 4.2. Формула логики булевых функций определяется индуктивно следующим образом:
1. Любая переменная, а также константы 0 и 1 есть формула.
2. Если A и B – формулы, то Ø A, A V B, A & B, A É B, A ~ B есть формулы.
3. Ничто, кроме указанного в пунктах 1–2, не есть формула.
Пример 4.1.
Выражение (Ø x V y)&((y É z) ~ x) является формулой.
Выражение Ø x & y É z Ø ~ x не является формулой.
Часть формулы, которая сама является формулой, называется подформулой.
Пример 4.2.
x &(y É z) – формула; y É z – ее подформула.
Определение 4.3. Функция f есть суперпозиция функций f 1, f 2,..., fn если f получается с помощью подстановок этих формул друг в друга и переименованием переменных.
Пример 4.3.
f 1 = x 1& x 2 (конъюнкция); f 2 = Ø x (отрицание).
Возможны две суперпозиции:
1) f = f 1(f 2) = (Ø x 1)&(Ø x 2) – конъюнкция отрицаний;
2) f = f 2(f 1) = Ø(x 1& x 2) – отрицание конъюнкции.
Порядок подстановки задается формулой.
Всякая формула задает способ вычисления функции, если известны значения переменных.
Пример 4.4.
Построим таблицу значений функции f (x 1, x 2, x 3) = Ø(x 2 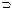 Ø x 3) ~ (Ø x 1V x 2). Ø x 3) ~ (Ø x 1V x 2).
Таблица 4.4 представляет последовательное вычисление этой функции.
Таблица 4.4
| x 1 x 2 x 3
| Ø x 3
| x 2 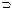 Ø x 3 Ø x 3
| Ø(x 2 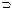 Ø x 3) Ø x 3)
| Ø x 1
| Ø x 1V x 2
| f (x 1, x 2, x 3)
| | 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
|
|
|
|
|
|
|
Таким образом, формула каждому набору аргументов ставит в соответствие значение функции. Следовательно, формула так же, как и таблица, может служить способом задания функции. В дальнейшем формулу будем отождествлять с функцией, которую она реализует. Последовательность вычислений функции задается скобками. Принято соглашение об опускании скобок в соответствии со следующей приоритетностью операций: Ø, &, V, É и ~.
Равносильные преобразования формул
В отличие от табличного задания представление функции формулой не единственно. Например, две различные формулы
Ø x 1VØ x 2 и Ø(x 1& x 2)
реализуют одну функцию – штрих Шеффера.
Две формулы, реализующие одну и ту же функцию, называются равносильными.
Равносильность формул A и B будем обозначать следующтм образом: A º B.
Для того, чтобы установить равносильность формул, можно составить таблицы значений функции для каждой формулы и сравнить их. Для равносильных формул эти таблицы совпадают. Другой способ установления равносильности формул заключается в использовании некоторых установленных равносильностей булевых формул.
|