
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3 Обратная матрица и ранг матрицыСодержание книги
Поиск на нашем сайте Лекция 3.1 «Обратная матрица и ранг матрицы» Учебные вопросы: 1. Ранг матрицы 2. Обратная матрица
Ранг матрицы Ранг данной матрицы Ранг матрицы равен наибольшему числу ее линейно независимых строк (или столбцов). Для квадратной матрицы Ранг суммы двух матриц
Пример. Найти ранг матрицы ◄ Ранг этой квадратной матрицы порядка
Пример. Найти ранг матрицы ◄ Ранг этой матрицы В общем случае для вычисления ранга матрицы ее сначала приводят к более простому виду с помощью так называемых элементарных преобразований, к которым относятся: 1) перестановка строк матрицы; 2) умножение какой-либо строки на одно и то же отличное от нуля число; 3) прибавление к элементам строки соответствующих элементов другой строки, предварительно умноженных на некоторое число. Можно показать, что элементарные преобразования не меняют ранга матрицы. Если с помощью элементарных преобразований получить нули ниже главной диагонали матрицы, то ранг исходной матрицы будет равен числу ненулевых строк преобразованной матрицы. Пример. С помощью элементарных преобразований вычислить ранг матрицы
◄ Умножим первую строку матрицы на –2 и прибавим ко второй строке:
Теперь умножим первую строку на –3 и сложим ее с третьей строкой, а затем вычтем из последней строки первую. Имеем ~ Умножая вторую строку получившейся матрицы на –2 и складывая ее с третьей строкой, а затем, складывая вторую строку с последней, получим матрицу ~ Преобразованная матрица имеет две ненулевые строки, следовательно, ранг матрицы А равен двум:
Обратная матрица Квадратная матрица
В противном случае матрица Квадратная матрица
где Квадратная матрица не вырождена в том и только том случае, если ее строки (столбцы) линейно независимы. Строки (столбцы) матрицы линейно независимы, если ни одна строка (столбец) не могут быть выражены в виде линейной комбинации остальных строк (столбцов). В противном случае строки (столбцы) линейно зависимы. Если матрицы
Пример. Дана матрица ◄ Находим определитель матрицы
Следовательно, по формуле (1.1.1)
Проводим проверку полученного результата:
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 есть такое число
есть такое число  , что по крайней мере один определитель
, что по крайней мере один определитель  - го порядка, получаемый из этой матрицы при удалении некоторых строк и/или столбцов, отличен от нуля, а все определители
- го порядка, получаемый из этой матрицы при удалении некоторых строк и/или столбцов, отличен от нуля, а все определители 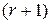 - го порядка равны нулю.
- го порядка равны нулю. ее ранг
ее ранг  . Эта матрица является невырожденной в том и только в том случае, если ее ранг
. Эта матрица является невырожденной в том и только в том случае, если ее ранг 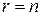 , т. е.
, т. е.  . Если же
. Если же  , то матрица является вырожденной.
, то матрица является вырожденной.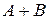 не больше суммы их рангов:
не больше суммы их рангов: .
. .
. удовлетворяет соотношению
удовлетворяет соотношению  . Единственный определитель 3-го порядка, получаемый из этой матрицы
. Единственный определитель 3-го порядка, получаемый из этой матрицы  . Ранг данной матрицы
. Ранг данной матрицы 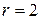 , т. к. по крайней мере один определитель 2-го порядка, получаемый из этой матрицы при удалении 3-й строки и 3-го столбца,
, т. к. по крайней мере один определитель 2-го порядка, получаемый из этой матрицы при удалении 3-й строки и 3-го столбца,  . ►
. ► .
. , т. к. из данной матрицы можно получить определители порядка не выше 2-го. Легко убедиться, что все три определителя 2-го порядка, которые можно получить из этой матрицы удалением поочередно его столбцов, равны нулю. Отсюда следует, что ранг данной матрицы
, т. к. из данной матрицы можно получить определители порядка не выше 2-го. Легко убедиться, что все три определителя 2-го порядка, которые можно получить из этой матрицы удалением поочередно его столбцов, равны нулю. Отсюда следует, что ранг данной матрицы  (каждый элемент матриц представляет собой определитель 1-го порядка). Уменьшение ранга этой матрицы по отношению к максимально возможному
(каждый элемент матриц представляет собой определитель 1-го порядка). Уменьшение ранга этой матрицы по отношению к максимально возможному 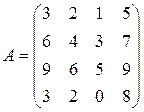 .
. ~
~  ~.
~. ~.
~. .
. . ►
. ►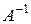 , определяемую условиями
, определяемую условиями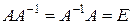 .
.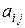 ) порядка
) порядка 
 ; в этом случае обратная матрица
; в этом случае обратная матрица  , (1.1.1)
, (1.1.1)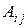 – алгебраические дополнения элементов
– алгебраические дополнения элементов  .
. не вырождены и число
не вырождены и число 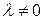 , то
, то ,
,  ,
,  .
. . Найти обратную матрицу
. Найти обратную матрицу  . Т. к.
. Т. к.  , делаем вывод, что матрица не вырождена и, следовательно, имеет обратную матрицу. Находим алгебраические дополнения для элементов матрицы:
, делаем вывод, что матрица не вырождена и, следовательно, имеет обратную матрицу. Находим алгебраические дополнения для элементов матрицы: ,
,  ,
,  ,
, ,
,  ,
,  ,
, ,
,  ,
,  .
. .
. . Делаем вывод, что результат правильный. ►
. Делаем вывод, что результат правильный. ►


