Знакопеременные ряды. Абсолютная и условная сходимость
Похожие статьи вашей тематики
Если не все члены ряда имеют одинаковые знаки, то ряд называется знакопеременным. В случае конечного числа членов, имеющих один знак, при исследовании сходимости эти члены можно отбросить и рассматривать остающийся знакопостоянный ряд. Исследование же рядов с бесконечным количеством положительных и отрицательных членов имеет некоторые принципиальные отличия от исследования знакопостоянных рядов.
Одним из важных достаточных признаков сходимости знакопеременного ряда является следующая теорема:
Ряд с членами произвольных знаков
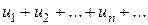 = = 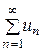 (3.6) (3.6)
сходится, если сходится ряд
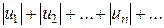 = = 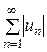 , (3.7) , (3.7)
составленный из абсолютных величин членов ряда (3.6).
В этом случае ряд (3.6) называется абсолютно сходящимся. Исследование сходимости абсолютно сходящегося знакопеременного ряда сводится к исследованию сходимости соответствующего ряда с положительными членами.
Пример. Исследовать сходимость ряда  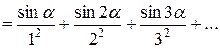 ., где ., где  – любое число. – любое число.
◄ Рассмотрим ряд, составленный из абсолютных величин исходного ряда: 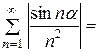 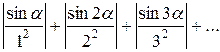 . Так как члены полученного положительного ряда не больше соответственных членов сходящегося ряда Дирихле . Так как члены полученного положительного ряда не больше соответственных членов сходящегося ряда Дирихле 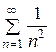 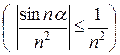 , исходный тоже сходится (абсолютно). ► , исходный тоже сходится (абсолютно). ►
Возможны случаи, когда ряд (3.6) сходится, а ряд (3.7) расходится. Тогда ряд называют неабсолютно, или условно сходящимся.
Таким образом, из расходимости ряда 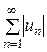 расходимость знакопеременного ряда расходимость знакопеременного ряда 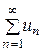 , вообще говоря, не следует. Однако, если, применяя к ряду , вообще говоря, не следует. Однако, если, применяя к ряду 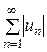 признак Даламбера (или признак Коши), получаем предел признак Даламбера (или признак Коши), получаем предел 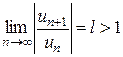 (или (или  ), то в этом случае оба ряда – ), то в этом случае оба ряда – 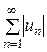 и и 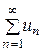 – расходятся. – расходятся.
Пример. Исследовать на сходимость ряд 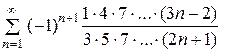 . .
◄ Рассмотрим ряд 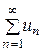 из абсолютных величин членов данного ряда: из абсолютных величин членов данного ряда: 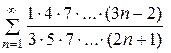 . Для исследования сходимости последнего ряда с положительными членами применим признак Даламбера: . Для исследования сходимости последнего ряда с положительными членами применим признак Даламбера:
 . .
Отсюда
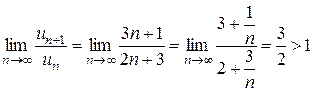 , ,
т. е. ряд с положительными членами расходится и, следовательно, исходный ряд не является абсолютно сходящимся. Кроме того, из 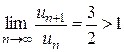 следует, что следует, что 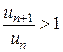 для всех номеров, начиная с некоторого и, следовательно, для всех номеров, начиная с некоторого и, следовательно, 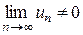 . Так как необходимое условие сходимости не выполняется, исходный ряд . Так как необходимое условие сходимости не выполняется, исходный ряд 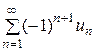 расходится. ► расходится. ►
Если ряд 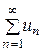 абсолютно сходится, то ряд, полученный из него любой перестановкой членов, также сходится и имеет ту же сумму, что и исходный (переместительное свойство абсолютно сходящихся рядов). абсолютно сходится, то ряд, полученный из него любой перестановкой членов, также сходится и имеет ту же сумму, что и исходный (переместительное свойство абсолютно сходящихся рядов).
Неабсолютно (условно) сходящиеся ряды переместительным свойством не обладают. Более того, можно так переставить члены неабсолютно сходящегося ряда, чтобы преобразованный ряд имел сумму, равную любому наперед заданному числу, или стал расходящимся (теорема Римана).
Пример. Рассмотрим ряд
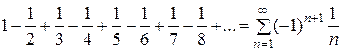 . .
Позже будет показано, что этот ряд является условно сходящимся. Обозначим его сумму через  (показано, что (показано, что 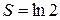 ). Умножим этот ряд на множитель ). Умножим этот ряд на множитель 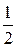 и запишем полученный ряд под исходным следующим образом: и запишем полученный ряд под исходным следующим образом:
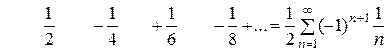
Так как последний ряд получен умножением сходящегося ряда на постоянное число, то он также будет сходящимся и его сумма будет равна 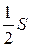 . Сложив теперь оба ряда почленно, соединяя вместе члены, стоящие друг под другом, получим . Сложив теперь оба ряда почленно, соединяя вместе члены, стоящие друг под другом, получим
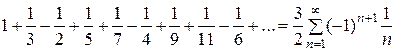 . .
Полученный при сложении двух сходящихся рядов будет также сходящимся, а его сумма равна 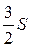 . Но этот ряд можно, очевидно, получить из исходного путем перестановки его членов. Таким образом, от перестановки сумма ряда умножилась на . Но этот ряд можно, очевидно, получить из исходного путем перестановки его членов. Таким образом, от перестановки сумма ряда умножилась на  . .
Знакопеременный ряд можно представить состоящим из двух рядов: ряда, составленного только из его положительных членов, и ряда, составленного только из его отрицательных членов. В случае абсолютно сходящегося ряда оба этих знакопостоянных ряда сходятся и его сумма равна разности сумм двух рядов с положительными членами. Для условно сходящегося ряда оба ряда расходящиеся, т. е. его нельзя рассматривать как разность двух сходящихся рядов, один из которых состоит из положительных членов данного ряда, а другой – из абсолютных величин его отрицательных членов.
|