Метод Фурье решения уравнений с частными производными
Похожие статьи вашей тематики
Метод Фурье (или метод разделения переменных), широко используемый при решении ряда задач математической физики, состоит в следующем. Искомая функция (решение), зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной переменной. После подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, решения которых вместе с краевыми условиями исходной задачи позволяют найти искомое решение.
Сущность этого метода рассмотрим на следующем примере.
Пусть требуется найти решение одномерного волнового уравнения
 , (5.31) , (5.31)
удовлетворяющее граничным условиям
 , ,  (5.32) (5.32)
(для струны эти условия означают, что ее концы при  и и  неподвижны (закреплены)), и начальным условиям неподвижны (закреплены)), и начальным условиям
 , ,  . (5.33) . (5.33)
Ищем решение в виде произведения
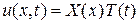 , ,
подставив которое в исходное уравнение, имеем  и, разделив это равенство на и, разделив это равенство на  , получаем , получаем
 . .
Каждое отношение зависит здесь от своей переменной, а потому равенство возможно только в том случае, когда каждое из этих отношений равно постоянному числу. Полагая  , ,  , где постоянная , где постоянная  (случай (случай  будет рассмотрен позднее), получаем два уравнения: будет рассмотрен позднее), получаем два уравнения:
 , (5.34) , (5.34)
 . (5.35) . (5.35)
Оба уравнения являются линейными однородными уравнениями 2-го порядка с постоянными коэффициентами, характеристические уравнения которых при  имеют комплексные корни. Общие решения этих уравнений будут: имеют комплексные корни. Общие решения этих уравнений будут:
 , (5.36) , (5.36)
 , (5.37) , (5.37)
где  , ,  , ,  , ,  – произвольные постоянные. – произвольные постоянные.
Постоянные  и и  определяются из граничных условий (5.32). Так как определяются из граничных условий (5.32). Так как  не равна тождественно нулю (в противном случае не равна тождественно нулю (в противном случае  ), функция ), функция  должна удовлетворять условиям (5.32), т. е. должно быть должна удовлетворять условиям (5.32), т. е. должно быть  , , 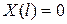 . Отсюда получаем систему уравнений: . Отсюда получаем систему уравнений:

Из первого уравнения находим  . Тогда из второго уравнения следует . Тогда из второго уравнения следует
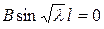 . .
Так как  (в противном случае было бы (в противном случае было бы  и и  ), имеем тригонометрическое уравнение ), имеем тригонометрическое уравнение  , из которого получаем , из которого получаем
 ( ( =1, 2, …) (5.38) =1, 2, …) (5.38)
( =0 не берется, так как и в этом случае было бы =0 не берется, так как и в этом случае было бы  и и  ). Числа ). Числа  называются собственными числами для уравнения (5.34) с граничными условиями (5.32), а соответствующие им решения называются собственными числами для уравнения (5.34) с граничными условиями (5.32), а соответствующие им решения
 (5.39) (5.39)
– собственными функциями.
Если же взять  , то уравнение (5.34) будет иметь отличное от нуля общее решение , то уравнение (5.34) будет иметь отличное от нуля общее решение
 , ,
которое не может удовлетворять граничным условиям (5.32).
Для каждого собственного числа  получается решение исходного волнового уравнения (5.31): получается решение исходного волнового уравнения (5.31):
 , (5.40) , (5.40)
которое удовлетворяет граничным условиям (5.32) (постоянная  включена в включена в  и и  ). Так как заданное волновое уравнение линейное и однородное, то сумма решений ). Так как заданное волновое уравнение линейное и однородное, то сумма решений
 (5.41) (5.41)
также будет его решением, удовлетворяющим граничным условиям (5.32). Это решение должно еще удовлетворять начальным условиям (5.33). Подставив  в (5.41), получаем из первого начального условия в (5.41), получаем из первого начального условия
 . (5.42) . (5.42)
Дифференцируя члены равенства (5.41) по  и подставляя затем и подставляя затем  , получаем из второго начального условия , получаем из второго начального условия
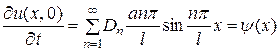 . (5.43) . (5.43)
Из этих равенств следует, что если числа  являются коэффициентами ряда Фурье функции являются коэффициентами ряда Фурье функции 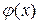 , т. е. если , т. е. если
 , ,
а числа  – коэффициентами Фурье функции – коэффициентами Фурье функции  , т. е. если , т. е. если
 , ,
то ряд (5.41) представляет функцию  , которая является искомым решением задачи (5.31) – (5.33). , которая является искомым решением задачи (5.31) – (5.33).
В случае, когда исходное уравнение в частных производных является неоднородным, т. е. в характеризуемом этим уравнением физическом процессе имеются внешние силы и источники, предварительно находится система собственных функций соответствующего однородного уравнения, и решение ищется в виде ряда по этим собственным функциям с переменными коэффициентами.
|