
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы дифференциальных уравненийСодержание книги
Поиск на нашем сайте
Система уравнений вида
называется нормальной системой дифференциальных уравнений. Число уравнений, входящих в систему, называется порядком этой системы. Возьмем в качестве независимой переменной
где введены обозначения Решением системы (9.28) на некотором промежутке называется совокупность функций Общим решением системы (9.28) является совокупность функций
которая при любых значениях постоянных Решение, которое получается из общего решения при фиксированных значениях произвольных постоянных, называется частным решением системы. Задача Коши для системы дифференциальных уравнений (9.28) состоит в нахождении частного решения этой системы Система (9.28) имеет физический смысл и называется динамической системой. Она определяет скорость Одним из основных методов решения систем дифференциальных уравнений является метод исключения неизвестных, с помощью которого система дифференциальных уравнений (9.28) сводится к дифференциальному уравнению второго порядка от одной неизвестной функции. Рассмотрим этот метод на примере. Пример 9.16. Найти решение системы ДУ
Решение. Решение системы будем проводить в несколько этапов. 1) Выразим из первого уравнения системы
2) Подставим (9.30) во второе уравнение системы и преобразуем его:
Получили линейное однородное дифференциальное уравнение второго порядка относительно неизвестной функции 3) Решая уравнение (9.31), находим функцию
– общее решение уравнения (9.31). 4) Подставив (9.32) в формулу (9.30), находим функцию
Таким образом, получим общее решение системы (9.29):
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Решить дифференциальные уравнения 1. 2. 3. 4. 5. 6. 7. 8. Найти общее решение ДУ второго порядка
9. 10. 11. 12. 13. 14. 15. 16. Найти общее решение системы дифференциальных уравнений
КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №9
Модуль 10. Ряды Числовые ряды. Основные понятия Определение. Пусть
называется числовым рядом, числа Например, числовыми рядами являются следующие выражения:
Определение. Сумма конечного числа
называется Таким образом,
Определение. Если существует конечный предел последова-тельности
то ряд называется сходящимся, а число
Если предел последовательности Выражение вида
представляющее собой числовой ряд, называется Для сходящегося ряда можно записать равенство
Поскольку для сходящегося числового ряда
Например, рассмотрим ряд
представляющий собой сумму членов бесконечно убывающей геометрической прогрессии со знаменателем
Следовательно, ряд сходится и его сумма Ряд
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.219.64 (0.01 с.) |


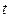 . Пусть
. Пусть  – функции этой переменной. Рассмотрим систему дифференциальных уравнений 2-го порядка
– функции этой переменной. Рассмотрим систему дифференциальных уравнений 2-го порядка (9.28)
(9.28)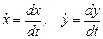 .
. , которая обращает все уравнения системы на этом промежутке в тождества.
, которая обращает все уравнения системы на этом промежутке в тождества.
 является решением системы.
является решением системы.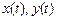 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 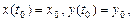 где
где 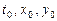 – заданные числа.
– заданные числа. движущейся в плоскости материальной точки в любой момент времени
движущейся в плоскости материальной точки в любой момент времени 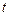 . Решение системы (9.28)
. Решение системы (9.28) 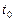 .
.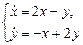 (9.29)
(9.29)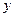 :
: . (9.30)
. (9.30)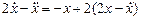 ,
, 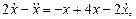
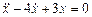 (9.31)
(9.31)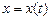 .
. :
: 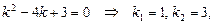
 (9.32)
(9.32)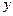 :
:
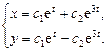
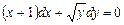 .
.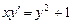 .
. .
.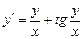 .
.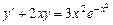 ,
, 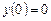 .
.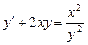 .
. .
. ,
, 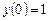 ,
,  .
. .
.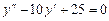 .
.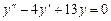 .
.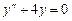 .
.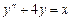 .
.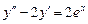 .
.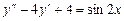 .
.
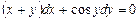 ; б)
; б)  ;
в)
;
в) 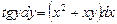 ; г)
; г) 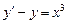 .
.
 ; б)
; б) 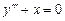 ; в)
; в) 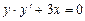 ; г)
; г) 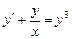 .
.
 ; б)
; б)  ; в)
; в) 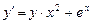 ; г)
; г) 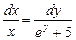 .
.
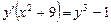 является
а) дифференциальным уравнением второго порядка;
б)диф. уравнением с разделяющимися переменными;
в) линейным дифференциальным уравнением;
г) однородным дифференциальным уравнением.
является
а) дифференциальным уравнением второго порядка;
б)диф. уравнением с разделяющимися переменными;
в) линейным дифференциальным уравнением;
г) однородным дифференциальным уравнением.
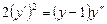 решается с помощью замены
a)
решается с помощью замены
a) 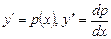 ; б)
; б) 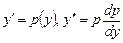 ;
в)
;
в) 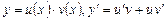 ; г)
; г) 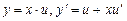 .
.
 .
.
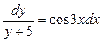 имеет вид
а)
имеет вид
а)  ; б)
; б) 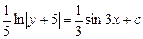 ;
в)
;
в) 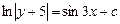 ; г)
; г)  .
.
 дифференциального уравнения
дифференциального уравнения  ищется в виде
а)
ищется в виде
а) 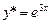 ; б)
; б) 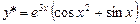 ;
в)
;
в)  ; г)
; г) 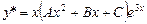 .
.
 – числовая после-довательность. Выражение вида
– числовая после-довательность. Выражение вида
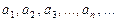 – членами ряда, а число
– членами ряда, а число 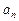 –
– 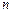 -м членом ряда.
-м членом ряда.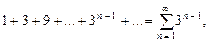
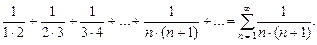
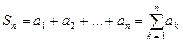
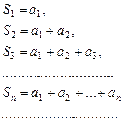
 частичных сумм ряда
частичных сумм ряда
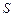 – суммой данного ряда:
– суммой данного ряда:
 не существует или равен бесконечности, то ряд называют расходящимся.
не существует или равен бесконечности, то ряд называют расходящимся.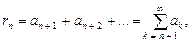
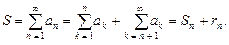
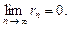
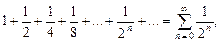
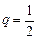 . Вычислим n -ю частичную сумму этого ряда:
. Вычислим n -ю частичную сумму этого ряда: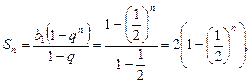
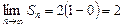 .
.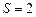 .
. является расходящимся, т.к.
является расходящимся, т.к.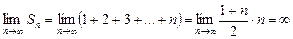 .
.


