
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 9. Дифференциальные уравненияСодержание книги
Поиск на нашем сайте
1. Обыкновенные дифференциальные уравнения: порядок уравне-ния, общее и частное решение, общий и частный интеграл. [1] т.2, часть IV, раздел 2, § 1, 2. 2. Дифференциальные уравнения первого порядка. Задача Коши. [1] т.2, часть IV, раздел 2, § 1, 2. 3. Дифференциальные уравнения с разделяющимися переменными. [1] т.2, часть IV, раздел 2, § 1, 2. 4. Однородные дифференциальные уравнения первого порядка. [1] т.2, часть IV, раздел 2, § 1, 2. 5. Линейные дифференциальные уравнения первого порядка. [1] т.2, часть IV, раздел 2, § 1, 2.
Вопросы, отмеченные символом э, изучаются только студентами агроэнергетического факультета БГАТУ. 6. Уравнение Бернулли. [1] т.2, часть IV, раздел 2, § 1, 2. 7. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка. [1] т.2, часть IV, раздел 2, § 3. 8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. [1] т.2, часть IV, раздел 2, § 3. 9. Линейные неоднородные дифференциальные уравнения 2-го порядка со специальной правой частью.[1] т.2, часть IV, раздел 2, § 4, 5, 6, 7. 10э.Системы линейных дифференциальных уравнений. [1] т.2, часть IV, раздел 2, § 10.
Модуль 10. Ряды 1. Понятие числового ряда и его суммы. [1] т.1, часть II, § 20. 2. Необходимый признак сходимости числового ряда. Гармоничес-кий ряд. [1] т.1, часть II, § 20. 3. Достаточные признаки сходимости числовых рядов: признак сравнения, призак Д´Аламбера, радикальный признак Коши, интегральный призак Коши. [1] т.1, часть II, § 20. 4. Знакопеременные ряды. Признак Лейбница о сходимости знако-чередующегося ряда. [1] т.1, часть II, § 20. 5. Абсолютно сходящиеся ряды и их свойства. [1] т.1, часть II, § 20. 6. Степенной ряд. Теорема Абеля. [1] т.1, часть II, § 21. 7. Радиус и область сходимости степенного ряда.[1]т.1,частьII, § 21. 8. Формулы Тейлора и Маклорена. [1] т.1, часть II, § 22. 9. Ряды Тейлора и Маклорена. Условия разложимости функции в степенной ряд. [1] т.1, часть II, § 22. 10. Степеные ряды элементарных функций. [1] т.1, ч.II,§ 22. 11. Биноминальный ряд. [1] т.1, часть II, § 22. 12. Приложения рядов к приближенным вычислениям. [1] т.1, часть II, § 22. 13э.Тригонометрический ряд. Ряд Фурье для функции с периодом 14э.Ряды Фурье для четной и нечетной функций.[1] т.1, часть II, §23. 15э.Ряд Фурье для функции с периодом 16э.Разложение в ряд Фурье непериодических функций, заданных на отрезке. [1] т.1, часть II, § 23. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Высшая математика для инженеров: В 2 т.Т.1,2: учеб. пособие для вузов/ С.А.Минюк, В.И.Булгаков, А.В.Метельский, З.М.Наркун; подобщ.ред.Н.А.Микулика.–н.:ОООЭлайда»,2004. 2. Гусак, А.А.Высшая математика: Т.2. – Мн.: Тетра Системс, 2006. 3. Сборник индивидуальных заданий по высшей математике:В.4 ч.: учеб. пособие / под ред. А.П. Рябушко. – Мн.: Выш. школа, 2007. 4. Пискунов, Н.С. Дифференциальное и интегральное исчисление: Т. 1, 2 / Н.С. Пискунов. – М.: Наука, 1985. 5. Бермант, А.Ф. Краткий курс математического анализа / А.Ф. Бермант, И.Г. Араманович. – М.: Наука, 1985. 6. Высшая математика в упражнениях и задачах: Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – Мн.: Выш. школа, 1986. 7. Общий курс высшей математики/Р.М.Жевняк[и др.]– Орша,1996 8. Бугров, Я.С. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1989. 9. Лихолетов, И.И. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике / И.И. Лихолетов, И.П. Мацкевич. – Мн.: Выш. школа, 1976. 10. Комплексные числа и их применение в электротехнике. Методические указания и задания для агроэнергетических специальностей БГАТУ. Мн.: БГАТУ, 2002. Модуль 8. КОМПЛЕКСНЫЕ ЧИСЛА Определение и геометрическое изображение Комплексного числа Попытки решения квадратных уравнений с отрицательным дискриминантом привели к возникновению понятия комплексных чисел. Комплексным числом называется число вида
где В технической литературе используют обозначение Число х называется действительной частью комплексного числа, а у – его мнимой частью и обозначают Запись Множество всех комплексных чисел обозначают С. При При Два комплексных числа равны, если равны их действительные и мнимые части. Числа
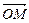 . И наоборот, каждая точка М (х, у) плоскости изображает комплексное число . И наоборот, каждая точка М (х, у) плоскости изображает комплексное число 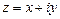 (рис. 8.1). (рис. 8.1).
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |


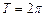 . Теорема о разложимости периодической функции в ряд Фурье. [1] т.1, часть II, § 23.
. Теорема о разложимости периодической функции в ряд Фурье. [1] т.1, часть II, § 23.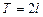 . [1] т.1, часть II, § 23.
. [1] т.1, часть II, § 23.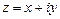 , (8.1)
, (8.1)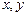 – действительные числа,
– действительные числа, 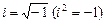 – мнимая единица.
– мнимая единица.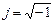 .
.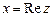 ,
, 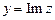 .
.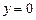 получим действительное число
получим действительное число  , т.е. RÌ C.
, т.е. RÌ C.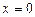 получим число вида
получим число вида 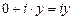 , которое называется чисто мнимым.
, которое называется чисто мнимым.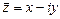 называются сопряженными.
называются сопряженными.



