
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности. Формула БайесаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть событие А может наступить при условии появления одного из несовместных событий
которая носит название формулы полной вероятности. Пример 14.10. В мастерской работают 5 станков 1-го типа, 3 станка 2-го типа и 2 станка 3-го типа. Детали, изготовленные на этих станках, могут быть различного качества. Станки 1-го типа дают 94% качественных деталей, станки 2-го типа дают 90% качественных деталей, а станки 3-го типа - 85% качественных деталей. Найти вероятность того, что взятая наугад деталь качественная. Решение. Пусть событие А – взятая деталь качественная. Выдвигаем следующие гипотезы: Н 1 – деталь изготовлена станком 1-го типа; Н 2 – деталь изготовлена станком 2-го типа; Н 3 – деталь изготовлена станком 3-го типа. По формуле полной вероятности имеем:
По условию задачи
где Подставляем числовые значения в формулу полной вероятности и получаем:
Формула Байеса (вероятности гипотез). Пусть событие А может наступить при условии появления одного из несовместных событий
Пример 14.11. В трех ящиках находятся одинаковые детали. В 1-ом – 10 деталей, из них 3 нестандартных, во 2-ом –15 деталей, из них 5 нестандартных, в 3-ем – 20 деталей, из них 6 нестандартных. Из одного из ящиков извлечена деталь, которая оказалась нестандартной. Определить вероятность того, что деталь извлечена из 2-го ящика. Решение. Основное событие А – извлечена нестандартная деталь. Вводим гипотезы:
По формуле Байеса следует найти
где Гипотезы равновозможные, следовательно,
По условию задачи условные вероятности события А равны:
Тогда
Повторение испытаний Формула Бернулли. Если в каждом из
На практике формулой Бернулли удобно пользоваться, если Пример 14.12. Вероятность изготовления на станке детали высшего качества равна 0,8. Найти вероятность того, что из 6 взятых наудачу деталей 4 высшего качества. Решение. Из условия задачи имеем, что n = 6, m = 4, p = 0,8, q = 1-0,8 = 0,2. Тогда, применяя формулу Бернулли, получаем
Формула Пуассона. Если производится достаточно большое число испытаний (
Пример 14.13. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что изделие в пути повредится Решение. Применяем формулу По данным задачи Тогда Локальная теорема Лапласа. Если производится
где Функция Значения функции Замечание. В таблице 3 приведены значения функции Пример 14.14. Производятся 400 независимых испытаний. Вероятности наступления события А в каждом испытании Решение. По условию задачи имеем:
Из таблицы 3 находим значение функции
Интегральная теорема Лапласа. Если вероятность
где Функция Пример 14.15. Вероятность оказаться стандартным для данного изделия 0,8. Найти вероятность того, что среди 900 изделий число стандартных будет находиться в границах от 690 до 740. Решение. По условию задачи: п = 900, т1 = 690, т2 = 740. Применяя интегральную теорему Лапласа, получаем
Находим значения функции
Тогда Определение. Наивероятнейшим числом Наивероятнейшее число определяется по формуле
где
Пример 14.16. При данном технологическом процессе 85% продукция высшего качества. Найти наивероятнейшее число изделий высшего качества среди 150 изделий. Решение. По условию задачи
Пример 14.17. Вероятность попадания в мишень для стрелка равна Решение. По условию задачи
Случайные величины
Определение. Случайной называется величина, которая в результате опыта может принять одно и только одно возможное значение, неизвестно заранее, какое именно. Например, посеяно 100 зерен пшеницы для определения ее всхожести. Число взошедших зерен есть случайная величина, которая может принять одно из значений: 0, 1, 2, …, 100. Определение. Случайная величина называется дискретной, если она принимает отдельные, изолированные друг от друга возможные значения, которые можно перенумеровать. Число взошедших зерен пшеницы есть дискретная случайная величина. Определение. Непрерывной случайной величиной называется такая случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток, конечный или бесконечный. Например, расстояние, которое пролетит снаряд при выстреле из орудия, есть непрерывная случайная величина. Возможные зна-чения этой величины принадлежат некоторому промежутку Случайные величины обозначаются: Определение. Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Для дискретной случайной величины закон распределения можно задать в виде таблицы
Определение. Интегральной функцией распределения случайной величины
Свойства интегральной функции 1. Значения интегральной функции принадлежат отрезку
2. 3. 4. Вероятность того, что случайная величина
5. Вероятность того, что непрерывная случайная величина
Определение. Дифференциальной функцией распределения или плотностью распределения вероятностей случайной величины Обозначается плотность вероятности через
Так как Таким образом, если существует Интегральная функция выражается через дифференциальную формулой:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.72.220 (0.006 с.) |

 ,
,  , …
, …  , образующих полную группу. Будем эти события называть гипотезами. Вероятность события А в этом случае вычисляется по формуле
, образующих полную группу. Будем эти события называть гипотезами. Вероятность события А в этом случае вычисляется по формуле ,
,
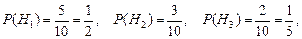
 .
. ,
,  - условные вероятности, что взятая деталь качественная, если она изготовлена на станке i -го типа.
- условные вероятности, что взятая деталь качественная, если она изготовлена на станке i -го типа.
 , …,
, …,  , образующих полную группу. Вероятности этих гипотез до опыта известны и соответственно равны
, образующих полную группу. Вероятности этих гипотез до опыта известны и соответственно равны  ,
,  , …
, …  . Произведен опыт, в результате которого наступило событие А. Вероятность
. Произведен опыт, в результате которого наступило событие А. Вероятность  гипотезы
гипотезы  , после того, как событие А наступило, определяется по формуле Байеса
, после того, как событие А наступило, определяется по формуле Байеса ,
,  .
. - деталь извлечена из 3-го ящика.
- деталь извлечена из 3-го ящика. , т.е.
, т.е. ,
, .
.
 .
.
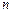 независимых испытаний вероятность появления события А постоянна и равна
независимых испытаний вероятность появления события А постоянна и равна  , то вероятность того, что в
, то вероятность того, что в 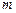 раз, определяется по формуле Бернулли
раз, определяется по формуле Бернулли , где
, где  .
. .
. .
. испытаниях событие А наступит
испытаниях событие А наступит  , где
, где  .
.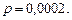 Найти вероятность того, что в пути повредится только 3 изделия.
Найти вероятность того, что в пути повредится только 3 изделия. ,
, 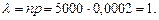

 ,
, ,
,  , причем результат тем точнее, чем ближе значение
, причем результат тем точнее, чем ближе значение  и чем больше
и чем больше  – четная. Это означает, что
– четная. Это означает, что  .
. , при
, при  полагают
полагают 
 Найти вероятность того, что в 400 испытаниях событие А наступит 100 раз.
Найти вероятность того, что в 400 испытаниях событие А наступит 100 раз. , q = 1-0,2 = 0,8, n = 400, m =100. Тогда, применяя локальную теорему Лапласа, находим
, q = 1-0,2 = 0,8, n = 400, m =100. Тогда, применяя локальную теорему Лапласа, находим .
. Тогда
Тогда
 раз и не более чем
раз и не более чем  раза, определяется по формуле
раза, определяется по формуле ,
, ,
,  ,
,  .
. - нечетная. Это означает
- нечетная. Это означает  .Значения функции
.Значения функции  полагают
полагают 
 , где
, где и
и  .
.
 .
.
 появления события А в
появления события А в 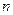 независимых испытаниях называется число, для которого вероятность
независимых испытаниях называется число, для которого вероятность  превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытаний.
превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытаний. ,
,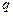 - вероятность не наступления события А в одном испытании,
- вероятность не наступления события А в одном испытании, . Подставим эти значения в формулу для нахождения наивероятнейшего числа и решим неравенство
. Подставим эти значения в формулу для нахождения наивероятнейшего числа и решим неравенство ,
, ,
,
 . Определить наивероятнейшее число попадания при 13 выстрелах.
. Определить наивероятнейшее число попадания при 13 выстрелах. . Тогда, подставляя эти значения в формулу для нахождения наивероятнейшего числа, получаем
. Тогда, подставляя эти значения в формулу для нахождения наивероятнейшего числа, получаем ,
, Þ
Þ  или
или  .
. .
. ,
,  ,
,  и т.д.
и т.д. – возможные значения случайной величины
– возможные значения случайной величины 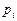 – соответствующие им вероятности.
– соответствующие им вероятности. , выражающая вероятность того, что случайная величина
, выражающая вероятность того, что случайная величина  :
:
 :
: .
. , если
, если 


 , равна приращению интегральной функции на этом интервале:
, равна приращению интегральной функции на этом интервале:
 Поэтому для непрерывной случайной величины справедлива формула
Поэтому для непрерывной случайной величины справедлива формула
 называется отношение вероятности попадания непрерывной случайной величины на элементарный участок от
называется отношение вероятности попадания непрерывной случайной величины на элементарный участок от  к длине этого участка, когда
к длине этого участка, когда 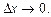
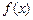 . По определению имеем:
. По определению имеем: .
. , то
, то  .
. , то существует и
, то существует и  .
.


