
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Максвелла-Мора. Техніка обчислення переміщень.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Найзагальнішим методом обчислення переміщень у стержневих системах є метод Мора. Він випливає з принципу можливих переміщень і дає можливість визначити переміщення точок системи через зусилля в її елементах. Принцип можливих переміщень, який сформульовано Лагранжем для систем, складених з тіл, що не деформуються, є фундаментальним принципом механіки. Згідно з цим принципом для будь-якої зрівноваженої системи сума робіт всіх прикладених зовнішніх сил на віртуальних переміщеннях дорівнює нулю. Для пружних систем означений принцип може бути сформульований таким чином: в будь-якій пружній зрівноваженій системі сума робіт всіх зовнішніх і внутрішніх сил на будь-яких можливих нескінченно малих переміщеннях дорівнює нулю, тобто А+U=0 (1). У цьому виразі А- робота зовнішніх, а U- внутрішніх сил. Зовнішні сили – це навантаження, прикладенні до конструкції, та опорні реакції, внутрішні – це зусилля, які виникають в елементах споруди при її деформуванні. Можливими вважаються переміщення, які пропускаються наявними в’язями. Розглянемо два напружено-деформовані стани стержневої системи. Перший стан зумовлено зовнішніми навантаженнями, які, по суті, можуть бути довільними. Назвемо цей напружено-деформований стан стержневої системи вантажним, або станом Р. У другому стані на стержневу систему вздовж деякої довільної прямої і-і діє одна зосереджена сила, яка дорівнює одиниці. Такий стан (стан і) будемо називати допоміжним, або одиничним. Обидва ці стани є можливими і, згідно з принципом Лагранжа, сума робіт одного стану на переміщеннях іншого має дорівнювати нулю. Розглянемо можливу роботу сил стану і на переміщення стану Р: Аір+Uір=0 (2). Можлива робота зовнішніх сил дорівнює добутку одиничної сили стану і на відповідне переміщення стану Р: Аір= 1·▲ір. (3). Можлива робота внутрішніх сил: Uip=-∑ ▲ір=∑ ℇр= ▲ір=∑
Застосування формули Максвелла-Мора для різних розрахункових схем.
Величини кожного з трьох доданків у формулі Максвелла–Мора характеризують внесок того чи іншого виду внутрішніх зусиль в переміщення, що розшукується. На підставі аналізу цих доданків можна дійти висновку, що для різного виду конструкцій нехтування деякими видами зусиль мало позначається на величині переміщення. Так, для балок і рам, деформування яких відбувається переважно за рахунок згину, можна знехтувати впливом поздовжніх і поперечних сил. У такому разі формула Максвелла–Мора матиме вигляд:
Співвідношення (3.24) називають інтегралом Мора. Для ферм, в стержнях яких існують поздовжні деформації, можна записати:
Для арок:
Правило Верещагіна За правилом Верещагіна для обчислення інтеграла \MjMpdx достатньо помножити площу епюри
епюр (рис.3.9), одна з яких
Інтеграл у правій частині співвідношення - це статичний момент Sp площі епюри
Необхідно звернути увагу: • принаймні одна з епюр, які перемножуються, має бути прямолінійною; • ордината уі повинна бути взята на прямолінійній епюрі.
Формула Сімпсона–Корноухова
При використанні формули Сімпсона–Корноухова необхідно, щоб обидві перемножувані епюри не мали зламів, розривів та точок перегину. В противному разі інтервал інтегрування треба розкласти на окремі підінтервали. Приклад 3.1. Обчислити кут повороту в перерізі k рами (рис.3.11,а).
1. Визначення зусилля від зовнішнього навантаження. На ригелі: M p = P(a - x), на стійці Mp = Pa. Епюру Mp побудовано на рис.3.11,б. 2. Створення допоміжного стану. Допоміжний стан (стан i) зображено на рис.3.11,в. 3. Визначення зусиль в допоміжному стану: на ригелі Mi = 1, на стояку Mi = 1. Епюру Mi побудовано на рис.3.11,г.
4. Обчислення переміщення за формулою Мора.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.80 (0.007 с.) |

 (4) Підставимо роботу зовнішніх сил (3) і можливу роботу внутрішніх сил (4) у співвідношення (2). Маємо:
(4) Підставимо роботу зовнішніх сил (3) і можливу роботу внутрішніх сил (4) у співвідношення (2). Маємо: , kp=
, kp=  =
=  , Ɣp=
, Ɣp=  , (6), де ŋ- безрозмірний коефіцієнт, що залежить від форми перерізу стержня і обчислюються за формулою: ŋ=А
, (6), де ŋ- безрозмірний коефіцієнт, що залежить від форми перерізу стержня і обчислюються за формулою: ŋ=А  (7). (Зокрема, для прямокутного перерізу ŋ=1,2). З урахуванням (6).
(7). (Зокрема, для прямокутного перерізу ŋ=1,2). З урахуванням (6). (8). Цей вираз називається формулою Максвелла-Мора, або інтегралом Мора. За допомогою цієї формули можна обчислити будь-яке переміщення в будь-якій стержневій системі через внутрішні зусилля двох її станів.
(8). Цей вираз називається формулою Максвелла-Мора, або інтегралом Мора. За допомогою цієї формули можна обчислити будь-яке переміщення в будь-якій стержневій системі через внутрішні зусилля двох її станів. (3.24)
(3.24) (3.25)
(3.25)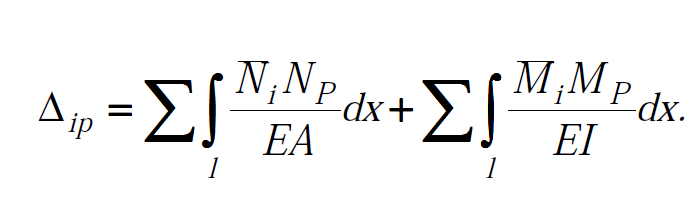
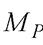 I на ординату епюри,
I на ординату епюри,  що береться під центром тяжіння епюри
що береться під центром тяжіння епюри  (рис.3.8):
(рис.3.8): Якщо ордината yt i площа А розташовані по один і той самий бік стержня, добуток береться зі знаком "плюс". Насправді, розглянемо обчислення інтеграла
Якщо ордината yt i площа А розташовані по один і той самий бік стержня, добуток береться зі знаком "плюс". Насправді, розглянемо обчислення інтеграла на прикладі перемножения двох
на прикладі перемножения двох мае довільний характер, а друга -обмежена
мае довільний характер, а друга -обмежена  прямою. Добуток
прямою. Добуток  є елементарною площею, яка береться на епюрі
є елементарною площею, яка береться на епюрі 

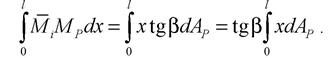 Ординату на прямолінійній епюрі можна представити у вигляді Мі = xtg(3. Зрештою інтеграл набуває вигляду:
Ординату на прямолінійній епюрі можна представити у вигляді Мі = xtg(3. Зрештою інтеграл набуває вигляду: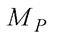 стосовно осі у\, яка проходить через точку перетину епюри
стосовно осі у\, яка проходить через точку перетину епюри  з прямою, що збігається з віссю стержня. Як відомо, статичний момент площі дорівнює добутку площі на координату центра її тяжіння
з прямою, що збігається з віссю стержня. Як відомо, статичний момент площі дорівнює добутку площі на координату центра її тяжіння 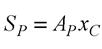 . На цій під ставі маємо
. На цій під ставі маємо
 I нарешті, помітивши, що
I нарешті, помітивши, що  остаточно одержуємо:
остаточно одержуємо: – це окремий випадок відомої з математичного аналізу формули Сімпсона (формули парабол) для обчислення визначених інтегралів, коли інтервал інтегрування розкладається на дві ділянки (рис.3.10):
– це окремий випадок відомої з математичного аналізу формули Сімпсона (формули парабол) для обчислення визначених інтегралів, коли інтервал інтегрування розкладається на дві ділянки (рис.3.10):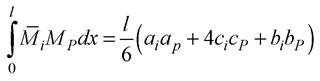
 Процес розв’язання містить чотири етапи:
Процес розв’язання містить чотири етапи:



