
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Припущення будівельної механікиСодержание книги Поиск на нашем сайте
Припущення будівельної механіки Розрахунки в будівельній механіці базуються на деяких припущеннях і гіпотезах. Вони збігаються з припущеннями і гіпотезами опору матеріалу, але повинні бути віднесені до всієї споруди в цілому. Для побудови теорії опору матеріалів приймаються деякі гіпотези і принципи відповідно до структури і властивостей матеріалів, характеру деформацій і напружень, а також діючих сил і геометрії конструкцій. · Гіпотеза про суцільність матеріалу. Тіло вважається суцільним, тобто неперервним до деформації залишається неперервним і після деформації (без порожнин, розривів). · Гіпотеза про однорідність і ізотропність матеріалу. При цьому вважають, що властивості тіла в будь-якій точці і в будь-якому напрямку однакові. · Гіпотези плоских перерізів. Плоскі перерізи, проведені в тілі до деформації, залишаються плоскими і після деформації. Вони залишаються нормальними до осі стержня в процесі деформації. Ця гіпотеза виправдовується дослідом в тому випадку, коли тіло має продовжену форму (стрижень, брус). Цю гіпотезу також називають гіпотезою Бернуллі · Гіпотеза про ідеальну пружність і лінійну залежність між напруженнями і деформаціями. Ідеальна пружність — здатність тіла, яке здобуло деформацію, після усунення причин, що спричиняли її, повністю відновити свою початкову форму. · Принцип Сен-Венана. В точках тіла, достатньо віддалених від місця прикладання зовнішніх сил, внутрішні зусилля (напруження) дуже мало залежать від способу прикладання цих сил. Такий принцип дозволяє замінити одну систему сил статично їй еквівалентною (переміщення сил з верхньої частини балки на нижню, заміна зосередженої сили на групу розподілених і навпаки).Інколи принцип Сен-Венана формулюють таким чином: Поблизу місць прикладення навантажень формули опору матеріалів недійсні. · Принцип незалежності дії сил (суперпозиції). Ефект від суми впливу дорівнює сумі ефектів від окремого впливу. Згідно з цим принципом переміщення, напруження і деформації навантаженого тіла вважають незалежними від порядку прикладання сил.
Кількісний етап кінематичного аналізу З погляду кінематичного аналізу кожна споруда складається з дисків і матеріальних точок. Кількісний етап має за мету визначення кількості ступенів вільності всієї розрахункової схеми, тобто сумарної кількості ступнів вільності,які визначають положення елементів системи відносно якоїсь нерухомої системи координат.Цю величину називають ступенем геометричної змінюваності системи.Виходячи з викладених кінематичних властивостей елементів розрахункової споруди,можна записати формулу(Чебишева) для визначення ступня геометричної змінюваності «Г» с-ми: Г=3Д+2В-3П-2Ш-С-3 де Д- кількість простих дисків; В-кількість вузлів в’язей; П-к-ть припайок; Ш-простих шарнірів; С-простих в’язей; 3-число ступнів вільності всієї плоскої розрахункової схеми як твердого тіла в її площині. Ступінь геометричної змінюваності розрахункової схеми,обчислену за формулою,дає змогу визначити її кінематичну характеристику.
Якщо Г›0,розрахункова схема споруди безперечно є геометрично змінюваною. Цей результат засвідчує, що з’єднувальних пристроїв не вистачає для усунення можливості переміщень,які можуть робити окремі елементи системи або вся ця система в цілому. Якщо Г≤0,можна стверджувати,що виконується необхідна умова геометричної незмінюваності розрахункової схеми,бо з’єднувальні пристрої можуть забезпечити нерухомість усих елементів і систем вцілому. Проте з’єднувальні пристрої можуть бути встановлені в такий спосіб,що в однах зонах конструкції кількість їх надмірна,а в інших- недостатня. У деяких випадках особливе розташування з’єднувальних пристроїв може приводити до появи миттєвого центра взаємного обертання елементів системи. Таким чином при Г≤0 розрахункова схема може бути або геом. Незмінюваною, або геом..змінюваною, або нарешті, миттєво змінюваною залежно від розташування дисків і зєднань. Належність до конкретного типу остаточно встановлюється на підставі виконання якісного етапу аналізу розрахункової схеми.
Спосіб вирізання вузлів при розрахунку плоских ферм Розрахунок ферми способом вирізання вузлів доцільно проводити у такій послідовності: Розв’язують рівняння рівноваги і знаходять невідомі зусилля. Недоліком способу вирізання вузлів є те, що помилки у обчисленнях зусиль або похибки заокруглення впливають на наступні розрахунки. Тому цей спосіб доцільно застосовувати лише для розрахунку двостержневих вузлів та вузлів, що належать до окремих випадків рівноваги. У деяких окремих випадках рівноваги вузлів для визначення зусиль у стержнях можна не складати рівняння рівноваги вузлів. Класифікація плоских рам Рамою назив. Систему, що складається з прямолінійних стержнів, які поєднуються між собою у вузлах. При розрахунку рам доцільно розподілити їх за якимось ознаками. Для цього зручно скористатись ознаками кінематичного аналізу. Всю сукупність плоских рам можна розділити на прості і складені. До простих можна віднести рами, для яких структурний аналіз здійснюється за один етап, тобто такі, що утворюються з двох або трьох дисківза допомогою звичайних способів з”эднання дисків. Прості в свою чергу діляться на: консольні, балкові,аркові. До консольних рам можна віднести такі, що є приєднанням двох дисків, одним із яких є диск „земля”, за допомогою припайки. Балкові рами утворюються з двох дисків за способом Шухова або за способои Полонсо. Рами. Що утворені за способом шарнірного трикутника можуть відноситись до аркового типу.
До складених рам можна віднести ті, для яких структурний етап кінематичного аналізу здійснюється більше ніж за один етап. Частину складеної рами, що відповідає одному етапу, умовно назив. „поверхом”. Отже кожен поверх може розглядатись як проста рама і тому складену раму можна розглядати як сукупність кількох простиз рам.
Продовженя дал
Продовження питання 22 Універсальні позначення переміщень дорівнює одиниці. В позначення вводяться два індекси, наприклад На рис.3.4,а-в зображено три деформованих стани балки, що перебуває під дією різних навантажень.
повороту, від дії сили
Правило Верещагіна За правилом Верещагіна для обчислення інтеграла \MjMpdx достатньо помножити площу епюри
епюр (рис.3.9), одна з яких
Інтеграл у правій частині співвідношення - це статичний момент Sp площі епюри
Необхідно звернути увагу: • принаймні одна з епюр, які перемножуються, має бути прямолінійною; • ордината уі повинна бути взята на прямолінійній епюрі.
Формула Сімпсона–Корноухова
При використанні формули Сімпсона–Корноухова необхідно, щоб обидві перемножувані епюри не мали зламів, розривів та точок перегину. В противному разі інтервал інтегрування треба розкласти на окремі підінтервали. Приклад 3.1. Обчислити кут повороту в перерізі k рами (рис.3.11,а).
1. Визначення зусилля від зовнішнього навантаження. На ригелі: M p = P(a - x), на стійці Mp = Pa. Епюру Mp побудовано на рис.3.11,б. 2. Створення допоміжного стану. Допоміжний стан (стан i) зображено на рис.3.11,в. 3. Визначення зусиль в допоміжному стану: на ригелі Mi = 1, на стояку Mi = 1. Епюру Mi побудовано на рис.3.11,г.
4. Обчислення переміщення за формулою Мора. Лінії впливу у фермах
38. Лінії впливу в шпренгельних фермах У ферми, що мають великі відстані між вузлами вантажного поясу, часто вводять додаткові вузлі, на які спиратимуться поперечні балки, що несуть навантаження від покриття або від проїжджої частини мостів. Для збереження геометричної незмінюваності водночас із вузлами вводять додаткові стержні, які називаються шпренгельиими стержнями. Ферми, які містять додаткові вузли вантажного поясу та відповідні ним додаткові стержні, називають шпренгельиими фермами.З точки зору геометричної структури шпренгельну ферму можна розглядати як таку, що складається з основної ферми, в панелі якої введено додаткові трикутні ферми, які спираються на вузли основної ферми. Такі додаткові однопанельні ферми називаються шпренгеля-ми. Навантаження на шпренгелі здійснюється лише силами, прикладеними в додаткових вузлах поясу. Якщо ці вузли не навантажені, то зусилля у відповідному шпренгелі відсутні. Таким чином, шпренгелі працюють лише на локальне навантаження панелей основної ферми.Деякі типові види шпренгелів розглянемо на прикладі шпренгель-ної ферми (рис. 8.11,а).Ферму можна розглядати як основну ферму з паралельними поясами 1-2-3-4-5-6 та Г-?-У-4'-У-Є, в панелі якої вставлено додаткові вузли, трикутні шпренгелі та додаткові стійки, через які навантаження передається на шпренгелі (рис. 8.11,6). Схеми шпренгелів представлено на рис. 8.11,в.Шпренгель, який введено у першу панель, спирається на вузли 1 і 2 основної ферми. Завантажується шпренгель через додаткову стійку 7-7. Навантаження з додаткового вузла 7 верхнього поясу через опорні реакції шпренгеля передаються на вузли 1 і 2 знов-таки верхнього поясу. Такого типу шпренгелі називаються одноярусними.Шпренгель, введений в другу панель, спирається на вузли 2' і З' нижнього поясу. Через стійку 8-8* навантаження з додаткового вузла 8, який розташовано в верхньому поясі, через шпренгель передається на вузли нижньго поясу основної ферми. Шпренгелі такого типу називаються двоярусними. Усі стержні шпренгельної ферми можна поділити на 4 категорії (рис. 8.Па): Стержні які відносяться лише до основної ферми. Наприклад, 2-8, 8-3, 2-8', 34' тощо. Стержні, які належать лише шпреигелям та додаткові стійки, через які шпренгелі навантажуються (2-7', 7-7', 2'-8\ 8-8' тощо). Стержні, які водночас належать як основній фермі, так і шпрен-гелю (1-7, 7-2, ЩШ 9'-10" тощо). Стійки основної ферми, якщо принаймні в одній, суміжній зі стійкою, панелі введено двоярусний шпренгель. Наприклад, 2-21,3-3', 4-4', 5-5', але не стійка 1-Г, бо в першій панелі, з якою межує зазначений стержень, немає двоярусного шпренгеля. Це стержень першої категорії.
Припущення будівельної механіки Розрахунки в будівельній механіці базуються на деяких припущеннях і гіпотезах. Вони збігаються з припущеннями і гіпотезами опору матеріалу, але повинні бути віднесені до всієї споруди в цілому. Для побудови теорії опору матеріалів приймаються деякі гіпотези і принципи відповідно до структури і властивостей матеріалів, характеру деформацій і напружень, а також діючих сил і геометрії конструкцій. · Гіпотеза про суцільність матеріалу. Тіло вважається суцільним, тобто неперервним до деформації залишається неперервним і після деформації (без порожнин, розривів). · Гіпотеза про однорідність і ізотропність матеріалу. При цьому вважають, що властивості тіла в будь-якій точці і в будь-якому напрямку однакові. · Гіпотези плоских перерізів. Плоскі перерізи, проведені в тілі до деформації, залишаються плоскими і після деформації. Вони залишаються нормальними до осі стержня в процесі деформації. Ця гіпотеза виправдовується дослідом в тому випадку, коли тіло має продовжену форму (стрижень, брус). Цю гіпотезу також називають гіпотезою Бернуллі · Гіпотеза про ідеальну пружність і лінійну залежність між напруженнями і деформаціями. Ідеальна пружність — здатність тіла, яке здобуло деформацію, після усунення причин, що спричиняли її, повністю відновити свою початкову форму. · Принцип Сен-Венана. В точках тіла, достатньо віддалених від місця прикладання зовнішніх сил, внутрішні зусилля (напруження) дуже мало залежать від способу прикладання цих сил. Такий принцип дозволяє замінити одну систему сил статично їй еквівалентною (переміщення сил з верхньої частини балки на нижню, заміна зосередженої сили на групу розподілених і навпаки).Інколи принцип Сен-Венана формулюють таким чином: Поблизу місць прикладення навантажень формули опору матеріалів недійсні. · Принцип незалежності дії сил (суперпозиції). Ефект від суми впливу дорівнює сумі ефектів від окремого впливу. Згідно з цим принципом переміщення, напруження і деформації навантаженого тіла вважають незалежними від порядку прикладання сил.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.235.107 (0.009 с.) |

 Індекси позначають місцезнаходження і характер переміщення, а також дію, що його зумовлює. Перший індекс пов’язаний з характером та напрямом переміщення. Він вказує на узагальнену силу, яка відповідає цим характеристикам. Другий індекс пов’язаний із дією, яка викликає це переміщення.
Індекси позначають місцезнаходження і характер переміщення, а також дію, що його зумовлює. Перший індекс пов’язаний з характером та напрямом переміщення. Він вказує на узагальнену силу, яка відповідає цим характеристикам. Другий індекс пов’язаний із дією, яка викликає це переміщення. Так,
Так,  являє собою переміщення в напрямі сили
являє собою переміщення в напрямі сили  першого стану, тобто прогин балки, від дії сили
першого стану, тобто прогин балки, від дії сили  другого стану;
другого стану;  - переміщення в напрямі сили третього
- переміщення в напрямі сили третього  стану, тобто кут
стану, тобто кут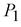 першого стану тощо. І взагалі можна сказати, що
першого стану тощо. І взагалі можна сказати, що  - це переміщення в напрямі узагальненої сили стану i від дії узагальненої сили стану
- це переміщення в напрямі узагальненої сили стану i від дії узагальненої сили стану  Отже, для того щоб позначити будь-яке переміщення, необхідно створити допоміжний стан конструкції, приклавши узагальнену силу, яка відповідає переміщенню. Так, для того, щоб позначити в попередньому прикладі вертикальне переміщення точки k від дії сил стану 1, створимо допоміжний стан k, приклавши в перерізі k балки вертикальну зосереджену силу (рис.3.4,г). Тоді дане переміщення позначатиметься
Отже, для того щоб позначити будь-яке переміщення, необхідно створити допоміжний стан конструкції, приклавши узагальнену силу, яка відповідає переміщенню. Так, для того, щоб позначити в попередньому прикладі вертикальне переміщення точки k від дії сил стану 1, створимо допоміжний стан k, приклавши в перерізі k балки вертикальну зосереджену силу (рис.3.4,г). Тоді дане переміщення позначатиметься 
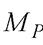 I на ординату епюри,
I на ординату епюри,  що береться під центром тяжіння епюри
що береться під центром тяжіння епюри  (рис.3.8):
(рис.3.8): Якщо ордината yt i площа А розташовані по один і той самий бік стержня, добуток береться зі знаком "плюс". Насправді, розглянемо обчислення інтеграла
Якщо ордината yt i площа А розташовані по один і той самий бік стержня, добуток береться зі знаком "плюс". Насправді, розглянемо обчислення інтеграла на прикладі перемножения двох
на прикладі перемножения двох мае довільний характер, а друга -обмежена
мае довільний характер, а друга -обмежена  прямою. Добуток
прямою. Добуток  є елементарною площею, яка береться на епюрі
є елементарною площею, яка береться на епюрі 

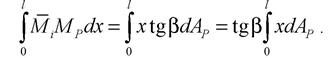 Ординату на прямолінійній епюрі можна представити у вигляді Мі = xtg(3. Зрештою інтеграл набуває вигляду:
Ординату на прямолінійній епюрі можна представити у вигляді Мі = xtg(3. Зрештою інтеграл набуває вигляду: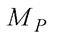 стосовно осі у\, яка проходить через точку перетину епюри
стосовно осі у\, яка проходить через точку перетину епюри  з прямою, що збігається з віссю стержня. Як відомо, статичний момент площі дорівнює добутку площі на координату центра її тяжіння
з прямою, що збігається з віссю стержня. Як відомо, статичний момент площі дорівнює добутку площі на координату центра її тяжіння 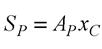 . На цій під ставі маємо
. На цій під ставі маємо
 I нарешті, помітивши, що
I нарешті, помітивши, що  остаточно одержуємо:
остаточно одержуємо: – це окремий випадок відомої з математичного аналізу формули Сімпсона (формули парабол) для обчислення визначених інтегралів, коли інтервал інтегрування розкладається на дві ділянки (рис.3.10):
– це окремий випадок відомої з математичного аналізу формули Сімпсона (формули парабол) для обчислення визначених інтегралів, коли інтервал інтегрування розкладається на дві ділянки (рис.3.10):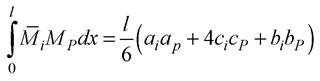
 Процес розв’язання містить чотири етапи:
Процес розв’язання містить чотири етапи:






