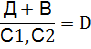Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кількісний етап кінематичного аналізуСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
З погляду кінематичного аналізу кожна споруда складається з дисків і матеріальних точок. Кількісний етап має за мету визначення кількості ступенів вільності всієї розрахункової схеми, тобто сумарної кількості ступнів вільності,які визначають положення елементів системи відносно якоїсь нерухомої системи координат.Цю величину називають ступенем геометричної змінюваності системи.Виходячи з викладених кінематичних властивостей елементів розрахункової споруди,можна записати формулу(Чебишева) для визначення ступня геометричної змінюваності «Г» с-ми: Г=3Д+2В-3П-2Ш-С-3 де Д- кількість простих дисків; В-кількість вузлів в’язей; П-к-ть припайок; Ш-простих шарнірів; С-простих в’язей; 3-число ступнів вільності всієї плоскої розрахункової схеми як твердого тіла в її площині. Ступінь геометричної змінюваності розрахункової схеми,обчислену за формулою,дає змогу визначити її кінематичну характеристику.
Якщо Г›0,розрахункова схема споруди безперечно є геометрично змінюваною. Цей результат засвідчує, що з’єднувальних пристроїв не вистачає для усунення можливості переміщень,які можуть робити окремі елементи системи або вся ця система в цілому. Якщо Г≤0,можна стверджувати,що виконується необхідна умова геометричної незмінюваності розрахункової схеми,бо з’єднувальні пристрої можуть забезпечити нерухомість усих елементів і систем вцілому. Проте з’єднувальні пристрої можуть бути встановлені в такий спосіб,що в однах зонах конструкції кількість їх надмірна,а в інших- недостатня. У деяких випадках особливе розташування з’єднувальних пристроїв може приводити до появи миттєвого центра взаємного обертання елементів системи. Таким чином при Г≤0 розрахункова схема може бути або геом. Незмінюваною, або геом..змінюваною, або нарешті, миттєво змінюваною залежно від розташування дисків і зєднань. Належність до конкретного типу остаточно встановлюється на підставі виконання якісного етапу аналізу розрахункової схеми.
Якісний аналіз. Способи утворення геометрично незмінюваних систем. Можна виділити 5 основних способів з’єднання елементів:

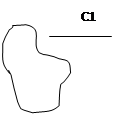
      Спосіб Діади – до диска можна приєднати матеріальну точку(вузол в’язі) за допомогою двох кінематичних в’язей, які не розташовані вздовж однієї прямої. Спосіб Діади – до диска можна приєднати матеріальну точку(вузол в’язі) за допомогою двох кінематичних в’язей, які не розташовані вздовж однієї прямої.
Спосіб Шухова – маємо два будь-яких диска, вони можуть з’єднуватись трьома кінематичними в’язями, які не паралельні між собою і одночасно не перетинаються в одній точці.

 Д1+Д2/С1,С2,С3 =D Д1+Д2/С1,С2,С3 =D
 
    Спосіб Полонсо – два диски можна з’єднати за допомогою шарніра і кінематичної в’язі, які не розташовані на одній прямій. Спосіб Полонсо – два диски можна з’єднати за допомогою шарніра і кінематичної в’язі, які не розташовані на одній прямій.
Д1+Д2/Ш;С=D
Спосіб Припайки – два диска можна з’єднати за допомогою припайки.

 
      Спосіб Шарнірного трикутника – три диски можна попарно з’єднати за допомогою трьох шарнірів, які не лежать вздовж однієї прямої. Спосіб Шарнірного трикутника – три диски можна попарно з’єднати за допомогою трьох шарнірів, які не лежать вздовж однієї прямої.
Д1+Д2+Д3/Ш1;Ш2;Ш3=D
7. Аналіз геометричної структури споруди Якісний (структурний) етап аналізу розрахункової схеми полягає у визначенні послідовності та способів утворення системи з елементів. З'єднання всієї системи або її фрагментів повинно виконуватись відповідно до способів правильного з'єднання елементів у геометрично незмінювані системи. Далі наведеш основні способи утворення найпростіших геометрично незмінюваних плоских систем при використанні мінімальної кількості з'єднувальних пристроїв. Надамо певні назви цим способам для зручності їхнього подальшого викладу. При поданні цих способів і прикладів структурного аналізу зручно використовувати умовну "формулу*, яка розміщується поруч з відповідною схемою з'єднання. Така "формула" виглядає як дріб, де в чисельнику міститься перелік з'єднаних елементів, у знаменнику - перелік з'єднувальних пристроїв, а після знака => - позначення нового укрупненого диска. Якщо з'єднання виконано за допомогою фіктивного шарніра» в знаменнику подається найменування двох в'язей, що утворюють цей шарнір, із символом "х" між ними.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 672; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.134 (0.007 с.) |