
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дійсна і можлива робота зовнішніх зусиль
 Розглянемо статичне завантаження стержня (рис.3.1,а), який внаслідок дії розтягуючої сили P дістає подовження Розглянемо статичне завантаження стержня (рис.3.1,а), який внаслідок дії розтягуючої сили P дістає подовження  Якщо матеріал стержня є фізично-нелінійним, графік залежності між навантаженням і переміщенням кінця стержня буде криволінійним (рис.3.1,б). Для обчислення роботи, яку виконала сила P, візьмемо переміщення u в довільний момент часу і надамо йому приріст du. Тоді робота сили виражається інтегралом Якщо матеріал стержня є фізично-нелінійним, графік залежності між навантаженням і переміщенням кінця стержня буде криволінійним (рис.3.1,б). Для обчислення роботи, яку виконала сила P, візьмемо переміщення u в довільний момент часу і надамо йому приріст du. Тоді робота сили виражається інтегралом
і являє собою площу між кривою і віссю u, яка на графіку (рис.3.1,б) заштрихована вертикальною штриховкою. Таку роботу називають дійсною. Якщо ж надати приріст не переміщенню, а навантаженню, то робота виражатиметься інтегралом
Узагальнені сили і узагальнені переміщення. Універсальні позначення переміщень. З точки зору проблем, що вивчаються будівельною механікою, всі переміщення мають одні й ті самі властивості. Тому зазвичай будь-яке пере-міщення, незалежно від його характеру або від причин, що його зумовлюють, називають узагальненим переміщенням, тобто переміщенням у загальному розумінні цього слова. Кожному переміщенню ставлять у відповідність певну силову дію, яка здійснює роботу на цьому переміщенні. Така силова дія називається узагальненою силою, тобто силовою дією в загальному сенсі слова. Різним узагальненим переміщенням відповідають різні за характером та напрямком узагальнені сили.
Розглянемо кілька прикладів узагальнених переміщень і відповідних цим силам узагальнених сил. 1. Внаслідок деформації споруди точка C переміститься в положення 2. В результаті деформацій споруди точки C і D перемістяться в положення 3. В результаті деформації споруди переріз C стержня повернеться на кут
4. У шарнірі C поєднуються два стержні. В процесі деформації один із стержнів повернеться на кут Будь-яке узагальнене переміщення позначається літерою Продовженя дал
Продовження питання 22 Універсальні позначення переміщень дорівнює одиниці. В позначення вводяться два індекси, наприклад На рис.3.4,а-в зображено три деформованих стани балки, що перебуває під дією різних навантажень.
повороту, від дії сили
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 747; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.41.236 (0.006 с.) |



 Таку роботу називають додатковою. На графіку (рис.3.1,б) площа, що відповідає додатковій роботі, позначена горизонтальною штриховкою. Сума дійсної і додаткової роботи називається повною роботою зовнішніх сил:
Таку роботу називають додатковою. На графіку (рис.3.1,б) площа, що відповідає додатковій роботі, позначена горизонтальною штриховкою. Сума дійсної і додаткової роботи називається повною роботою зовнішніх сил: Очевидно, що повній роботі відповідає площа прямокутника. Для лінійно деформованих систем між навантаженням і переміщенням, що їм зумовлене, існує лінійна залежність (рис.3.1,в). При цьому дійсна робота зображується площею заштрихованого трикутника. Очевидно, що додаткова робота в такому разі дорівнює дійсній роботі:
Очевидно, що повній роботі відповідає площа прямокутника. Для лінійно деформованих систем між навантаженням і переміщенням, що їм зумовлене, існує лінійна залежність (рис.3.1,в). При цьому дійсна робота зображується площею заштрихованого трикутника. Очевидно, що додаткова робота в такому разі дорівнює дійсній роботі: і може бути обчислена як площа трикутника
і може бути обчислена як площа трикутника Означена рівність називається теоремою Клапейрона: в лінійно-деформованих системах дійсна робота статично прикладеної сили дорівнює половині добутку кінцевої величини сили на відповідне кінцеве переміщення, зумовлене цією силою. Отже, робота сили на зумовлених цією силою переміщеннях називається дійсною. Якщо ж сила P, залишаючись незмінною, здійснює роботу на переміщеннях
Означена рівність називається теоремою Клапейрона: в лінійно-деформованих системах дійсна робота статично прикладеної сили дорівнює половині добутку кінцевої величини сили на відповідне кінцеве переміщення, зумовлене цією силою. Отже, робота сили на зумовлених цією силою переміщеннях називається дійсною. Якщо ж сила P, залишаючись незмінною, здійснює роботу на переміщеннях  зумовлених іншими діями, то таку роботу називають можливою. Можлива робота дорівнює добутку величини сили на відповідне переміщення, яке зумовлене іншими силами:
зумовлених іншими діями, то таку роботу називають можливою. Можлива робота дорівнює добутку величини сили на відповідне переміщення, яке зумовлене іншими силами: (рис.3.3,а). зосередженій силі, яка прикладена в точці, відповідає поступальне переміщення цієї точки в напрямі сили.
(рис.3.3,а). зосередженій силі, яка прикладена в точці, відповідає поступальне переміщення цієї точки в напрямі сили.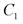 і
і  відповідно (рис.3.3,б). двом однаковим за величиною силам, що спрямовані вздовж однієї прямої назустріч одна одній, відповідає узагальнене переміщення, що характеризує зміну відстані між точками, в яких вони прикладені.
відповідно (рис.3.3,б). двом однаковим за величиною силам, що спрямовані вздовж однієї прямої назустріч одна одній, відповідає узагальнене переміщення, що характеризує зміну відстані між точками, в яких вони прикладені. (рис.3.3,в). При цьому зосереджений момент M, який може бути прикладений в цьому перерізі, здійснить роботу
(рис.3.3,в). При цьому зосереджений момент M, який може бути прикладений в цьому перерізі, здійснить роботу Таким чином, зосередженому моменту відповідає кут повороту перерізу стержня в точці прикладення моменту.
Таким чином, зосередженому моменту відповідає кут повороту перерізу стержня в точці прикладення моменту. , а другий - на кут
, а другий - на кут  рис.3.3,г). двом однаковим за величиною і протилежним за напрямом зосередженим моментам відповідає зміна кута поміж перерізами, в яких ці моменти прикладені.
рис.3.3,г). двом однаковим за величиною і протилежним за напрямом зосередженим моментам відповідає зміна кута поміж перерізами, в яких ці моменти прикладені. , якщо воно зумовлене зовнішньою дією довільної величини, або літерою
, якщо воно зумовлене зовнішньою дією довільної величини, або літерою  якщо величина дії
якщо величина дії Індекси позначають місцезнаходження і характер переміщення, а також дію, що його зумовлює. Перший індекс пов’язаний з характером та напрямом переміщення. Він вказує на узагальнену силу, яка відповідає цим характеристикам. Другий індекс пов’язаний із дією, яка викликає це переміщення.
Індекси позначають місцезнаходження і характер переміщення, а також дію, що його зумовлює. Перший індекс пов’язаний з характером та напрямом переміщення. Він вказує на узагальнену силу, яка відповідає цим характеристикам. Другий індекс пов’язаний із дією, яка викликає це переміщення. Так,
Так,  являє собою переміщення в напрямі сили
являє собою переміщення в напрямі сили  першого стану, тобто прогин балки, від дії сили
першого стану, тобто прогин балки, від дії сили  другого стану;
другого стану;  - переміщення в напрямі сили третього
- переміщення в напрямі сили третього  стану, тобто кут
стану, тобто кут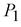 першого стану тощо. І взагалі можна сказати, що
першого стану тощо. І взагалі можна сказати, що  - це переміщення в напрямі узагальненої сили стану i від дії узагальненої сили стану
- це переміщення в напрямі узагальненої сили стану i від дії узагальненої сили стану  Отже, для того щоб позначити будь-яке переміщення, необхідно створити допоміжний стан конструкції, приклавши узагальнену силу, яка відповідає переміщенню. Так, для того, щоб позначити в попередньому прикладі вертикальне переміщення точки k від дії сил стану 1, створимо допоміжний стан k, приклавши в перерізі k балки вертикальну зосереджену силу (рис.3.4,г). Тоді дане переміщення позначатиметься
Отже, для того щоб позначити будь-яке переміщення, необхідно створити допоміжний стан конструкції, приклавши узагальнену силу, яка відповідає переміщенню. Так, для того, щоб позначити в попередньому прикладі вертикальне переміщення точки k від дії сил стану 1, створимо допоміжний стан k, приклавши в перерізі k балки вертикальну зосереджену силу (рис.3.4,г). Тоді дане переміщення позначатиметься 



