
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади обчислення відносних показників.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 1. У звітному році порівняно з базовим випуск продукції на підприємстві зріс на 4,5%, а планом передбачалось підвищити на 5,6%. На скільки відсотків фактично перевиконано чи недоконане планове завдання з випуску продукції? Розв’язок. Згідно з умовою задачі, нам відомо:
Висновок: планове завдання недовиканано на 1%.
Приклад 2. У 2009 році магазином було продано продовольчих товарів на суму 275тис.грн., планом на 2010р. передбачалось продати на 300 тис. грн., фактично було продано на 330 тис. грн.. Визначте відносні показники планового завдання, виконання плану і динаміки. Розв’язок. Згідно з умовою задачі, нам відомо: У0 = 275000 грн.; Упл = 300000 грн., У1 = 330000 грн.
тобто планом на 2010 рік передбачалось збільшити продаж продукції на 9,1%, порівняно з базовим (попереднім) роком.
тобто фактично план продажу товару було перевиконано на 10% у 2010 р.
тобто у 2010 порівняно з 2009р. продаж продукції збільшився на 20%.
Приклад 3. Чисельність народжених у Херсонській області за 2009 рік склала 12323 чол., а середньорічна чисельність населення 1099,2 тис. чол. Визначити коефіцієнт народжуваності. Розв’язок. Маємо приклад в.в. інтенсивності:
Кн=12323*1000:1099200=11,2, , тобто за рік на 1000 осіб населення припадає 11,2 народжених. Іще один приклад. На території в 3000 гектарів росте 9000 хвойних дерев. Знайдіть щільність хвойних лісонасаджень.
Розв’язок. 9000 дерев / 3000 га = 3 дерева на 1 гектар. Приклад 4. На 1 січня 2010 року в Херсонській області проживало505,3 тис. чоловік і 586,7 тис. жінок. Отже, на кожних 100 чоловік припадає 586,7: 505,3 * 100 = 116 жінок, або на кожні 100 жінок припадає 505,3: 586,7 * 100 = 86,1 чоловіків. А на кожні 1000 жінок припадає 861 чоловік. В даному разі маємо приклад в.в. координації.
Прилад 5. Охарактеризувати інтенсивність зміни виробництва електроенергії атомними електростанціями за такими даними:
Розв’язок. За наведеними даними обчислимо відносні величини динаміки зі змінною (розрахунок 1) і сталою (розрахунок 2) базами порівняння.
Розрахунок 1:
Розрахунок 2:
Приклад 6. Станом на 1 січня 2010р. чисельність населення Херсона становила 338062 особи, а Каховки –37295 осіб. Розрахуємо відносну величину порівняння у просторі, взявши за базу порівняння чисельність населення міста Каховки: 338062: 37295 = 9,1. Отже, чисельність населення міста Херсона в 9,1 раза більша від чисельності населення міста Каховки. Приклад 7. У групі 25 студентів. Серед них 8 осіб чоловічої статі,17-жіночої. Питома вага осіб чоловічої статі становитиме (8:25)*100 %=32%, а жіночої (17:25)*100%= =68%. Разом: 32%+68%=100%. В даному разі розраховано відносну величину структури.
№1. Відомі такі дані про виробництво валової продукції на с/г підприємстві (млн..грн.):
Визначте відносну величину планового завдання (%).
№2. Фактичний обсяг валової продукції с/г підприємства склав за рік 210 млрд. грн.. Планове завдання з валової продукції виконано на 107,0%. Визначте план валової продукції (млрд..грн.).
№3. Планове завдання виробництва продукції у звітному періоді перевиконано на 6%. Фактичний обсяг у порівнянні з базисним періодом зріс на 10%. Визначте відносну величину планового завдання.
№4. Відомі такі дані про споживання населенням Херсонської області картоплі (на 1 особу за рік, кг):
Визначте відносну величину динаміки базисним способом.
№5. Плановий обсяг виробництва продукції заводу становив 550 млн. грн.. Планове завдання перевиконано на 6,1 %. Визначити фактичний обсяг продукції заводу в абсолютному вираженні.
№6. Планом передбачено зростання товарообігу магазина на 7,1 %. Фактичний товарообіг у звітному періоді у порівнянні з базисним зріс на 8,3%. Визначте процент виконання плану товарообігу у звітному періоді.
№7. Сільгосппідприємство у 2009 р. виробило 2500 ц яловичини. Планом на 2010 рік передбачено збільшити виробництво яловичини на 27 %. Фактично вироблено у 2010 році 3200 ц яловичини. Визначте процент виконання плану у 2010 р.
№8. Планом на звітний період передбачено збільшити продуктивність праці на 6,1%. Фактичне збільшення продуктивності праці склало 8,3%. Визначте процент виконання плану зростання продуктивності праці.
№9. Виконання річного замовлення закупок кавунів та динь підприємствами харчової промисловості характеризується такими даними:
Визначте фактичну кількість закупленої продукції.
№10. Виконання плану виробництва продукції с/г підприємством склало за 2009 рік 100,1 % при плані 2009р. – 18550 млн.грн. Визначте фактичну суму виконання плану виробництва сільськогосподарської продукції за рік.
№11. Середньомісячна заробітна плата працівників у Херсоні та Києві в 2009р. характеризувалась такими даними (грн.):
Визначте відносну величину порівняння.
№12. Кількість населення Херсонської області на початок 2010 р. складало 1093,4 тис. осіб, а територія – 28,5 тис. кв. км. Визначте відносну величину інтенсивності.
№13. Бригада орендарів обслуговує 420 корів. За рік вироблено 15436 ц молока. Витрати кормів подані у таблиці. Визначте: 1) загальний обсяг і структуру витрачених кормів; 2) витрати кормів (у кормових одиницях) на 1 голову і на 1 ц молока; 3) продуктивність корів; 4) зазначте вид відносних величин у кожному випадку.
№14. На 1 листопада загальна земельна площа та розподіл сільськогосподарських угідь регіону становили, млн..га: загальна площа 2,0 у т.ч. с/г угіддя 1,5 з них: рілля 1,2 сіножаті та пасовища 0,3 Визначте відносні величини, які б характеризували: а) частку с/г угідь та ріллі у загальній земельній площі; б) частку ріллі у площі с/г угідь; в) співвідношення площі ріллі з площею сіножаті та пасовищ. Зробіть висновки.
№15. За наведеними даними визначте окремо для чоловіків та жінок відносні величини, які б характеризували: а) частку безробітних, які отримують допомогу з безробіття; б) частку безробітних, які проходять професійне перенавчання. Проведіть порівняльний аналіз розрахованих часток. Окрім того, визначте частку жінок серед безробітних, що отримують допомогу, та серед безробітних, які проходять професійне перенавчання. Зробіть висновки.
№16. На основі даних про розподіл населення регіону за віком та типом населення визначте відносні величини, які б характеризували: а) структуру міського і сільського населення за ознакою працездатності, проведіть порівняльний аналіз структур; б) співвідношення працездатного і непрацездатного населення у містах і селах; в) структуру населення за типом поселень; г) співвідношення міського і сільського населення. Зробіть висновки.
№17. Класифікуйте наведені статистичні показники та визначте вид відносних величин: 1) виробництво електроенергії на душу населення за рік, кВт/год; 2) довжина електрифікованих ліній залізниць на кінець року, км; 3) кількість лікарів на 10000 населення на початок року; 4) введення в дію загальної площі житлових будинків за рік, тис.кв.м; 5) співвідношення роздрібного товарообігу продовольчих та промислових товарів; 6) частка інвестицій на охорону навколишнього середовища у загальному обсязі капіталовкладень; 7) зростання витрат на заходи з охорони праці у поточному році порівняно з минулим, %; 8) кількість зареєстрованих за рік шлюбів на 1000 чол. населення; 9) розмір основних виробничих фондів на 100 га с.- г. угідь на початок року, тис. гр. од.; 10) кількість голів ВРХ відповідної групи (за статтю або за віком) припадає на 100 корів. № 18. На певний момент часу чисельність міського населення України становила 34,8 млн. чоловік, а сільського – 16,5 млн. чоловік. Обчисліть відносну величину координації. Зробіть висновки. № 19. Є такі дані про ВВП і доходи зведеного і державного бюджету України за певний період часу:
Обчисліть всі можливі види відносних величин і вкажіть, до якого виду вони належать.
№ 20. Для двох ТОВ є дані про площу земельних угідь, поголів’я тварин, вихід продукції тваринництва, вартість основних фондів:
Обчислить відносні показники інтенсивності, які характеризують для ТОВ: а) виробництво валової продукції тваринництва на 100 га; б) виробництво м’яса ВРХ на 100 га с.- г. угідь; в) поголів’я корів на 100 га.
Контрольні запитання і завдання 1. Що таке абсолютні статистичні величини і яке їхнє значення в статистиці? 2. Які види абсолютних величин можна виділити за способом їх вираження? 3. В яких одиницях можна виражати абсолютні величини? 4. Що називають відносною величиною? 5. В якій формі можна виражати відносні величини? 6. Які види відносних величин Ви знаєте? 7. Як обчислюють відносні величини планового завдання? 8. Що характеризують відносні величини динаміки і яка послідовність їх обчислення? 9. Що виражають відносні величини структури та координації? 10. Для характеристики яких явищ використовують відносні величини інтенсивності і порівняння в просторі?
СЕРЕДНІ ВЕЛиЧИНИ Методичні вказівки Середня – в статистиці – абстрактна, узагальнююча величина, що характеризує рівень варіюючої ознаки в якісно однорідній сукупності. Коливання індивідуальних значень ознаки, викликані дією різних факторів, урівноважуються в середній величині, погашаються при усередненні і в середній виявляються загальні властивості, характерні для певного масового явища. Основною умовою наукового застосування середніх величин є якісна однорідність сукупності, для якої обліковується середня. Отже, обчислення і використання середніх величин тісно пов’язані з методом статистичних групувань, за допомогою яких різнорідні явища розподіляються на якісно однорідні сукупності. Середні величини для неоднорідних сукупностей не мають наукового і пізнавального значення. Середні величини можуть бути абсолютними або відносними. Їх виражають в тих самих одиницях вимірювання, що й усереднені ознаки. Основні завдання розрахунку середніх величин – це характеристика зміни явищ у динаміці, тенденції у розвитку явищ, співвідношення двох або кількох рівнів, зв’язків і залежностей між явищами, виявлення нового, прогресивного та найбільш поширеного розвитку явища. В статистиці застосовують різні види середніх величин: середню арифметичну, середню гармонічну, середню геометричну, та ін. Вибір конкретного виду середньої величини залежить від характеру вихідних даних. Критерій правильного вибору форми середньої величини – це запис логічної форми розрахунку. Кожна із зазначених середніх може набувати дві форми – просту і зважену. Середня арифметична є найбільш поширеним видом середніх величин. Її застосовують тоді, коли загальний обсяг варіюючої ознаки для усієї сукупності становить суму індивідуальних значень усередненої ознаки. Наприклад, загальний збір урожаю цукрових буряків є сумою урожаїв цієї культури з кожного гектара площі, загальний надій молока є сумою надоїв молока від кожної корови і т.д. Розрізняють середню арифметичну просту і зважену: · Проста хі – варіанти, тобто значення ознаки і -ї одиниці сукупності; n – число варіант, тобто обсяг сукупності. Використовується за первинними, незгрупованими даними, коли відомі чисельник і знаменник дробу. · Зважена хі – варіанта; fі – частота (вага) або питома вага (частость). Використовується за згрупованими даними, коли знаменник дробу логічної формули середньої відомо, а чисельник – ні.
Середню гармонічну використовують для узагальненої характеристики ознаки тоді, коли відомі окремі значення досліджуваної ознаки і обсяги явищ, а частоти не відомі. Вона буває простою і зваженою. · Проста: n – число варіант, тобто обсяг сукупності хі – варіанта; Використовується за незгрупованими даними, коли чисельник дробу логічної формули відомо, а знаменник – ні.
· Зважена: Wi = xifi – обсяг значень ознаки. Використовується за згрупованими даними, коли чисельник дробу логічної формули відомий, а знаменник – ні.
Середню геометричну використовують для обчислення середніх темпів зростання, тобто коли загальний обсяг явищ становить не суму, а добуток ознак. · Проста: П – символ добутку; хі – ланцюгові темпи зростання в рядах динаміки.
Середня квадратична використовується при визначенні показників варіації. Проста:
Поряд з цими середніми величинами в статистиці використовують також структурні середні – моду і медіану.
Мода (Мо) – значення варіанти (конкретне значення ознаки, що варіює), яке найчастіше повторюється в ряді розподілу. У дискретному ряді моду легко відшукати візуально, в інтервальному ряді легко відшукати модальний інтервал, а приблизне значення моди обчислюється за формулою:
xMo – нижня межа модального інтервалу; hMo – розмір модального інтервалу; fMo – частота модального інтервалу; fMo-1 – частота попереднього інтервалу; fMo+1 – частота інтервалу, наступного за модальним. Звичайно зустрічаються ряди з одним модальним значенням ознаки. Якщо у ряді два або більше модальних значень, він називається відповідно бімодальним та мультимодальним. Медіана (Ме) – варіанта, що ділить ранжирований ряд на дві рівні за чисельністю частини. Так, якщо в ряді розподілу робітників за віком Ме =34, то це означає, що половина з них менші цього віку, половина старші цього віку. Коли ряд містить парне число членів, медіана дорівнює середній із двох значень розташованих в середині ряду. Для знаходження медіани в дискретному ряді спочатку обчислюють півсуму частот, а потім визначають, яка варіанта припадає на неї. Для інтервального ряду медіану обчислюють за формулою:
xMe – нижня межа медіанного інтервалу; hMe – розмір медіанного інтервалу; (∑f)/2 – півсума частот медіанного інтервалу; SMе-1 – сума накопичених частот перед медіанним інтервалом; fMе – частота медіанного інтервалу.
Примітка: медіанний інтервал визначається за графою SMе - накопичена частота.
Приклад 1. Статутний фонд акціонерної компанії, сформований 6 засновниками; розмір внеску кожного із них становить, млн..грн.: 6;10;12;9;7;4. Середній внесок одного засновника обчислюється за формулою середньої арифметичної простої:
Приклад 2. Квартальний оборот універсальних бірж протягом року становив, млн..грн.: Ікв. – 372; ІІкв. – 423; ІІІкв. – 340; IVкв. – 455. Середньоквартальний оборот бірж становить: Приклад 3. Середній виробіток продукції одним робітником за зміну в двох цехах підприємства, які виробляють однорідну продукцію, характеризуються такими даними:
Визначити середньоденну продуктивність праці робітників: а) по першому цеху; б) по другому цеху. Зробити висновки. Розв’язок:
1. Обчислення середньої величини починається із запису логічної формули розрахунку:
2. Дивимось, що нам відомо згідно з умовою задачі, і обираємо формулу середньої величини. а) По цеху №1 не відомі дані чисельника смислової формули, а знаменника відомі, використовується формула середньої арифметичної зваженої:
б) По цеху №2 відомі дані чисельника логічної формули розрахунку і не відомі дані знаменника, тому використовується формула середньої гармонічної зваженої:
Висновок: У середньому за зміну по цеху 1 один робітник виготовляє продукції обсягом 33 шт., а по цеху 2 – 30 шт. Таким чином, продуктивність праці робітників цеху1 вища, ніж цеху 2 у середньому на 3 шт. (35 - 30), або на (33/30*100-100)=10%.
Приклад 4. За наведеними даними про продаж картоплі визначити середній процент виконання плану.
xi – значення варіант Wi – обсяг явища (Wi = fi * xi)
Середній процент виконання плану
Приклад 5. Є такі дані про товарні запаси на складі (тис.грн.) та їх рух: на 01.01.2010 було запасів на 200 тис.грн; на 01.04.2010 надійшло товарів на 20тис.грн., на 01.07.2010 відвантажено товару на 14 тис.грн.; на 01.10.2010 надійшло на 10 тис.грн. До кінця року руху не спостерігалось. Визначити середні залишки товарних запасів на складі за 2010 рік. Розв’язок: Побудуємо моментний ряд з рівними інтервалами (3 міс.) згідно з умовою задачі:
01.01.2010 – 200 тис.грн.; 01.04.2010 – 220 тис.грн.; 01.07.2010 – 206 тис.грн.; 01.10.2010 – 216 тис.грн.; 01.01.2010 – 216 тис.грн..
Треба використовувати формулу середньої хронологічної:
Висновок: В середньому щомісячно протягом 2010 року залишки товарних запасів на складі становили 212500 грн.
Приклад 6. (Методика обчислення медіани). Є такі дані про розподіл робітників підприємства за віком:
Визначити медіану і зробити висновки. Розв’язок: Медіанним є інтервал 20-25 років, тому що на нього припадає перша накопичена частота, яка перевищує половину всього обсягу сукупності (57 перевищує
xMe = 20; hMe = 5; ∑ni = 100; SMe-1 = 13; nMe= 44.
Висновок: на підприємстві половина робітників молодша 24,2 року, а половина старша.
Приклад 7. (Методика обчислення моди). Є такі дані про розподіл робітників за рівнем заробітної плати.
Визначити моду і зробити висновок. Розв’язок: Інтервал, в якому міститься мода, становить 150 – 200 грн., тому що цей інтервал має найбільшу частоту:
xMо = 150; hMо = 50; nMо= 32; nMо-1=13; nMо+1=25.
Висновок: на підприємстві найчастіше зустрічаються робітники із заробітною платою = 186 грн.50 коп.
№1. Відомо, що тарифний розряд робітників бригади, яка складається з восьми чоловік, становить: 3,4,3,5,4,5,4,4. Знайти середній рівень кваліфікації робітників бригади.
№ 2. Відомі такі дані:
Визначте середню місячну заробітну плату робітників.
№ 3. На підставі даних визначити середній розмір посівної площі і середньої урожайності картоплі для групи господарств:
№4. Маємо дані про врожайність і валовий збір ячменю за звітний рік. Обчислити середню врожайність ячменю у цілому.
№5. По молочнотоварній фермі є дані про добовий надій молока від 200 корів. Потрібно визначити середній надій молока від корови.
№6. Відомі такі дані по трьох магазинах:
Визначте середню зарплату у трьох магазинах. №7. Маємо дані про заробітну плату та кількість співробітників кафедри у розрізі (професори, лаборанти) за два періоди.
Розрахуйте середню заробітну плату за вересень і жовтень.
№ 8. Є такі дані про чисельність населення міста. На 01.01.2010 – 100 тис.осіб; На 01.04.2010 - 103тис.осіб; На 01.07.2010 – 106 тис.осіб; На 01.10.2010 – 104 тис.осіб; На 01.01.2011 – 110 тис.осіб. Визначити середньорічну чисельність населення міста.
№ 9. Маємо дані про чисельність с/г виробниів на початок місяця: 1.01 – 400, 1.02 – 420, 1.03 – 405, 1.04 – 436, 1.05 – 450, 1.06 – 472, 1.07 – 496, 1.08 – 450, 1.09 – 412, 1.10 – 318, 1.11 – 231, 1.12 – 235, 1.01 – 300. Визначити: а) середньмісячну кількість с/г робітників у І та ІІ півріччях; б) середньорічну кількість;в) змінення чисельності у ІІ півріччі в порівнянні з І.
№ 10. Відомі такі дані про ціну цибулі та кількість продавців на ринку:
Визначте модальну ціну цибулі.
№ 11. Є дані про середній надій молока від корови за рік і про валове виробництво молока. Обчислити середній надій молока від корови.
№ 12. Маємо дані про стаж роботи трактористів в одному господарстві області:
Визначити середній стаж роботи трактористів. № 13. Виконання плану виробництва продукції характеризується даними на п’яти підприємствах галузі. Визначити середній відсоток виконання плану в цілому на підприємствах. Зробити висновки.
№ 14. Є дані про виробництво та питому вагу бракованих виробів. Знайдіть середній процент браку.
№ 15. Є дані про обсяги реалізації на двох виробничих об’єднаннях галузі:
Визначте середній відсоток виконання плану реалізації продукції по об’єднаннях № 1 і № 2.
Контрольні запитання і завдання 1. Що таке середня величина? 2. Яке місце належить середнім величинам серед статистичних методів? 3. Які розрізняють види середніх величин? 4. Які умови застосування середніх величин? 5. Коли використовують середню арифметичну? 6. Які розрізняють види середньої арифметичної? 7. Які умови використання середньої гармонійної? 8. Які розрізняють види середньої гармонійної? 9. Назвіть інші види середніх величин. 10. Що таке мода і медіана? 11. Як визначають моду в дискретному та інтервальному рядах? 12. Назвіть особливості визначення медіани в дискретному та інтервальному рядах.
ПОКАЗНИКИ ВАРІАЦІЇ Методичні вказівки Варіація ознаки є властивістю статистичної сукупності. Варіація – коливання значення ознаки в окремих одиниць сукупності. Для вимірювання варіації в статистиці використовуються різні показники: розмах варіації, середнє лінійне відхилення, середнє квадратичне відхилення, дисперсія і коефіцієнт варіації. Розмах варіації – це різниця між найбільшим і найменшим значеннями ознаки: R = xmax – xmin. Розмах варіації відображає лише крайні значення ознаки і дає тільки приблизну оцінку варіації. Так, для всіх жителів міста розмах варіації може бути більшим за 100 років, для студентів вузу – значно меншим. Середнє лінійне відхилення – це арифметична середня з абсолютних значень відхилень окремих варіантів від їх середньої арифметичної: а) для арифметичної простої
б) для арифметичної зваженої
Примітка: недоліком цього показника є те, що ці відхилення при підсумуванні або множенні беруться без врахування їх знаків. Середнє квадратичне відхилення – це корінь квадратний з середнього квадрата відхилень окремих варіантів від їх середньої арифметичної: а) для арифметичної простої
б) для арифметичної зваженої
Чим менше Примітка: Квадрат величини Дисперсія – це середня з квадратів відхилень окремих варіантів від їх середньої арифметичної: а) для арифметичної простої
б) для арифметичної зваженої
Дисперсія – безрозмірна величина. Дисперсія і середнє квадратичне відхилення призначені вимірювати варіацію ознаки. Відносною мірою коливання є коефіцієнт варіації. Коефіцієнт варіації – це процентне відношення середнього квадратичного відхилення до середньої арифметичної:
Примітка: коефіцієнт варіації дозволяє зіставити варіацію різних ознак, а також зрівняти варіацію однієї ознаки в кількох сукупностях. Розрізняють такі значення варіації: незначну Критерієм однорідності сукупності вважається коефіцієнт варіації
№1. Визначити середнє квадратичне відхилення, якщо відомо, що середня величина ознаки – 260, а коефіцієнт варіації складає 30%.
№2. Середня величина ознаки дорівнює 20, а коефіцієнт варіації 25%. Визначити дисперсію.
№3. Дисперсія ознаки складає 360000, коефіцієнт варіації -50%. Визначити середню величину оз
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 6318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

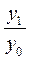 =104,5 або 1,045,
=104,5 або 1,045,  =105,6, або 1,056.
=105,6, або 1,056. , або 99%.
, або 99%.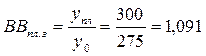 , або 109,1 %,
, або 109,1 %, , або 110%,
, або 110%, , або 120%,
, або 120%, ;
;  ;
;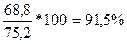 ;
;  .
. ;
;  ;
; ;
;  ;
;  .
. Задачі для самостійного розв’язування
Задачі для самостійного розв’язування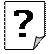

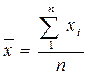 , де
, де , де
, де , де
, де , де
, де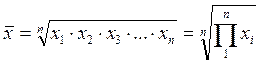 , де
, де Зважена:
Зважена: 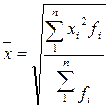
 , де
, де
 , де
, де Приклади обчислення середньої величини.
Приклади обчислення середньої величини. =8 млн.грн.
=8 млн.грн.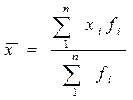 =
=  шт.
шт. =
=  шт.
шт. – середнє значення ознаки.
– середнє значення ознаки. .
.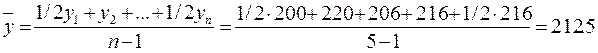 тис.грн.
тис.грн. пі:2 = 100: 2 = 50). Визначимо медіанне значення віку робітників підприємства:
пі:2 = 100: 2 = 50). Визначимо медіанне значення віку робітників підприємства: , де
, де року.
року. , де
, де грн..
грн.. Задачі для самостійного розв’язування
Задачі для самостійного розв’язування


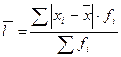 .
.
 .
. , тим повніше середня відображає всю сукупність.
, тим повніше середня відображає всю сукупність.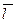 та
та  є іменованими величинами, вони виражаються в тих одиницях вимірювання, що й індивідуальні ознаки.
є іменованими величинами, вони виражаються в тих одиницях вимірювання, що й індивідуальні ознаки.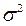 називається дисперсією.
називається дисперсією.

 .
. %; середню
%; середню  10,1 – 30; велику
10,1 – 30; велику  >30%.
>30%.


