
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад 2.3 Оператори додавання і відніманняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 2.4 Оператори ділення і множення
Приклад 2.5 Оператори факторіала і модуля
Приклад 2.6. Оператори знаходження кореня і введення в ступінь
Приклад 2.7. Оператор зміни пріоритету
Д Диференціювання, похідні вищих порядків: застосування, пояснення, приклади. Диференціювання За допомогою Mathcad можна обчислювати похідні скалярних функцій будь-якої кількості аргументів, від 0-го до 5-го порядку включно. І функції, і аргументи можуть бути як дійсними, так і комплексними числами. Для того, щоб продиференціювати функцію f(х) у деякій точці: 1. Визначте точку х, у якій буде обчислена похідна, наприклад, х:=1.2; 2. Введіть оператор диференціювання натискуванням кнопки Derivative (Похідна) на панелі Calculus (Обчислення) чи введіть з клавіатури знак питання <?>. 3. У покажчиках, що з'явилися (мал. 6.3) введіть функцію, що залежить від аргументу х, тобто f(х), і ім'я самого аргументу х. 4.. Введіть оператор <=> чисельного чи <
Чисельне та символьне диференціювання функції f(x)=cos(x)*ln(x) наведено в прикладі 6.5. Потрібно не забути попередньо визначати точку, у якій відбувається чисельне диференціювання, як це зроблено в першому рядку прикладу 6.5.
Приклад 6.5. Чисельне і символьне диференціювання В якості функції диференціювання може використовуватись функція користувача (приклад 6.6)
Приклад 6.6 Символьне і чисельне диференціювання функції користувача
Похідні вищих порядків Mathcad дозволяє чисельно визначати похідні вищих порядків, від 0-го до 5-го включно. Щоб обчислити похідну функції f (х) N-го порядку в точці х, потрібно проробити ті ж самі дії, що і при взятті першої похідної, за тим виключенням, що замість оператора похідної необхідно застосувати оператор похідної N-го порядку (Nth Derivative). Цей оператор вводиться з тієї ж панелі Calculus (Обчислення), або з клавіатури натискуванням клавіш <Ctii>+<Shift>+</>, і містить ще два покажчика, у які варто помістити число N. Чисельне та символьне обчислення похідної другого порядку наведено в прикладі 6.7.
Приклад 6.7 Чисельне і символьне обчислення другої похідної
Дійсні та комплексні числа: призначення, застосування і приклади.
Дійсні числа Будь-який вираз, що починається з цифри, Mathcad інтерпретує як число. Тому для введення числа потрібно його просто набрати на клавіатурі. Mathcad зберігає всі числа в однаковому форматі, але вводити їх можна в найбільш зручному вигляді (notation), виходячи з контексту документа: - як ціле число; - як десяткове число (decimal notation) з будь-якою кількістю десяткових цифр після крапки; - у представленні з порядком (exponential notation). В цьому випадку після введення числа потрібно надрукувати символ множення і ввести 10 у потрібному ступені; - як число в іншій системі числення (. двійковій (binary), восьмиричній (octal) або шістнадцятирічній (hexadecimal).
Приклад 3.1. Введення дійсних чисел Комплексні числа Більшість операцій у середовищі Mathcad за замовчуванням здійснюється над комплексними числами. Комплексне число є сумою дійсного й уявного числа, щовиходить шляхом множення будь-якого дійсного числа на уявну одиницю (imaginary unit) i. За визначенням, i =
Мал.3.1 Введення уявної одиниці
Приклад 3.2. Комплексні числа Для роботи з комплексними числами є кілька простих функцій і операторів (Див. приклад 3.3). Базові з них: Re(z) - дійсна частина комплексного числа z; im(z) - уявна частина комплексного числа z; arg(z) - аргумент комплексного числа z;
Приклад 3.3. Базові функції роботи з комплексними числами
З
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.178 (0.011 с.) |



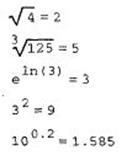
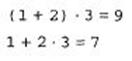
 > символьного виводу для отримання відповіді.
> символьного виводу для отримання відповіді.




 або
або  . Комплексне число можна ввести у вигляді звичайної суми дійсної і уявної частин, чи у вигляді будь-якого виразу, що містить уявне число. Уявну одиницю можна позначити символом і або j. Щоб ввести уявну одиницю потрібно натиснути клавіші <1>та <i>. Якщо просто ввести символ "i", то Mathcad інтерпретує його як змінну i. Крім того, уявна одиниця має вигляд 1i тільки тоді, якщо відповідна формула виокремлена. В протилежному випадку уявна одиниця відображається просто як символ i (Мал.3.1). Введення і виведення комплексних чисел ілюструється прикладом 3.2.
. Комплексне число можна ввести у вигляді звичайної суми дійсної і уявної частин, чи у вигляді будь-якого виразу, що містить уявне число. Уявну одиницю можна позначити символом і або j. Щоб ввести уявну одиницю потрібно натиснути клавіші <1>та <i>. Якщо просто ввести символ "i", то Mathcad інтерпретує його як змінну i. Крім того, уявна одиниця має вигляд 1i тільки тоді, якщо відповідна формула виокремлена. В протилежному випадку уявна одиниця відображається просто як символ i (Мал.3.1). Введення і виведення комплексних чисел ілюструється прикладом 3.2.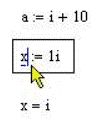

 - модуль комплексного числа z;
- модуль комплексного числа z;



