
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення криволінійних інтегралів першого та другогоСодержание книги
Поиск на нашем сайте
Роду. Формула Гріна. Умови незалежності криволінійного Інтеграла від шляху інтегрування
Нехай Криволінійним інтегралом першого роду від функції
Нехай на кусково-гладкій просторовій кривій
де К риволінійним інтегралом другого роду від векторної функції
де Для криволінійних інтегралів першого і другого роду має місце залежність:
де
Властивості криволінійних інтегралів
1. Криволінійні інтеграли першого й другого родів не залежать від вибору початкової точки на цьому контурі. 2. Криволінійний інтеграл першого роду не залежить від напряму обходу шляху інтегрування.
3. Інтеграл другого роду залежить від напряму обходу дуги
4. Теорема про середнє. Якщо функція гладкій дузі точка
де Тобто криволінійний інтеграл першого роду дорівнює добутку середнього значення підінтегральної функції на довжину шляху інтегрування.
Обчислення криволінійних інтегралів першого роду За плоскою областю I. Крива координатами
II. Крива
III. Крива
Обчислення криволінійних інтегралів другого роду За плоскою областю I. Крива тами
II. Крива
III. Крива
Формула Гріна встановлює зв’язок між подвійним інтегралом по плоскій області й криволінійним інтегралом по контуру цієї області. Формула Гріна має вигляд:
де Г – контур області Нехай функції
не залежить від шляху інтегрування, а лише від початкової й кінцевої точок інтегрування та від функцій
Зразки розв’язування задач
Приклад 1. Обчислити криволінійний інтеграл
Розв’язання. Рівняння прямої, якій задовольняють задані точки, знаходиться за формулою:
де Пряма За формулою (4.1) матимемо
Приклад 2. Обчислити криволінійний інтеграл першого роду Розв’язання. Перейдемо до полярних координат:
Приклад 3. Обчислити криволінійний інтеграл першого роду
Розв’язання. Знайдемо похідні функцій
За формулою (4.5) матимемо
Приклад 4. Обчислити криволінійний інтеграл Розв’язання. Запишемо рівняння прямої, що проходить через точки
Тоді
Приклад 5. Обчислити інтеграл
Розв’язання. Вздовж ламаної Тому, згідно з формулою (4.4), маємо:
Приклад 6. Обчислити інтеграл Розв’язання. Розглянемо полярну систему координат:
За формулою (4.3) маємо
Приклад 7. За допомогою формули Гріна обчислити криволінійний інтеграл Розв’язання. За умовами задачі
За формулою Гріна
Область
Перейдемо до полярних координат з полюсом у центрі Таким чином,
Приклад 8. Чи залежить криволінійний інтеграл від шляху інтегрування Розв’язання. За умовами задачі: Отже, інтеграл залежить від шляху інтегрування.
Завдання для самостійної роботи
I. Обчислити криволінійні інтеграли: а) б) в) г) д)
е)
II. За допомогою формули Гріна обчислити криволінійний інтеграл
III. Вказати криволінійний інтеграл по координатах, який не залежить від шляху інтегрування а) б) в)
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 2415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.008 с.) |

 кусково-гладка просторова крива з початком у точці
кусково-гладка просторова крива з початком у точці  і кінцем в точці
і кінцем в точці  , на якій визначена і неперервна функція
, на якій визначена і неперервна функція  . Інтегральною сумою розбиття дуги
. Інтегральною сумою розбиття дуги  на
на  елементарних частин довжини
елементарних частин довжини  називається наступна функція
називається наступна функція  , де
, де  довільна точка на елементарному відрізку
довільна точка на елементарному відрізку 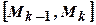 розбиття.
розбиття. при
при  та
та  , яка не залежить від способу розбиття дуги
, яка не залежить від способу розбиття дуги  на елементи і вибору точок
на елементи і вибору точок  в частинних дугах довжини
в частинних дугах довжини  і позначається таким чином:
і позначається таким чином: .
.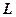 задана векторна функція
задана векторна функція  , яка має проекції
, яка має проекції  на осі вибраної декартової системи координат. Інтегральною сумою розбиття дуги
на осі вибраної декартової системи координат. Інтегральною сумою розбиття дуги  з проекціями
з проекціями  називається функція:
називається функція:
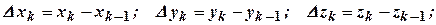
 довільна точка на
довільна точка на  .
. по дузі
по дузі  при
при  (якщо вона існує і не залежить від способу розбиття дуги
(якщо вона існує і не залежить від способу розбиття дуги  ,
, радіус вектор точки;
радіус вектор точки;  скалярний добуток.
скалярний добуток. ,
, проекція вектора
проекція вектора 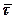 , який напрямлений по дотичній до дуги
, який напрямлений по дотичній до дуги 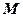 в бік від
в бік від  .
. , для якої має місце наступна рівність:
, для якої має місце наступна рівність: .
. довжина дуги
довжина дуги  задається рівнянням
задається рівнянням  , а точки
, а точки  :
: . (4.1)
. (4.1) де
де  .
. . (4.2)
. (4.2) , де
, де  .
. . (4.3)
. (4.3) :
: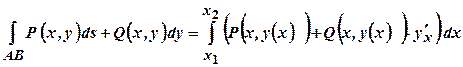 . (4.4)
. (4.4) .
. . (4.5)
. (4.5)
 . (4.6)
. (4.6) ,
, функції неперервні в області
функції неперервні в області  , для яких існують неперервні частинні похідні
, для яких існують неперервні частинні похідні  і
і  .
. визначені і неперервні в однозв’язній обмеженій замкненій області
визначені і неперервні в однозв’язній обмеженій замкненій області  . Тоді величина криволінійного інтеграла
. Тоді величина криволінійного інтеграла
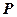 і
і 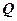 , якщо буде виконуватися рівність:
, якщо буде виконуватися рівність:
 , де
, де  і
і  .
. ,
,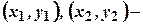 задані точки.
задані точки. має вигляд:
має вигляд:  або
або  . Звідси
. Звідси  .
.
 .
. , де
, де  .
.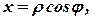
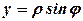 . Рівняння кривої
. Рівняння кривої  , де
, де  . Для обчислення інтеграла застосуємо формулу (4.3), оскільки
. Для обчислення інтеграла застосуємо формулу (4.3), оскільки  . Отже
. Отже ;
;

 .
. , де
, де  між точками
між точками  та
та  .
.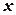 та
та 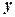 за параметром
за параметром  :
: .
.
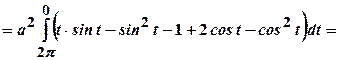
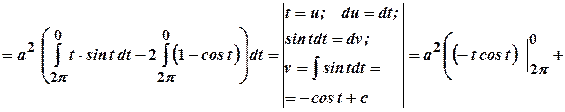
 .
. , де
, де  до точки
до точки  .
. .
. . Скористаємось формулою (4.4):
. Скористаємось формулою (4.4):
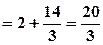 .
. вздовж ламаної
вздовж ламаної  , де
, де  і
і  .
. маємо
маємо 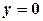 і
і  , на ділянці
, на ділянці 
 .
.
 .
. , де
, де  від
від  до
до  .
. ,
,  .
.
 .
. , де
, де  .
. ;
; . Отже
. Отже  .
.
 .
. коло з центром в точці
коло з центром в точці  і радіусом
і радіусом 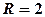 . Рівняння кола має вигляд:
. Рівняння кола має вигляд: .
. . Рівняння, яке зв’язує
. Рівняння, яке зв’язує  і полярні координати
і полярні координати  з полюсом у точці
з полюсом у точці 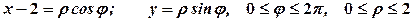 .
.

 .
. ?
? . Знайдемо часткові похідні
. Знайдемо часткові похідні  .
. де
де  і
і  ;
; , де
, де 
 ;
; , де
, де  ;
; де
де 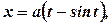

 ;
; , де
, де  по ходу стрілки годинника;
по ходу стрілки годинника; , де
, де  від точки
від точки  до точки
до точки 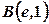 .
. , де
, де  .
. ;
; ;
; .
.


