
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод варіації довільних сталих.Содержание книги
Поиск на нашем сайте
Розглянемо лінійне неоднорідне диференціальне рівняння другого порядку з постійними коефіцієнтами:
де Розв’язок цього рівняння буде мати вигляд:
де
Приклад 1. Розв’язати рівняння:
Розв’язання. Знайдемо розв’язок відповідного однорідного рівняння:
Загальний розв’язок початкового рівняння буде мати той же вигляд, що і загальний розв’язок однорідного рівняння, але
Розв’яжемо цю систему за формулами Крамера:
Тоді Дістанемо функції
Отже, загальний розв’язок рівняння отримаємо у вигляді:
Приклад 2. Розв’язати рівняння:
Розв’язання. Частинні розв’язки відповідного однорідного рівняння Загальний розв’язок лінійного неоднорідного рівняння отримаємо у вигляді
Цю систему розв’яжемо за формулами Крамера
Отже, Проінтегруємо останні два рівняння:
Маємо під знаком інтеграла правильний раціональний дріб, який розкладемо на простіші:
Звідки, дістанемо:
Отже, Обчислимо окремо
Загальний розв’язок лінійного неоднорідного рівняння дістанемо у вигляді
Приклад 3. Розв’язати рівняння:
Розв’язання. Характеристичне рівняння Загальний розв’язок неоднорідного рівняння шукатимемо у вигляді
Проінтегруємо кожне з отриманих рівнянь:
Дістанемо загальний розв’язок початкового рівняння:
Приклад 4. Розв’язати задачу Коші:
Розв’язання. Частинні розв’язки відповідного однорідного рівняння
Звідки,
Знаходимо
Отже, загальний розв’язок неоднорідного рівняння має вигляд:
Використаємо початкові умови:
Розв’язок задачі Коші має вигляд:
Завдання для самостійного розв’язування
Знайти загальні розв’язки наступних диференціальних рівнянь.
1) 3) 5) Література 1. Вища математика: основні означення, приклади і задачі: У двох книгах/ За редакцією Г.Л.Кулініча та І.П.Васильченка.- К.: Либідь, 1994. 2. Дубовик В.П., Юрик І.І. Вища математика.- К.: Вища школа, 1993. 3. Богомолов М.В. Практичні заняття з математики.- К.: Вища школа, 1979. 4. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1.- М.:Наука, 1976. 5. Берман Г.Н. Сборник задач по курсу математического анализа.- М.: Наука, 1975. Зміст
ВСТУП…………………………………………………………………….3 1. Подвійний інтеграл, його властивості. Обчислення подвійного інтеграла в декартових координатах……………………………….….4 2. Обчислення подвійного інтеграла в полярній системі координат. Застосування подвійних інтегралів до задач геометрії……………...13 3. Застосування подвійного інтеграла для деяких задач механіки…...20 4. Обчислення криволінійних інтегралів першого та другого роду. Формула Гріна. Умови незалежності криволінійного інтеграла від шляху інтегрування…………………………………………………29 5. Звичайні диференціальні рівняння. Диференціальні рівняння першого порядку. ….…………………………………………………..38 6. Диференціальні рівняння вищих порядків. Диференціальні рівняння, що припускають зниження порядку……………………….58 7. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами…………………………………………………………..72 8. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами із спеціальною правою частиною…… …76 9. Метод варіації довільних сталих……………………………………89 Література………………………………………………………………95
Навчальне видання
Кадильникова Тетяна Михайлівна Щербина Ірина Володимирівна Хорошманенко Павло Григорович
ВИЩА МАТЕМАТИКА В ПРИКЛАДАХ ТА ЗАДАЧАХ Частина IV Навчальний посібник
Тем. план 2010, поз. 252
Підписано до друку 27.10.2010.Формат 60x84 1/16 Папір друк. Друк плоский. Облік.-вид.арк.5,65. Умов.друк арк.5,58. Тираж 100 пр. Замовлення №.
Національна металургійна академія України 49600, м. Дніпропетровськ – 5, пр. Гагаріна, 4 ___________________________________________ Редакційно- видавничий відділ НМетАУ
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.007 с.) |

 ,
,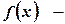 будь-яка функція.
будь-яка функція. ,
, частинні розв’язки відповідного диференціального однорідного рівняння, які знаходимо за таблицею 1,
частинні розв’язки відповідного диференціального однорідного рівняння, які знаходимо за таблицею 1,  функції, які є розв’язком системи рівнянь:
функції, які є розв’язком системи рівнянь:
 .
.
 та
та 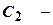 не довільні сталі, а деякі функції, які знайдемо із системи рівнянь:
не довільні сталі, а деякі функції, які знайдемо із системи рівнянь:
 ,
, .
. .
.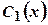 та
та  :
: ,
, .
. .
. .
.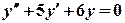 з характеристичним рівнянням
з характеристичним рівнянням 

 мають вигляд
мають вигляд  .
. , де невідомі функції
, де невідомі функції 
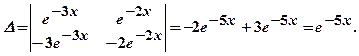 ,
,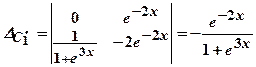 ,
, .
. .
. .
. .
. .
. .
.
 .
.

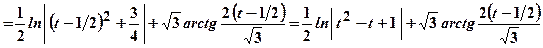 .
.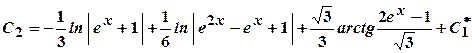 .
.
 .
. .
. відповідного однорідного диференціального рівняння має корені
відповідного однорідного диференціального рівняння має корені  , тому частинні розв’язки однорідного рівняння
, тому частинні розв’язки однорідного рівняння  .
.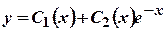 . Для знаходження невідомих функцій
. Для знаходження невідомих функцій 


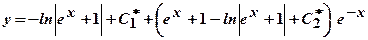 .
. .
. мають вигляд
мають вигляд  . Загальний розв’язок початкового рівняння дістанемо у вигляді
. Загальний розв’язок початкового рівняння дістанемо у вигляді  , де невідомі функції
, де невідомі функції  та
та  задовольняють системі алгебраїчних лінійних рівнянь:
задовольняють системі алгебраїчних лінійних рівнянь: або
або 
 ;
;
 ;
;  .
. ,
,  .
.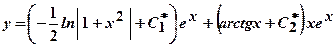 ,
,
 .
.
 .
. . 2)
. 2)  .
. . 4)
. 4)  .
. .
.


