
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Звичайні диференціальні рівняння. Диференціальне рівняння першого порядку.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Диференціальним рівнянням називають рівняння, яке зв’язує незалежну змінну
Порядок диференціального рівняння визначається найвищим порядком похідної (диференціала) цього рівняння. Розв’язком диференціального рівняння називається функція Диференціальне рівняння першого порядку має вигляд
де Якщо рівняння можна розв’язати відносно похідної, то його записують у вигляді
Розв’язком диференціального рівняння (5.1) на деякому інтервалі Функція 1) функція 2) для довільної точки
Частинним розв’язком рівняння (5.1) називається функція Якщо загальний розв’язок диференціального рівняння знайдено в неявному вигляді, тобто Види диференціальних рівнянь першого порядку: 1. Диференціальні рівняння з відокремлюваними змінними. 2. Однорідні диференціальні рівняння. 3. Лінійні диференціальні рівняння. 4. Диференціальні рівняння Бернуллі. Диференціальні рівняння з відокремлюваними змінними мають вигляд:
(5.2) де
Рівняння (5.3) називається рівнянням з відокремленими змінними. Інтегруючи обидві частини останнього рівняння отримаємо загальний інтеграл диференціального рівняння з відокремлюваними змінними:
Диференціальне рівняння (5.2) є окремим випадком рівняння виду:
Для відокремлення змінних у цьому рівнянні досить обидві його частини поділити на добуток Функція
Диференціальне рівняння
називається однорідним, якщо функція Підстановкою
Лінійним диференціальним рівнянням першого порядку називається рівняння виду
де Розв’язок рівняння (5.6) знаходимо у вигляді
де
Рівняння Бернуллі має вигляд
де При
Зразки розв’язування задач
Приклад 1. Розв’язати рівняння:
Розв’язання. Це рівняння є диференціальним рівнянням з відокремлюваними змінними. Для того, щоб відокремити змінні, поділимо обидві частини рівняння на
Для того, щоб обчислити інтеграл, що знаходиться у правій частині, використаємо заміну змінної в невизначеному інтегралі:
Маємо:
Повертаючись до старої змінної, дістанемо:
Приклад 2. Знайти загальний розв’язок диференціального рівняння:
Розв’язання. Вважаючи, що
Помножимо обидві частини на
Після інтегрування отримаємо:
Приклад 3. Розв’язати задачу Коші:
Розв’язання. Для того, щоб відокремити змінні, треба спочатку винести за дужки співмножники в кожній з частин рівняння, тобто
Підставимо початкові умови в загальний розв’язок та отримаємо частинний розв’язок рівняння
Приклад 4. Знайти частинний розв’язок рівняння
Розв’язання. Для відокремлювання змінних у цьому рівнянні розділимо його на
Проінтегруємо обидві частини рівняння та для обчислення інтегралів зробимо відповідні заміни змінних:
Використаємо початкові умови і отримаємо частинний розв’язок рівняння:
Приклад 5. Записати рівняння кривої, яка проходить через точку Розв’язання. Кутовий коефіцієнт дотичної до кривої
Вважаємо, що
Підставимо координати точки, через яку проходить шукана крива, в отриманий розв’язок:
Тоді
Приклад 6. Розв’язати рівняння:
Розв’язання. Доведемо, що це рівняння є однорідним. Нехай
Для того, щоб перетворити його на рівняння з відокремлюваними змінними, зробимо підстановку:
Відокремлюючи змінні, маємо
Після інтегрування отримаємо загальний інтеграл даного диференціального рівняння:
Приклад 7. Знайти загальний розв’язок:
Розв’язання. Маємо:
Функції
Тобто початкове рівняння є однорідним. Зробимо підстановку
Відокремимо змінні в останньому рівнянні:
Приклад 8. Розв’язати задачу Коші
Розв’язання. Це рівняння є однорідним (перевірити самостійно), тому після підстановки
Відокремимо змінні і проінтегруємо обидві частини рівняння:
або
Використаємо початкові умови:
Тоді
Приклад 9. Знайти частинний розв’язок рівняння:
Розв’язання. Маємо:
Це однорідне рівняння. Зробимо підстановку
Для обчислення інтеграла, що знаходиться у лівій частині, використаємо заміну змінної
Тоді, загальний інтеграл рівняння має вигляд
Приклад 10. Розв’язати рівняння:
Розв’язання. Це рівняння є лінійним, і його розв’язок будемо шукати у вигляді Маємо:
Будемо вважати, що вираз в дужках у лівій частині рівняння дорівнює нулю. Тоді отримаємо систему диференціальних рівнянь з відокремлюваними змінними:
Знайдемо, спочатку, розв’язок першого рівняння. Для цього відокремимо змінні та проінтегруємо рівняння:
Підставимо знайдений розв’язок в друге рівняння системи:
Тоді, шуканий розв’язок лінійного рівняння матиме вигляд:
Приклад 11. Розв’язати рівняння:
Розв’язання. Розв’язок цього лінійного рівняння знаходимо у вигляді
І.
ІІ.
Для останнього інтеграла використаємо підстановку:
Дістанемо: Тоді загальний розв’язок лінійного рівняння буде мати вигляд:
Приклад 12. Розв’язати рівняння:
Розв’язання. Розділимо рівняння на
І. ІІ. Отже,
Приклад 13. Розв’язати задачу Коші:
Розв’язання. Розділимо обидві частини рівняння на
Тоді
І.
ІІ.
Зробимо заміну змінної в інтегралі, що знаходиться праворуч.
Для останнього інтеграла використаємо метод інтегрування частинами:
Отже, повертаючись до старої змінної, отримаємо:
Тоді, загальний розв’язок лінійного рівняння має вигляд:
Підставимо в цей вираз початкові умови: Отже
Приклад 14. Розв’язати рівняння:
Розв’язання. Маємо рівняння Бернуллі, класичний вигляд якого буде:
Метод розв’язання – аналогічний до метода розв’язання лінійних рівнянь. Тобто, вважаючи, що
Нехай,
І.
ІІ. Для останнього інтеграла використаємо заміну змінної
Загальний розв’язок рівняння Бернуллі матиме вигляд:
Приклад 15. Розв’язати рівняння:
Розв’язання. Перепишемо це рівняння Бернуллі у класичному вигляді:
Загальний розв’язок рівняння Бернуллі буде
Після підстановки цих виразів в початкове рівняння маємо:
І. ІІ.
Отже, загальний розв’язок рівняння:
Приклад 16. Розв’язати задачу Коші:
Розв’язання. Загальний розв’язок рівняння Бернуллі будемо шукати у вигляді:
Тоді: І.
ІІ.
Отже загальний розв’язок рівняння Бернуллі має вигляд:
Використовуючи початкові умови знайдемо сталу
Маємо частинний розв’язок рівняння Бернуллі:
Приклад 17. Розв’язати задачу Коші:
Розв’язання.
Аналогічно попередньому прикладу загальний розв’язок задачі шукаємо у вигляді
І.
ІІ.
Тоді, загальний розв’язок даного рівняння має вигляд:
Для визначення частинного розв’язку знаходимо
Тому, частинний розв’язок має вигляд:
Завдання для самостійної роботи І. З’ясувати чи будуть функції а) б) в)
ІІ. Знайти загальні інтеграли рівнянь:
1) 2) 3) 4)
ІІІ. Знайти частинні розв’язки диференціальних рівнянь: 1) 2) 3) 4) 5) 6) 7)
8) IV. Записати рівняння кривої, яка проходить через точку 1) 2) 3)
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.009 с.) |

 , шукану функцію
, шукану функцію 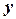 та її похідні (або диференціали):
та її похідні (або диференціали): , або
, або .
. , яка при підстановці у це рівняння перетворює його на тотожність.
, яка при підстановці у це рівняння перетворює його на тотожність. , (5.1)
, (5.1) незалежна змінна,
незалежна змінна,  шукана функція,
шукана функція,  похідна шуканої функції.
похідна шуканої функції. .
. називається диференційована на цьому інтервалі функція
називається диференційована на цьому інтервалі функція  , яка при підстановці в рівняння (5.1) перетворює його на тотожність на
, яка при підстановці в рівняння (5.1) перетворює його на тотожність на 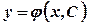 , де
, де  довільна стала, називається загальним розв’язком рівняння (5.1) в області
довільна стала, називається загальним розв’язком рівняння (5.1) в області  , якщо вона задовольняє дві умови:
, якщо вона задовольняє дві умови: є розв’язком рівняння при будь-якому значенні сталої
є розв’язком рівняння при будь-якому значенні сталої  з деякої множини;
з деякої множини; можна знайти таке значення
можна знайти таке значення  , що функція
, що функція  задовольняє початкову умову:
задовольняє початкову умову: .
. , то такий розв’язок називають загальним інтегралом диференціального рівняння (5.1).
, то такий розв’язок називають загальним інтегралом диференціального рівняння (5.1).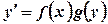 ,
, і
і  задані і неперервні на деякому інтервалі функції. Вважаючи, що
задані і неперервні на деякому інтервалі функції. Вважаючи, що  , дістанемо
, дістанемо або
або  ,
,  . (5.3)
. (5.3) .
. (5.4)
(5.4) ,
,  .
.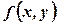 називається однорідною функцією
називається однорідною функцією  го виміру відносно змінних
го виміру відносно змінних 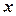 та
та  виконується тотожність:
виконується тотожність: .
. (5.5)
(5.5) .
.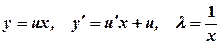 , де
, де  невідома функція, рівняння (5.5) зводиться до рівняння з відокремленими змінними:
невідома функція, рівняння (5.5) зводиться до рівняння з відокремленими змінними: .
.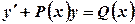 , (5.6)
, (5.6) та
та  задані і неперервні на деякому проміжку функції.
задані і неперервні на деякому проміжку функції. , (5.7)
, (5.7) та
та  невідомі функції, причому одна з них функція довільна (але не дорівнює тотожно нулю). Після підстановки (5.7) в рівняння (5.6) рівняння (5.6) перетворюється на систему 2-х рівнянь з відокремлюваними змінними.
невідомі функції, причому одна з них функція довільна (але не дорівнює тотожно нулю). Після підстановки (5.7) в рівняння (5.6) рівняння (5.6) перетворюється на систему 2-х рівнянь з відокремлюваними змінними. , (5.8)
, (5.8) .
. рівняння (5.8) буде лінійним, при
рівняння (5.8) буде лінійним, при  рівнянням з відокремлюваними змінними. Метод розв’язання рівняння Бернуллі такий саме як і для лінійного рівняння, тобто розв’язок його знаходимо у вигляді
рівнянням з відокремлюваними змінними. Метод розв’язання рівняння Бернуллі такий саме як і для лінійного рівняння, тобто розв’язок його знаходимо у вигляді  .
. .
. , а потім проінтегруємо його:
, а потім проінтегруємо його: ,
, ,
, .
. ,
,
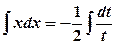 , або
, або  .
. ,
,  загальний розв’язок рівняння.
загальний розв’язок рівняння. .
. , маємо:
, маємо: .
.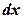 , а потім відокремимо змінні. Для цього рівняння розділимо на
, а потім відокремимо змінні. Для цього рівняння розділимо на 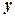 :
: .
. ,
, ,
,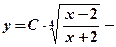 загальний розв’язок.
загальний розв’язок.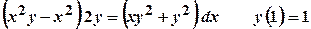 .
.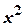 та
та  з лівої і правої частин рівняння відповідно, а потім розділити рівняння на
з лівої і правої частин рівняння відповідно, а потім розділити рівняння на  і проінтегрувати
і проінтегрувати
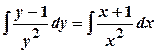 ,
, ,
, ,
, загальний розв’язок.
загальний розв’язок. ,
, частинний розв’язок.
частинний розв’язок. .
. . Маємо:
. Маємо: .
. ,
, ,
, ,
, , або
, або 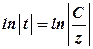 ,
, або
або  .
. загальний розв’язок.
загальний розв’язок.
 , кутовий коефіцієнт дотичної до якої у кожній точці дорівнює
, кутовий коефіцієнт дотичної до якої у кожній точці дорівнює  .
.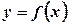 у кожній точці є
у кожній точці є 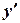 . Маємо диференціальне рівняння з відокремлюваними змінними:
. Маємо диференціальне рівняння з відокремлюваними змінними: .
. ,
, ,
, ,
,
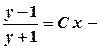 загальний розв’язок рівняння.
загальний розв’язок рівняння. .
. є рівнянням цієї кривої.
є рівнянням цієї кривої. .
. 
 , тоді
, тоді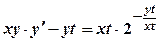 ,
, , тобто рівняння однорідне.
, тобто рівняння однорідне. . Отримаємо:
. Отримаємо: , або
, або  ,
, .
.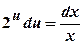 .
. ,
, .
. .
. .
. та
та  є однорідними функціями другого виміру:
є однорідними функціями другого виміру: ;
; ,
, , та зведемо це рівняння до рівняння з відокремлюваними змінними:
, та зведемо це рівняння до рівняння з відокремлюваними змінними: ,
, ,
, , або
, або .
. ;
; ;
; ;
; , або
, або загальний інтеграл даного рівняння;
загальний інтеграл даного рівняння; ,
, ,
, ,
, загальний розв’язок рівняння.
загальний розв’язок рівняння. .
. ,
,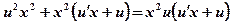 , або
, або  ,
,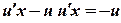 ,
, ,
, .
. ,
, ,
,  ,
, загальний інтеграл.
загальний інтеграл.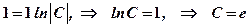 .
. , або
, або 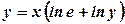 , або
, або  розв’язок задачі Коші.
розв’язок задачі Коші. при
при  .
. .
.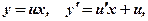
 та аналогічно попереднім прикладам розв’яжемо отримане рівняння:
та аналогічно попереднім прикладам розв’яжемо отримане рівняння: ,
,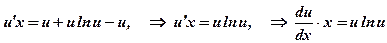 ,
, .
. . Маємо:
. Маємо:
 .
. . Знайдемо
. Знайдемо  .
. частинний розв’язок рівняння.
частинний розв’язок рівняння. .
.
 ,
,  .
.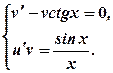

 .
.
 .
. .
. .
. . Після підстановки цих виразів в лінійне рівняння і розв’язування його аналогічно попередньому дістанемо:
. Після підстановки цих виразів в лінійне рівняння і розв’язування його аналогічно попередньому дістанемо: ,
, .
.

 .
.
 .
. .
. .
. .
. .
.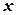 , та розв’яжемо його аналогічно попередньому:
, та розв’яжемо його аналогічно попередньому:  ;
;  ;
; ,
,  ,
,

 .
.
 .
. загальний розв’язок.
загальний розв’язок. .
. . Дістанемо:
. Дістанемо: .
.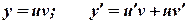 ,
, ,
,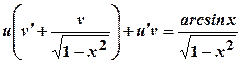 .
.
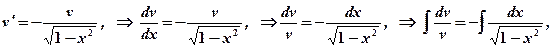
 ;
;
 .
. .
.
 .
. .
. , або
, або .
. .
.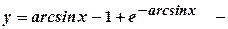 частинний розв’язок лінійного рівняння.
частинний розв’язок лінійного рівняння. .
.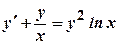 .
. ,
,  .
.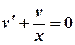 , тоді
, тоді 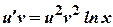 або
або  . Таким чином, одержимо систему рівнянь з відокремлюваними змінними:
. Таким чином, одержимо систему рівнянь з відокремлюваними змінними:

 .
. .
. . Дістанемо:
. Дістанемо: 
 .
. , або
, або  .
. .
. .
. .
. ,
, .
.
 .
.
 .
. .
. .
. ,
, .
. або
або 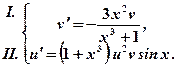
 .
.
 .
.
 .
. .
. .
.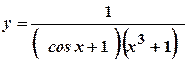 .
. .
. . Маємо:
. Маємо:




 .
.



 .
.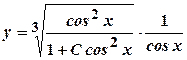 , або
, або  .
. .
.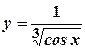 .
. ;
; ;
; .
. ; 5)
; 5)  ;
; ; 6)
; 6)  ;
; ; 7)
; 7)  ;
;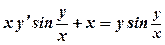 ; 8)
; 8)  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; , кутовий коефіцієнт дотичної до якої дорівнює
, кутовий коефіцієнт дотичної до якої дорівнює 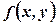 .
. ;
; ;
;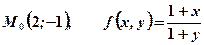 .
.


