
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні рівняння другого порядку.Содержание книги
Поиск на нашем сайте
Задача 1. 1. Рівнянням 2-го порядку називається рівняння, що пов’язує незалежну змінну,невідому функцію і її перші дві похідні: F (x, y, у /, у //) = 0. В багатьох випадках можна розв’язати це рівняння відносно старшої похідної: y // = f (x, y, y). 2. Задача знаходження такого розв’язку рівняння, що задовольняє початковим умовам у (х 0) = у 0, у ' (х 0) = у 1 називається задачею Коші. 3. Загальним розв’язком рівняння другого порядку називається функція у = φ (х, С 1, С2) така, що: 1. при будь-яких довільних сталих С 1, С2 перетворює дане рівняння в тотожність; 2. при будь-яких початкових умовах знайдуться такі значення довільних сталих С 1*, С2 *, при яких φ (х 0, С 1*, С2 *) = у 0. 4. Будь-яка функція у = φ (х, С 10, С2 0), яка отримана із загального розв’язку при конкретних значеннях сталих С 1, С2 називається частинним розв’язком. 5. Дане рівняння, не містить явно шукану функцію у(х): F (x, y ', y)=0. Можна знизити порядок рівняння підстановкою у ' = р (х), у '' = р ' (х), де р (х) – нова невідома функція. 6. Підставивши вирази у ' = р (х), у '' = р ' (х) в дане рівняння, після спрощень отримаємо диференціальне рівняння першого порядку відносно функції р (х) (див. частину ІV). 7. Розв’язавши отримане рівняння, знайдемо функцію р (х). Робимо зворотну підстановку у ' = р (х). Отримаємо диференціальне рівняння першого порядку відносно функції у(х). Розв’язавши це рівняння, отримаємо загальний розв’язок даного диференціального рівняння другого порядку. 8. Для знаходження розв’язку задачі Коші знайдемо похідну 9. Розв’язавши систему з п.8, підставимо знайдені значення коефіцієнтів Задача 2. 1. Рівняння другого порядку, що не містить явно незалежну змінну х: F (у, y ', y '')=0. В такому рівнянні можна знизити порядок підстановкою у ' = р (у), у '' = р ' (у) · р (у), де р (у) – нова невідома функція. 2. Підставивши замість у ', у '' їх вирази, отримаємо диференціальне рівняння першого порядку. 3. Розв’язуємо отримане рівняння, робимо зворотну підстановку і маємо ще одне диференціальне рівняння першого порядку. Розв’язавши його, знайдемо загальний розв’язок диференціального рівняння другого порядку.
Задачі 3, 4, 5. 1. Дані лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами (ЛНДР ІІ). Алгоритм їх розв’язання наведено в задачі 5 частини ІV даного посібника. 2. Для знаходження розв’язку задачі Коші в рівнянні 5 знайдемо похідну 3. Розв’язавши систему з п.2, підставимо знайдені значення коефіцієнтів VІ. Ряди. Задача 1. 1. Числовим рядом називається символ
де числа а 1, а 2, а 3,… називаються членами ряду, член аn – загальним членом ряда. 2. Сума n перших членів ряду називається n -ою частинною сумою ряду і позначається
3. Числовий рядназивається збіжним, якщо існує скінчена границя послідовності його частинних сум
Число S називається сумою ряду. Якщо така границя не існує або дорівнює нескінченності, то ряд називається розбіжним. 4. Необхідна умова збіжності ряду. Якщо числовий ряд збігається, то загальний член ряду прямує до нуля при n → ∞:
Дана умова є тільки необхідною, але не достатньою для збіжності ряду. Якщо 5. Якщо при всіх n виконується нерівність аn ≥ 0, то він називається рядом з невід’ємними членами. Якщо аn > 0 при всіх n, то маємо ряд з додатними членами. 6. Ознака Даламбера. Нехай ряд
Тоді, при l > 1 ряд розбігається, при l < 1 ряд збігається, при l = 1 треба досліджувати ряд за допомогою інших ознак. 7. Ознаку Даламбера зручно використовувати, коли загальний член ряду містить факторіали, показникові функції.
Задача 2. 1. Ряд, що містить і додатні і від’ємні члени називається знакозмінним. 2. Частинним випадком знакозмінних рядів є знакопереміжні ряди. Ряд, в якому будь-які два сусідні члени мають різні знаки, називаються знакопереміжними:
або де а 1, а 2, …, аn, … – додатні дійсні числа.
3. Знакопереміжні ряди досліджують на збіжність за ознакою Лейбніца. Нехай даний знакопереміжний ряд 1) абсолютні величини членів ряду монотонно спадають (а 1 > а 2 > а 3>…) і 2) загальний член ряду прямує до нуля при n → ∞ ( 4. Якщо хоча б одна з умов не виконується, то ряд розбігається. Задача 3. 1. Ряд, членами якого є функції, називається функціональним:
причому, всі функції повинні бути визначені і неперервні в одному інтервалі. 2. Якщо в функціональний ряд замість х підставити конкретне значення х = х 0, то він стане числовим. Для одних значень х ряд може збігатися, для інших – розбігатися. 3. Значення х = х 0, при яких числовий ряд 4. Частиннимвипадком функціонального ряду є степеневий ряд, тобто ряд вигляду де а 0, а 1, …, аn, … числа, які називаються коефіцієнтами степеневого ряду. 5. При х 0 = 0 степеневий ряд має вигляд 6. Всі степеневі ряди збігаються при 7. Для дослідження степеневого ряду на збіжність треба знайти радіус та інтервал збіжності. 8. Радіусом збіжності степеневого ряду називається таке число R, що для всіх х таких, що 9. Радіус збіжності степеневого ряду знаходиться за формулою:
10. Інтервалом збіжності степеневого ряду називається інтервал (х 0 – R; х 0 + R). 11. Якщо степеневий ряд збігається при всіх х, то вважають, що R = ∞. Якщо ряд розбігається при всіх х, крім х = 0, то вважають R = 0. 12. На кінцях інтервалу збіжності (при Задача 4. 1. Якщо функція f(x) диференційована в околі деякої точки де а 0, а 1, а 2, а 3, …, аn, …– коефіцієнти ряду. 2. Ряд вигляду 3. Щоб розкласти функцію f (х) в ряд Тейлора в околі даної точки треба знайти похідні функції до n- го порядку, обчислити значення похідних в точці
Задача 5. 1. Ряд, який отриманий з ряду Тейлора при х 0 = 0, називається рядом Маклорена і має вигляд:
2. Ряд Тейлора при х 0 = 0 є розвиненням функції за степенями х. 3. Розвинення в ряд Тейлора при х 0 = 0 деяких елементарних функцій. 1. 2. 3.
4.
5. 6. Література. 1. Пак В.В, Носенко Ю.Л. Вища математика. – К.: Либідь,1996. 2. Улітін Г.М., Гончаров А.Н. Курс лекцій з вищої математики. – Донецьк: ДонНТУ, 2009. 3. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1975. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах (части 1,2). – М.: Высшая школа, 1999. 5. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. В 2-х ч. – М. Айрис пресс, 2004. – 590 с.
Зміст. Вступ. …………………………………………………………………………….. 4
Загальне формулювання задач. …………………………………………………. 5 І. Невизначений інтеграл. ……………………………………………………….. 5 ІІ. Визначений інтеграл. …………………………………………………………. 5 ІІІ. Функції багатьох змінних. …………………………………………………… 5 ІV. Диференціальні рівняння. …………………………………………………… 5 V. Диференціальні рівняння другого порядку. …………………….………… 6 VІ. Числові та функціональні ряди. ………………………………………… 6 Варіанти домашніх індивідуальних завдань. ………………………………… 7 Варіант 1. ……………………………………………………………………… 7 Варіант 2. ……………………………………………………………………… 9 Варіант 3. ……………………………………………………………………… 11 Варіант 4. ……………………………………………………………………… 13 Варіант 5. ……………………………………………………………………… 15 Варіант 6. ……………………………………………………………………… 17 Варіант 7. ……………………………………………………………………… 19 Варіант 8. ……………………………………………………………………… 21 Варіант 9. ……………………………………………………………………… 23 Варіант 10.……………………………………………………………………… 25 Варіант 11. ….. ………………………………………………………………… 27 Варіант 12. …………………………………………………………………….. 29 Варіант 13. …………………………………………………………………….. 31 Варіант 14. …………………………………………………………………… … 33 Варіант 15. …………………………………………………………………….. 35 Варіант 16. …………………………………………………………………….. 37 Варіант 17. …………………………………………………………………….. 39 Варіант 18. …………………………………………………………………….. 41 Варіант 19. …………………………………………………………………….. 43 Варіант 20. …………………………………………………………………….. 45 Варіант 21. …………………………………………………………………….. 47 Варіант 22. …………………………………………………………………….. 49 Варіант 23. …………………………………………………………………….. 51 Варіант 24. …………………………………………………………………….. 53 Варіант 25. …………………………………………………………………….. 55 Довідкові матеріали. ………………………………………………………….. 57 І. Невизначений інтеграл. ………….……………………………………… 57 ІІ. Визначений інтеграл. ………………………………………………………. 61 ІІІ. Функції багатьох змінних. ……………………………………………….. 64 ІV. Диференціальні рівняння. ………………………………………………… 68 V. Диференціальні рівняння другого порядку. …………………….………… 72 VІ. Числові та функціональні ряди. ………………………………..………… 74 Література. ……………………………………………………………………… 80
Зміст. ……………………………………………………………………………. 81
Домашні індивідуальні завдання з вищої математики: методичний посібник для самостійної роботи студентів. (для студентів всіх спеціальностей) Частина ІІ.
Укладачі Гребьонкіна Олександра Сергіївна Євсеєва Олена Геннадіївна Кльоміна Світлана Іванівна Савін Олександр Іванович
Рекомендовано до видання навчально-методичною радою ДонНТУ. Протокол № 6 від 06.10.11 Ум. друк. с. 3,5.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.206.104 (0.008 с.) |

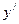 . Потім підставимо в у і
. Потім підставимо в у і  ,
,  і
і 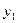 відповідно. Виконавши обчислення, отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих коефіцієнтів
відповідно. Виконавши обчислення, отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих коефіцієнтів  .
. і
і  в у(х). Отриманий розв’язок є частинним розв’язком даного диференціального рівняння.
в у(х). Отриманий розв’язок є частинним розв’язком даного диференціального рівняння. . Потім підставимо в узн і
. Потім підставимо в узн і 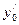 відповідно. Виконавши обчислення, отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих коефіцієнтів
відповідно. Виконавши обчислення, отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих коефіцієнтів  . Отриманий розв’язок є частинним розв’язком ЛНДР ІІ.
. Отриманий розв’язок є частинним розв’язком ЛНДР ІІ. ,
,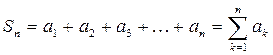 .
. :
: .
. .
. , то ряд розбігається. Якщо ж
, то ряд розбігається. Якщо ж 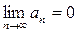 , то ряд може як збігатися, так і розбігатися.
, то ряд може як збігатися, так і розбігатися. – ряд з додатними членами і існує скінчена границя
– ряд з додатними членами і існує скінчена границя .
.

 або
або 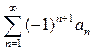 . Якщо:
. Якщо: ), то ряд збігається.
), то ряд збігається.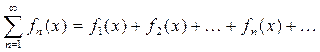 ,
,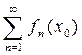 збігається, називається точкою збіжності функціонального ряду. Множина всіх точок збіжності функціонального ряду називається областю його збіжності.
збігається, називається точкою збіжності функціонального ряду. Множина всіх точок збіжності функціонального ряду називається областю його збіжності. ,
,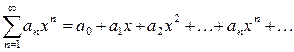
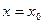 .
. < R, ряд збігається абсолютно, а для всіх х таких, що
< R, ряд збігається абсолютно, а для всіх х таких, що  .
. і
і  ) необхідно провести додаткове дослідження. Ряд може збігатися в обох точках, або тільки в одній з них, або розбігатися в обох. Для дослідження треба підставити значення
) необхідно провести додаткове дослідження. Ряд може збігатися в обох точках, або тільки в одній з них, або розбігатися в обох. Для дослідження треба підставити значення 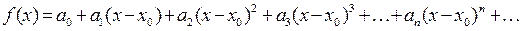 ,
, називається рядом Тейлора функції f (х). Коефіцієнти
називається рядом Тейлора функції f (х). Коефіцієнти  називаються коефіцієнтами Тейлора функції f (х) в точці х 0.
називаються коефіцієнтами Тейлора функції f (х) в точці х 0.
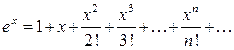 (х
(х  R)
R) (х
(х  (х
(х 
 (х
(х  (х
(х  (х
(х 


