
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ІV. Диференціальні рівняння.Содержание книги
Поиск на нашем сайте
Задача 1. 1. Рівняння, які зв’язують невідому функцію, її диференціали або похідні та аргумент, називаються диференціальними (ДР). Коли невідома функція залежить лише від одного аргументу, тоді ДР називається звичайним. 2. Найвищий порядок похідної, що входить в ДР, називається порядком ДР. 3. Рівняння, яке пов’язує незалежну змінну х, невідому функцію у (х) та її похідну y ', називається ДР першого порядку: F (x, y, y ') = 0 або y ' = f (х, у). 4. Розв’язком ДР першого порядку називається будь-яка функція у = φ (х), яка при підстановці її разом з похідною в рівняння, перетворює його в тотожність. Графік функції у = φ (х) називається інтегральною кривою. 5. Розв’язок ДР, який задовольняє початковій умові у (х 0) = у 0 , називається частинним розв’язком. 7. Задачу пошуку розв’язку ДР першого порядку, який задовольняє даній початковій умові, називають задачею Коші:
8. Загальним розв’язком ДР першого порядку називається така функція у = φ (х, С), де С – довільна стала, що: 1. при будь-якому значенні С вона є розв’язком цього рівняння; 2. для будь-якої припустимої початкової умови у (х 0) = у 0 знайдеться таке значення сталої С = С 0, що φ (х 0, С 0) = у 0. 9. ДР вигляду M 1(х) N 1(у) dx + M 2(х) N 2(у) dy = 0 (або y ' = f 1(х) f 2(у)) називається рівнянням з відокремлюваними змінними. Щоб розв’язати таке рівняння, необхідно поділити обидві його частини на множник N 1(у) M 2(х) ≠ 0 (або на f 2 (у) ≠ 0), а потім проінтегрувати отримане рівняння. В результаті знайдемо загальний розв’язок рівняння. 10. Для знаходження частинного розв’язку слід замість х і у підставити в загальний розв’язок значення
Задача 2. 1. ДР першого порядку y ' = f (х, у) називається однорідним, якщо функцію f (х, у) можна привести до вигляду f (х, у)= називається однорідною відносно своїх аргументів. 2. Розв’язок однорідного ДР шукають у вигляді y=z(x)x, де z(x) – нова невідома функція. В загальному випадку в однорідному ДР відокремити змінні неможливо. 3. Якщо y=zx, то y ' = z ' x + z. Підставивши y та y ' в дане однорідне рівняння і виконавши тотожні перетворення, отримаємо ДР першого порядку з відокремлюваними змінними (див. задачу 1).
Задача 3. 1. ДР вигляду y ' + p (x) y = g (x), де p (x), g (x) – дані неперервні функції, називається лінійним. 2. Розв’язок рівняння шукають у вигляді у = u (х) v (х). Одну з функцій u, v обирають довільно (як правило v (х)). Іншу – в залежності від першої так, щоб їх добуток був розв’язком рівняння. 3. Якщо у = иv, то у ' = u ' v + uv ', а рівняння приймає вигляд: u ' v + u (v ' + p (x) v) = g (x). 4. Функцію v (х) вибирають так, щоб вираз в дужках був рівним нулю: v ' + p (x) v = 0. Тоді для знаходження и (х) маємо рівняння u ' v = g (x). Отже, отримали систему рівнянь з відокремлюваними змінними для знаходження u, v:
5. Розв’язавши цю систему, знайдемо функції и (х) і v (х). Загальний розв’язок лінійного рівняння отримаємо, як добуток знайдених функцій: у = иv. 6. Частинний розв’язок лінійного ДР знаходять так само, як і у випадку ДР з відокремлюваними змінними(див. задачу 1).
Задача 4. 1. Рівняннявигляду y '' + а 1 y ' + а 2 y = 0, де 2. Загальний розв’язок узо = С 1 у 1 + С 2 у 2, де
3. Розв’язок ЛОДР ІІ шукають у вигляді у = еkx. Тоді у ' = kеkx, у '' = k 2 еkx. Підставивши похідні в ЛОДР ІІ і скоротивши на еkx, отримаємо рівняння: k 2 + а 1 k + а 2 = 0. Таке рівняння є характеристичним рівнянням для ЛОДР ІІ. В залежності від його коренів ф.с.р. і загальний розв’язок ЛОДР ІІ приймають один з наступних виглядів. 4. Нехай характеристичне рівняння має два різних дійсних кореня k 1 ≠ k 2. Тоді узо = С 1 5. Нехай характеристичне рівняння має два однакових дійсних кореня k 1= k 2= k. Тоді у зо = еkx (С 1 + С 2 х), С 1, С 2 6. Нехай характеристичне рівняння має два комплексних спряжених кореня k 1,2 = α ± βі. Тоді ф. с. р. утворюють функції у зо = е α x (С 1 Задача 5. 1. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами (ЛНДР ІІ) – це рівняння вигляду y '' + а 1 y ' + а 2 y = f (x), де f(x) – довільна неперервна функція.
2. Загальний розв'язок узн ЛНДР ІІ має вигляд узн = узо + уч, де узо – загальний розв'язок відповідного однорідного рівняння, уч – деякий частинний розв'язок даного неоднорідного рівняння. 3. Для розв’язання ЛНДР ІІ необхідно спочатку знайти загальний розв’язок 4. Якщо права частина рівняння f(x) має спеціальний вигляд, то частинний розв’язок уч шукаємо методом невизначених коефіцієнтів. 5. Деякі спеціальні праві частини і відповідні їм частинні розв’язки рівняння наведені в наступній таблиці:
6. Для знаходження розв’язку уч треба вибрати відповідний вигляд розв’язку з таблиці, знайти похідні 7. Визначені в п.6коефіцієнти підставимо в частинний розв’язок уч. Загальний розв’язок Частина V.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.225 (0.007 с.) |

 – задача Коші.
– задача Коші. і
і  відповідно. Отримаємо конкретне числове значення
відповідно. Отримаємо конкретне числове значення  довільної сталої С. Підставивши це значення в загальний розв’язок рівняння, записуємо його частинний розв’язок.
довільної сталої С. Підставивши це значення в загальний розв’язок рівняння, записуємо його частинний розв’язок. . В цьому випадку функція f (х, у)
. В цьому випадку функція f (х, у)
 – числа, y(x) – невідома функція, називається лінійним однорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами (ЛОДР ІІ).
– числа, y(x) – невідома функція, називається лінійним однорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами (ЛОДР ІІ). ЛОДР ІІ має вигляд:
ЛОДР ІІ має вигляд: - довільні сталі,
- довільні сталі, - два будь-які лінійно незалежні розв’язки ЛОДР ІІ. Ці розв’язки утворюють так звану фундаментальну систему розв’язків (ф. с. р.).
- два будь-які лінійно незалежні розв’язки ЛОДР ІІ. Ці розв’язки утворюють так звану фундаментальну систему розв’язків (ф. с. р.). ,
,  . Загальний розв'язок ЛОДР ІІ:
. Загальний розв'язок ЛОДР ІІ: + С 2
+ С 2  , С 1, С 2
, С 1, С 2  R.
R. , а в якості другого розв'язку беремо
, а в якості другого розв'язку беремо 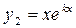 . Загальний розв'язок ЛОДР ІІ:
. Загальний розв'язок ЛОДР ІІ: і
і  , а загальний розв'язок ЛОДР ІІ має вигляд:
, а загальний розв'язок ЛОДР ІІ має вигляд: + С 2
+ С 2  ), С 1, С 2
), С 1, С 2  ,
де S = 0, якщо k 1 ≠ а і k 2 ≠ а,
S = 1, якщо k 1 = а або k 2 = а,
S = 2, якщо k 1 = k 2 = а;
Qn (х) – многочлен степеня n з невизначеними коефіцієнтами.
,
де S = 0, якщо k 1 ≠ а і k 2 ≠ а,
S = 1, якщо k 1 = а або k 2 = а,
S = 2, якщо k 1 = k 2 = а;
Qn (х) – многочлен степеня n з невизначеними коефіцієнтами.

 ,
де S = 1, якщо k 1,2 = ± bi,
S = 0 в інших випадках;
А, В – невизначені коефіцієнти.
,
де S = 1, якщо k 1,2 = ± bi,
S = 0 в інших випадках;
А, В – невизначені коефіцієнти.
 і підставити уч,
і підставити уч,  ЛНДР ІІ отримаємо склавши розв’язки
ЛНДР ІІ отримаємо склавши розв’язки 


