
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V. Диференціальні рівняння другого порядкуСодержание книги
Поиск на нашем сайте
1. 2. 3. 4. 5.
VI. Числові і функціональні ряди 1. а) 2. а) 3. а) 4. 5.
ВАРІАНТ №25 Частина 1 І. Невизначений інтеграл 1. а) 2. а) 3. а) 4. а) 5. а) ІІ. Визначений інтеграл 1. а) 2. 3. а) 4. 5. ІІІ. Функції багатьох змінних 1. 2. 3. 4. 5.
Частина 2 IV. Диференціальні рівняння 1. 2. 3. 4. а) в) 5.
V. Диференціальні рівняння другого порядку 1. 2. 3. 4. 5.
VI. Числові і функціональні ряди 1. а) 2. а) 3. а) 4. 5.
Довідкові матеріали. Частина 1. І. Невизначений інтеграл. Задача 1. 1. Функція F (х) називається первісною від функції f (х) на відрізку [ a, b ], якщо в усіх точках відрізку виконується рівність F ' (х) = f (х). 2. Множина усіх первісних F (х) + С для функції f (х) на відрізку [ a, b ] називається невизначеним інтегралом від f (х) і позначається
Функція f (х) називається підінтегральною функцією, вираз f (х) dx – підінтегральним виразом, х – змінною інтегрування, 3. Таблиця основних невизначених інтегралів. 1. 2. 3. 4. 5. 6. 7. 8. 4. Властивості невизначеного інтеграла. 1. Похідна невизначеного інтеграла дорівнює підінтегральній функції:
2. Постійний множник можна виносити за знак інтеграла:
3. Невизначений інтеграл від алгебраїчної суми скінченого числа функцій дорівнює алгебраїчній сумі інтегралів від функцій, що додаються:
4. Якщо
Задача 2. 1. Якщо при знаходженні інтеграла dх = φ ' (t) dt і виконується рівність:
2. Підстановку х = φ (t) необхідно підбирати так, щоб інтеграл в правій частині формули був табличним або легко зводився до табличного. 3. Після знаходження інтеграла 4. В багатьох інтегралах підстановку більш зручно зробити у вигляді t = φ (х); тоді dt = φ ' (х) dх.
Задача 3. 1. Якщо підінтегральний вираз можна записати у вигляді добутку udv, де u(x)
i v(x) – функції, які мають неперервні похідні, то має місце формула інтегрування частинами:
2. Записати підінтегральний вираз у вигляді добутку udv можна декількома способами. Причому, множник dv обов’язково містить диференціал змінної інтегрування. Після вибору множників u і dv треба диференціюванням знайти du та інтегруванням – v. При обчисленні Розглянемо основні типи інтегралів, які легко обчислити інтегруванням частинами. 3. В інтегралах вигляду 4. В інтегралах вигляду 5. В інтегралах вигляду 6. Метод інтегрування частинами можна, у разі необхідності, застосовувати декілька разів поспіль або комбінуючи з іншими методами інтегрування. Задача 4. 1. Інтеграли вигляду
2. Підстановка Задача 5. 1. Позначимо R (sin x, cos x) функцію зі змінними sin x та cos x, над якими виконані дії додавання, віднімання, множення або ділення (R – знак раціональної функції). 2. Будь-який інтеграл виду
Така підстановка називається універсальною тригонометричною підстановкою. В ряді випадків при інтегруванні тригонометричних функцій можна скористатися більш простими підстановками. Зокрема, однією з наступних, в залежності від вигляду підінтегральної функції. 3. В інтегралах 4. Коли інтеграл має вигляд 5. Інтеграл вигляду 5.1. коли n – ціле додатне непарне число, такий інтеграл можна спростити підстановкою t = sin х;
5.2. підстановку t = cos х використовують, коли m – ціле додатне непарне число; 5.3. якщо m і n – цілі невід’ємні парні числа, то для спрощення інтеграла можна застосувати формули зниження степеня тригонометричних функцій:
5.4. коли (m + n) – ціле від’ємне парне число, то використовують підстановку tg x = t. 6. Інтеграли вигляду
ІІ. Визначений інтеграл. Задача 1. 1. Найпростішим методом обчислення визначеного інтеграла є формула Ньютона-Лейбніца:
де F (х) – будь-яка первісна від функції f (х). 2. Метод заміни змінної використовують тоді, коли можна вибрати таку функцію x = g (t), що після підстановки підінтегральна функція стане простішою. Якщо при обчисленні інтеграла
де α, β – нові межі інтегрування, що знаходять із рівностей a = g (α), b = g (β). 3. При обчисленні визначеного інтеграла необхідно обов’язково перерахувати межі інтегрування. Повертатися до старої змінної не треба. Задача 2. 1. Формула інтегрування частинами для визначеного інтеграла має вигляд:
2. Множники u (х) і dv обираються так само, як в невизначеному інтегралі.
Задача 3. 1. Нехай функція f (х) інтегрована на будь-якому відрізку [ a; b ], тоді інтеграли
називаються невласними інтегралами першого роду. 2. Якщо границі в правих частинах формул скінчені, то інтеграли називаються збіжними. Якщо ці границі не існують або дорівнюють нескінченості, то інтеграли є розбіжними.
Задача 4. 1. Площа криволінійної трапеції, обмеженої графіком функції у = f (х) ³ 0, віссю О х і прямими х = а, х = b (рис. 1 а), обчислюється за формулою:
Рис. 1. 2. Якщо f (х) < 0 на [ a; b ], то 3. Якщо фігура обмежена зверху графіком функції у = f 2(х), знизу – у = f 1(х), зліва і справа прямими х = а, х = b відповідно (рис. 1 б), то її площа обчислюється за формулою:
4. Якщо фігура обмежена зверху лінією, що задана параметричними рівняннями х = х (t), у = у (t) > 0, t
причому х (t 1) = а, х (t 2) = b.
Задача 5. 1. Нехай криволінійна трапеція (рис. 1 а) обертається навколо осі О х. Тоді об’єм тіла обертання дорівнює:
2. Об’єм тіла, що утворене обертанням навколо осі О у фігури, яка обмежена лініями у = с, у = d, х = 0, х = g(у), обчислюється за формулою:
3. Якщолінія, що обмежує криволінійну трапецію, задана параметричними рівняннями х = х (t), у = у (t), t
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.89.242 (0.008 с.) |

 ,
,  ,
,  ;
;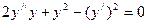 ;
; ;
; ;
; ,
,  ,
,  .
. , б)
, б)  .
. б)
б)  .
.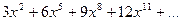 , б)
, б)  .
. ,
,  .
. .
. ; б)
; б)  .
.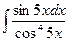 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  .
. .
. ; б)
; б)  .
. .
. .
. .
. ;
;  .
. .
. ;
;  .
. ;
;  ;
;  .
.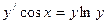 ,
,  ;
; ;
; ,
,  ; б)
; б) 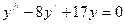 ;
; ,
,  ,
,  ;
; .
. ;
; ;
;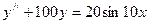 ;
; ,
,  ,
,  .
. , б)
, б)  .
. б)
б)  .
. , б)
, б)  .
. ,
, 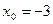 .
. .
. :
: .
. – знаком невизначеного інтеграла.
– знаком невизначеного інтеграла. . 9.
. 9.  .
. . 10.
. 10.  .
. . 11.
. 11.  .
.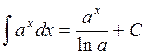 . 12.
. 12.  .
. . 13.
. 13.  .
. . 14.
. 14.  .
. . 15.
. 15.  .
. . 16.
. 16.  .
. .
. .
. .
. ,то
,то  , де и = u (x) – довільна функція, яка має неперервну похідну.
, де и = u (x) – довільна функція, яка має неперервну похідну. зробити підстановку (заміну змінної) х = φ (t), де φ (t) – це функція, яка має неперервну похідну, то
зробити підстановку (заміну змінної) х = φ (t), де φ (t) – це функція, яка має неперервну похідну, то .
. треба обов’язково повернутися до старої змінної інтегрування (підставивши замість t функцію обернену до φ (х)).
треба обов’язково повернутися до старої змінної інтегрування (підставивши замість t функцію обернену до φ (х)). .
. довільну сталу опускають. Отримані значення u, v та du підставляють в праву частину формули. Множники u і dv будуть вибрані вірно, якщо інтеграл
довільну сталу опускають. Отримані значення u, v та du підставляють в праву частину формули. Множники u і dv будуть вибрані вірно, якщо інтеграл  є простішим за інтеграл
є простішим за інтеграл  .
. ,
, 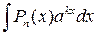 ,
, 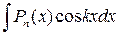 ,
,  , де Рn (х) – многочлен n -го степеня, k – число, зручно вибрати множник u = Рn (х), dv – всі інші множники.
, де Рn (х) – многочлен n -го степеня, k – число, зручно вибрати множник u = Рn (х), dv – всі інші множники. зручно взяти dv = Рn (х) dх, а u =ln(ах + b).
зручно взяти dv = Рn (х) dх, а u =ln(ах + b). ,
,  ,
,  ,
,  , де Рn (х) – многочлен, k – число, вибирають dv = Рn (х) dх, за u – функцію, що є множником при Рn (х).
, де Рn (х) – многочлен, k – число, вибирають dv = Рn (х) dх, за u – функцію, що є множником при Рn (х). і
і  можна спростити, виділивши повний квадрат в знаменнику:
можна спростити, виділивши повний квадрат в знаменнику: .
. зводить даний інтеграл до табличного.
зводить даний інтеграл до табличного. можна за допомогою підстановки
можна за допомогою підстановки  привести до інтеграла від функції, раціональної відносно t. В цьому випадку
привести до інтеграла від функції, раціональної відносно t. В цьому випадку  ,
,  ,
,  , а
, а .
. , де R – раціональна функція, можна застосувати підстановку t = sin х; в інтегралах вигляду
, де R – раціональна функція, можна застосувати підстановку t = sin х; в інтегралах вигляду  – підстановку t = cos х.
– підстановку t = cos х. , де R – раціональна функція, то він спрощується за допомогою підстановки tg x = t.
, де R – раціональна функція, то він спрощується за допомогою підстановки tg x = t. спрощується заміною змінних, яку зручно обрати в залежності від значень m і n, а саме:
спрощується заміною змінних, яку зручно обрати в залежності від значень m і n, а саме: ,
,  ;
; ,
,  ,
,  обчислюються за допомогою формул:
обчислюються за допомогою формул: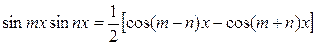 ,
, ,
, .
.
 робиться підстановка x = g (t), то формула заміни змінної має вигляд:
робиться підстановка x = g (t), то формула заміни змінної має вигляд: ,
, .
.
 .
. а
а
 б
б
 .
. .
. [ t 1; t 2], знизу – віссю О х, зліва і справа – прямими х = а, х = b, то її площа дорівнює:
[ t 1; t 2], знизу – віссю О х, зліва і справа – прямими х = а, х = b, то її площа дорівнює: ,
, .
. .
.



