
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння, що зводяться до рівнянь зі змінними, що розділяються.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема Коші Графік розв’язку диференціального рівняння називається інтегральною кривою цього рівняння. Рівняння (2) має розв’язок за таких умов: Теорема Коші(про існування і єдність розвязку) Нехай функція Ця теорема дає достатні умови існування єдиного розв’язку рівняння (2). Геометрична теорема Коші стверджує, що через кожну точку Отже, ми побачили, що рівняння (2) має безліч розв’язків. Знаходження розв’язку рівняння
Рівняння, що зводяться до рівнянь зі змінними, що розділяються. Розглянемо рівняння виду Зробимо заміну Звідси потрібно виділити Першу частину ділимо на
Із даного рівняння ми можемо знайти інтеграли, тобто
Однорідні диференціальні рівняння. Загальні поняття. Функція Наприклад: Дана функція є однорідною функцією другого виміру, тому що:
Дана функція є однорідною функцією нульового виміру, тому що:
Диференціальне рівняння
Буде однорідним тоді і тільки тоді, коли функції Нехай рівняння має вигляд:
Нехай дані функції
Робимо заміну Тепер підставляємо все це у наше рівняння:
Або це те саме, що
Скоротивши на
Згрупувавши одержане рівняння зі змінними, що розділяються:
Взявши інтеграли та замінивши
Рівняння, що зводяться до однорідних Нехай маємо рівняння виду
Розглянемо два випадки: 1) Тоді система алгебраїчних рівнянь
Має єдиний розв’язок (х0,у0). Проведемо заміну х=х1+х0 у=у1+у0, та отримаємо
Оскільки (х0,у0) є розв’язком системи алгебраїчних рівнянь, то диференціальне рівняння матиме вигляд:
І є однорідним нульового степеня. Отже, робимо заміну у1=ux1 dy1=udx1+x1du Ділимо на dx1
Домножимо на dx1, отримаємо
Об’єднуємо dx з x, du з u, отримаємо
Шукаємо інтеграл
Загальний інтеграл диференціального рівняння матиме вигляд:
2) Робимо заміну dz=a2 dx1+b2dy
Підставимо диференціальне рівняння (1) і одержимо
Звідси,
Загальний інтеграл диференціального рівняння матиме вигляд:
Лінійні диференціальні рівняння першого порядку Рівняння y ’+ p (x)⋅ y = q (x), в якому невідома функція y і її похідна y ′ входять до рівняння у першому степеню і не множаться між собою, p (x) і q (x) – неперервні на деякому проміжку функції, називається лінійним диференціальним рівнянням першого порядку. Розв'язок y (x) цього рівняння шукають у вигляді добутку двох невідомих функцій u (x) і v (x), тобто y = u ⋅ v. Тоді похідна функції приймає вигляд y ′ = u ′ v + v ′ u. Значення y (x) і y ′ підставляють у рівняння y ’+ p (x)⋅ y = q (x) і отримують вираз: u ′ v + uv ′+ p (x) uv = q (x) або u ′ v + u [ v ′+ p (x) v ]= q (x). Функцію v визначають із умови, що вираз в дужках дорівнює нулю, тобто розв'язують рівняння, яке буде завжди з відокремлюваними змінними:
Потім значення v підставляють у рівняння u ′ v = q (x) і з отриманого диференціального рівняння теж з відокремлюваними змінними знаходять загальний розв'язок u = u (x, C). Значення v і u підставляють у рівність y = u ⋅ v і визначають загаль- ний розв'язок лінійного диференціального рівняння.
Рівняння Бернуллі Рівняння виду Розділимо рівняння на уm, то одержимо
Зробимо заміну
Підставимо заміну в рівняння
Рівняння Рікатті Рівняння виду В загальному випадку рівняння Рікатті не інтегрується, відомо лише деякі частинні випадки рівняння рікатті, що інтегруються в квадратурах, розглянемо один із даних випадків.
Нехай відомий один частинний розвязок
Розкривши дужки і використовуючи вказану тотожність, одержимо
Перепишемо це рівняння наступним чином:
Отже ми отримали рівняння Бернуллі. Інтегруючий множник В деяких випадках рівняння виду
Таким чином замість звичайного диференціального рівняння відносно функції у(х) одержимо диференціальне рівняння в частинних похідних відносно функції В цьому випадку одержимо Проінтегрувавши ліву і праву частину отримаємо
Рівняння Лагранжа Рівнянням Лагранджа називають рівняння виду
Його розв’язком є рівняння
Остаточним розв’язком рівняння Лагранджа в параметричній формі записують у вигляді
Диференціальні рівняння вищих порядків, що інтегруються в квадратурах, виду: F(у(п-1), у(п))=0 Рівняння виду F(у(п-1), у(п))=0
Рівняння Клеро Частинним випадком рівняння Лагранджа Продиференціювавши дане рівняння отримаємо Можливі два випадки 1) Загальним розв’язком рівняння Клеро буде сімя прямих Теорема Коші Якщо функція Приймаємо теорему без доведень.
Теорема Коші Графік розв’язку диференціального рівняння називається інтегральною кривою цього рівняння. Рівняння (2) має розв’язок за таких умов: Теорема Коші(про існування і єдність розвязку) Нехай функція Ця теорема дає достатні умови існування єдиного розв’язку рівняння (2). Геометрична теорема Коші стверджує, що через кожну точку Отже, ми побачили, що рівняння (2) має безліч розв’язків. Знаходження розв’язку рівняння
Рівняння, що зводяться до рівнянь зі змінними, що розділяються. Розглянемо рівняння виду Зробимо заміну Звідси потрібно виділити Першу частину ділимо на
Із даного рівняння ми можемо знайти інтеграли, тобто
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.190.43 (0.011 с.) |

 і її частинна похідна
і її частинна похідна  визначені і неперервні у відкритій області G площини
визначені і неперервні у відкритій області G площини  і існує така точка з координатами
і існує така точка з координатами  , тоді існує єдиний розв’язок
, тоді існує єдиний розв’язок  рівняння (2), який задовольняє умову
рівняння (2), який задовольняє умову  при
при  , тобто
, тобто 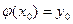 .
. і змінювати
і змінювати  не виходячи при цьому з області G, то діставатимемо різні інтегральні криві.
не виходячи при цьому з області G, то діставатимемо різні інтегральні криві.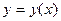 , що проходить через задану точку з координатами
, що проходить через задану точку з координатами  називається розв’язком задачі Коші.
називається розв’язком задачі Коші.

 у
у

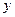
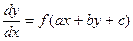 , де
, де 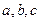 - довільні сталі.
- довільні сталі. і знайдемо похідну
і знайдемо похідну 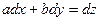 .
.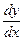 .
. :
: 
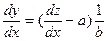 і підставимо отримане рівняння в початкове:
і підставимо отримане рівняння в початкове: .Звідси потрібно виділити
.Звідси потрібно виділити 
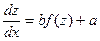
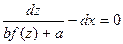

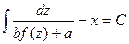 , С – певна константа Загальний інтеграл матиме вигляд
, С – певна константа Загальний інтеграл матиме вигляд
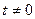 виконується тотожність
виконується тотожність  .
.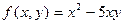
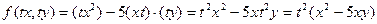


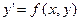 (2) називається однорідним, якщо функція
(2) називається однорідним, якщо функція 
 будуть однорідними функціями одного і того самого виміру.
будуть однорідними функціями одного і того самого виміру.


 тоді
тоді 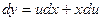 .
.

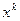 і розкривши дужки, отримаємо
і розкривши дужки, отримаємо


 отримаємо загальний інтеграл:
отримаємо загальний інтеграл: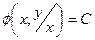

 ,
,  ,
, ,
, .
.




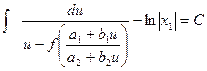

 , тобто коефіцієнти лінійно залежні і
, тобто коефіцієнти лінійно залежні і 

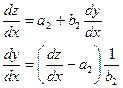
 , а це те саме, що
, а це те саме, що 







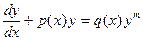 , де
, де 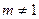 називається рівнянням Бернуллі.
називається рівнянням Бернуллі.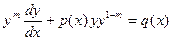



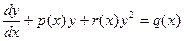 називають рівнянням Рікатті.
називають рівнянням Рікатті. , робимо заміну
, робимо заміну 
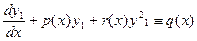


 не є рівнянням в повних диференціалах, але існує функція
не є рівнянням в повних диференціалах, але існує функція  така, що рівняння
така, що рівняння  , то рівняння буде рівнянням в повних диференціалах та достатньо умов цього є рівність; необхідно і достатньо
, то рівняння буде рівнянням в повних диференціалах та достатньо умов цього є рівність; необхідно і достатньо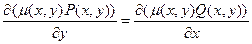
 відома функція.
відома функція.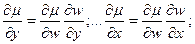 після підстановки в рівняння одержимо
після підстановки в рівняння одержимо 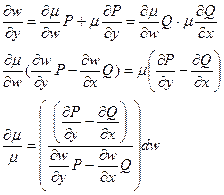
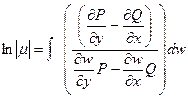
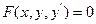 ,
, , тоді рівняння матиме вигляд
, тоді рівняння матиме вигляд  . Продефернціюємо дане рівняння
. Продефернціюємо дане рівняння  . Замінивши dy=pdx, отримаємо
. Замінивши dy=pdx, отримаємо  . Звівши ці рівняння, отримаємо
. Звівши ці рівняння, отримаємо 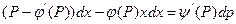 . Отже, ми отримали лінійне неоднорідне диференціальне рівняння:
. Отже, ми отримали лінійне неоднорідне диференціальне рівняння:

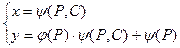
 є рівняння Клеро
є рівняння Клеро 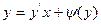 . Поклавши
. Поклавши  , отримаємо
, отримаємо 
 , оскільки
, оскільки  , підставляємо в рівняння, отримаємо
, підставляємо в рівняння, отримаємо  , отримаємо
, отримаємо  .
. 2)
2) 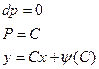
 і цю сімю огинає особлива крива
і цю сімю огинає особлива крива  та
та  .
. і її частинні похідні
і її частинні похідні  по аргументу не перервні в деякій відкритій області G, яка входить в таку область
по аргументу не перервні в деякій відкритій області G, яка входить в таку область  , то для всякої точки
, то для всякої точки 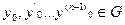 існує єдиний розв’язок у=у(х) рівняння
існує єдиний розв’язок у=у(х) рівняння  , який задовольняє початкові умови рівняння (3).
, який задовольняє початкові умови рівняння (3).


