Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні однорідні рівняння другого порядкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Зі сталими коефіцієнтами
Лінійним диференціальним рівнянням другого порядку називається рівняння
Якщо Якщо Загальний розв’язок лінійного однорідного рівняння
де
Для знаходження
Можливі наступні випадки:
Зразки розв’язування задач
Приклад 1. Розв’язати рівняння:
Розв’язання. Складемо характеристичне рівняння:
де
Приклад 2. Розв’язати рівняння:
Розв’язання. Характеристичне рівняння має вигляд
Приклад 3. Розв’язати рівняння:
Розв’язання. Маємо характеристичне рівняння
Загальний розв’язок рівняння
Приклад 4. Розв’язати задачу Коші:
Розв’язання. Характеристичне рівняння має вигляд:
Його корені
Отже, частинний розв’язок рівняння:
Приклад 5. Розв’язати задачу Коші: Розв’язання. Характеристичне рівняння
Маємо систему рівнянь
Отже, розв’язок задачі Коші матиме вигляд:
Приклад 6. Розв’язати задачу Коші:
Розв’язання. Характеристичне рівняння
Загальний розв’язок Обчислимо
Використовуючи початкові умови, знайдемо
Отже, частинний розв’язок однорідного рівняння буде
Завдання для самостійної роботи
Знайти загальні та частинні розв’язки однорідних диференціальних рівнянь другого порядку: 1) 2) 3) 4) 5) 6) 7) 8) 9) Лінійні неоднорідні диференціальні рівняння Другого порядку зі сталими коефіцієнтами із Спеціальною правою частиною
Розглянемо лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами:
Якщо права частина
де Можливі такі випадки:
1. Нехай
а) якщо
б) якщо
в) якщо Зауваження 1. Для знаходження невідомих коефіцієнтів многочлена 2. Нехай а) якщо б) якщо Зауваження 2. У цьому випадку для знаходження невідомих коефіцієнтів многочленів Якщо,
де
Зразки розв’язування задач
Приклад 1. Знайти загальний розв’язок рівняння:
Розв’язання. Загальний розв’язок рівняння має вигляд Частинний розв’язок неоднорідного рівняння залежить від вигляду правої частини Тоді
Після підстановки
Розділимо рівняння на
Прирівняємо коефіцієнти при
Тобто, Отже, загальний розв’язок лінійного неоднорідного рівняння
Приклад 2. Знайти загальний розв’язок рівняння:
Розв’язання. Загальний розв’язок цього рівняння складається з двох компонентів Враховуючи, що
Знаходимо:
Підставляючи
Розділимо обидві частини на
Прирівняємо коефіцієнти при
Тоді, Дістанемо загальний розв’язок лінійного неоднорідного рівняння у вигляді:
Приклад 3. Знайти загальний розв’язок рівняння:
Розв’язання. Аналогічно попередньому, маємо Характеристичне рівняння
Після підстановки цих виразів в початкове рівняння, дістанемо
Частинний розв’язок неоднорідного рівняння буде:
а загальний:
Приклад 4. Знайти загальний розв’язок рівняння:
Розв’язання. Маємо:
Отримаємо: Порівняємо коефіцієнти при
Дістанемо систему рівнянь:
Розв’яжемо систему рівнянь за формулами Крамера:
Отже:
Приклад 5. Знайти загальний розв’язок рівняння:
Розв’язання. Маємо:
Частинний розв’язок неоднорідного лінійного рівняння шукатимемо у вигляді
Підставимо
Після низки арифметичних перетворень останнє рівняння набуває вигляду:
Порівняємо коефіцієнти при
Отримаємо систему рівнянь
яку розв’яжемо за формулами Крамера:
Тоді
Отже, маємо Загальний розв’язок неоднорідного рівняння дістанемо у вигляді:
Приклад 6. Знайти загальний розв’язок рівняння:
Розв’язання. Загальний розв’язок відповідного однорідного рівняння
Дістанемо:
Звідки, Загальним розв’язком лінійного неоднорідного рівняння буде функція
Приклад 7. Знайти загальний розв’язок рівняння:
Розв’язання. Загальний розв’язок відповідного однорідного рівняння
відповідно. Аналогічно попередньому маємо:
Отримаємо:
Отже,
Тоді
Звідки, Загальний розв’язок початкового лінійного неоднорідного рівняння дістанемо у вигляді:
Приклад 8. Розв’язати задачу Коші:
Розв’язання. Аналогічно попередньому маємо:
Отже, загальний розв’язок однорідного рівняння буде
Підставимо
Частинний розв’язок диференціального рівняння має вигляд: Використаємо початкові умови, для цього знайдемо
Маємо:
Отже, дістанемо розв’язок задачі Коші:
Приклад 9. Розв’язати задачу Коші:
Розв’язання. Характеристичне рівняння відповідного однорідного диференціального рівняння має два рівних кореня
Маємо:
Тобто, Знайдемо
Прирівняємо коефіцієнти при
Отже: Дістанемо загальний розв’язок лінійного неоднорідного рівняння
Використаємо початкові умови, щоб знайти
Тоді:
Таким чином, розв’язок задачі Коші має вигляд:
Приклад 10. Розв’язати систему рівнянь:
Розв’язання. Систему лінійних однорідних диференціальних рівнянь першого порядку із сталими коефіцієнтами розв’яжемо зведенням її до одного диференціального рівняння другого порядку. Для цього перше рівняння системи продиференцюємо по
Замість
З останнього виразу виключимо змінну
Отже, маємо:
Тоді,
Отже, загальний розв’язок системи
Завдання для самостійної роботи
Знайти загальні частинні розв’язки задач:
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11)
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

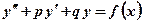 .
. та
та  є сталі числа, то рівняння називається лінійним диференціальним рівнянням другого порядку із сталими коефіцієнтами.
є сталі числа, то рівняння називається лінійним диференціальним рівнянням другого порядку із сталими коефіцієнтами. , то рівняння називається однорідним, якщо
, то рівняння називається однорідним, якщо 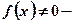 неоднорідним.
неоднорідним. має вигляд:
має вигляд: ,
,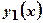 та
та  лінійно-незалежні частинні розв’язки рівняння, тобто
лінійно-незалежні частинні розв’язки рівняння, тобто  , а
, а  довільні сталі.
довільні сталі. треба розв’язати характеристичне рівняння:
треба розв’язати характеристичне рівняння: .
. корені характери-
стичного рівняння
корені характери-
стичного рівняння
 частинні розв’язки
частинні розв’язки
 ‒
загальний розв’язок
‒
загальний розв’язок




 дійсні однакові
числа
дійсні однакові
числа
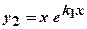
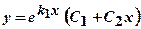
 комплексно-
комплексно-
 спряжені числа,
спряжені числа,
 уявна одиниця,
уявна одиниця,
 дійсні числа.
дійсні числа.



 .
. ,
, ,
,
 корені характеристичного рівняння дійсні та різні, тобто, загальний розв’язок рівняння має вигляд
корені характеристичного рівняння дійсні та різні, тобто, загальний розв’язок рівняння має вигляд  .
. .
. . Його корені – дійсні, рівні
. Його корені – дійсні, рівні  . Тоді загальний розв’язок рівняння має вигляд
. Тоді загальний розв’язок рівняння має вигляд  .
. .
.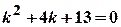 .
.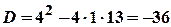 ,
, .
. .
. .
. .
. . Тоді, загальний розв’язок
. Тоді, загальний розв’язок 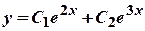 . Для того, щоб знайти частинний розв’язок треба визначити
. Для того, щоб знайти частинний розв’язок треба визначити  та
та  . Це можна зробити, використовуючи початкові умови, але спочатку треба знайти похідну
. Це можна зробити, використовуючи початкові умови, але спочатку треба знайти похідну 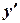 від загального розв’язку:
від загального розв’язку:  . Дістанемо систему рівнянь:
. Дістанемо систему рівнянь:
 .
.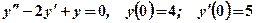 .
. . Його корені
. Його корені  . Тоді загальний розв’язок
. Тоді загальний розв’язок  . Знайдемо похідну
. Знайдемо похідну  .
.
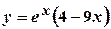 .
. .
. .
. ;
;  .
. .
.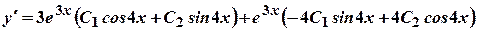 .
.
 .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. .
. лінійного неоднорідного рівняння є функцією спеціального вигляду, то рівняння можна розв’язати методом невизначених коефіцієнтів, і загальний розв’язок має вигляд:
лінійного неоднорідного рівняння є функцією спеціального вигляду, то рівняння можна розв’язати методом невизначених коефіцієнтів, і загальний розв’язок має вигляд: ,
, загальний розв’язок відповідного однорідного рівняння,
загальний розв’язок відповідного однорідного рівняння,  частинний розв’язок неоднорідного рівняння, який залежить від функції
частинний розв’язок неоднорідного рівняння, який залежить від функції  .
. , де
, де  многочлен степеня
многочлен степеня  , тобто
, тобто , тоді:
, тоді: , тоді частинний розв’язок обираємо у вигляді
, тоді частинний розв’язок обираємо у вигляді  , де
, де  многочлен ступеню
многочлен ступеню 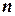 з невідомими коефіцієнтами, тобто, якщо
з невідомими коефіцієнтами, тобто, якщо
 ,
,
 ,
,
 ,
,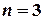
 ;
; , тоді
, тоді  ;
; , тоді
, тоді  .
. треба підставити функцію
треба підставити функцію  та її похідні першого та другого порядку в вихідне рівняння та прирівняти коефіцієнти при однакових ступенях
та її похідні першого та другого порядку в вихідне рівняння та прирівняти коефіцієнти при однакових ступенях  , де
, де  многочлени степенів
многочлени степенів  , тоді існують такі випадки:
, тоді існують такі випадки: , тоді
, тоді  , де
, де  многочлени ступеню
многочлени ступеню  з невідомими коефіцієнтами;
з невідомими коефіцієнтами;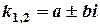 , тоді
, тоді  .
. та
та  діємо так само, але прирівнюємо коефіцієнти при
діємо так само, але прирівнюємо коефіцієнти при  , внаслідок чого знов дістанемо систему лінійних алгебраїчних рівнянь, з якої визначимо невідомі коефіцієнти.
, внаслідок чого знов дістанемо систему лінійних алгебраїчних рівнянь, з якої визначимо невідомі коефіцієнти. , де
, де  та
та  функції спеціального вигляду, то частинний розв’язок неоднорідного лінійного рівняння
функції спеціального вигляду, то частинний розв’язок неоднорідного лінійного рівняння  має вигляд
має вигляд ,
, та
та  частинні розв’язки лінійних неоднорідних рівнянь
частинні розв’язки лінійних неоднорідних рівнянь та
та  відповідно.
відповідно. .
. , де
, де  загаль-ний розв’язок відповідного однорідного рівняння
загаль-ний розв’язок відповідного однорідного рівняння  . Характеристичне рівняння
. Характеристичне рівняння  має корені
має корені  . Отже
. Отже  .
. (маємо
(маємо  ).
). . Для визначення невідомих коефіцієнтів
. Для визначення невідомих коефіцієнтів  та
та  підставимо
підставимо  в початкове рівняння. Щоб це було можливим, знайдемо першу і другу похідні від частинного розв’язку
в початкове рівняння. Щоб це було можливим, знайдемо першу і другу похідні від частинного розв’язку 
 в наше рівняння отримаємо
в наше рівняння отримаємо .
. та приведемо подібні доданки. Маємо:
та приведемо подібні доданки. Маємо: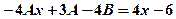 .
.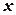 в однакових ступенях:
в однакових ступенях:
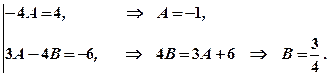
 .
. .
. .
. має вигляд
має вигляд  . Його корені:
. Його корені:  . Загальний розв’язок однорідного рівняння має вигляд:
. Загальний розв’язок однорідного рівняння має вигляд:  .
. , тобто,
, тобто,  , а також, що
, а також, що  , дістанемо частинний розв’язок неоднорідного рівняння:
, дістанемо частинний розв’язок неоднорідного рівняння: або
або  .
. ,
,

 та приведемо подібні доданки:
та приведемо подібні доданки: .
.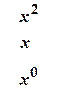

 .
. .
. .
. має однакові корені
має однакові корені  .
. , тобто,
, тобто,  . Частинний розв’язок даного неоднорідного рівняння буде мати вигляд:
. Частинний розв’язок даного неоднорідного рівняння буде мати вигляд:

 або
або
 , або
, або .
.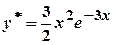 ,
, .
. .
. .
. ,
,
 .
. та
та  в обох частинах останнього рівняння:
в обох частинах останнього рівняння:

 ;
;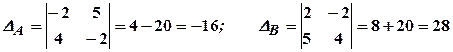 ;
; .
. , а
, а загальний розв’язок лінійного неоднорідного диференціального рівняння.
загальний розв’язок лінійного неоднорідного диференціального рівняння. .
.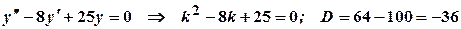 .
. , де
, де  . Загальний розв’язок однорідного рівняння
. Загальний розв’язок однорідного рівняння  .
. :
: ,
,
 ,
,
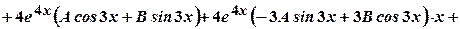


 та
та 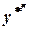 в початкове рівняння та отримаємо:
в початкове рівняння та отримаємо:
 .
. та
та 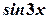 :
:







 .
. .
. .
. має вигляд
має вигляд  . Оскільки
. Оскільки  , тобто
, тобто  , то частинний розв’язок неоднорідного рівняння буде:
, то частинний розв’язок неоднорідного рівняння буде: ,
, ,
,

 . Отже
. Отже  .
. .
.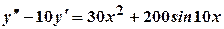 .
. має вигляд
має вигляд  . Права частина початкового рівняння складається з двох доданків:
. Права частина початкового рівняння складається з двох доданків:  , де
, де  . Тому частинний розв’язок лінійного неоднорідного рівняння теж складається з двох доданків:
. Тому частинний розв’язок лінійного неоднорідного рівняння теж складається з двох доданків:  є частинними розв’язками рівнянь:
є частинними розв’язками рівнянь: та
та 
 ,
, ,
, .
. , або
, або .
.
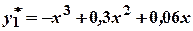 .
.
 .
.
 . Отже,
. Отже,  .
. .
. .
.
 .
.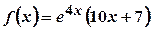 .
. ,
, ,
, .
. , або
, або .
.
 , а загальний розв’язок ‒
, а загальний розв’язок ‒  .
. .
.
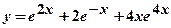 .
. .
. . Отже,
. Отже,  . Оскільки, права частина складається з суми двох різних функцій:
. Оскільки, права частина складається з суми двох різних функцій:  , то кожній з них будуть відповідати частинні розв’язки
, то кожній з них будуть відповідати частинні розв’язки  та
та  , а
, а 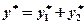 .
. ,
, ,
, .
. Розділимо це рівняння на
Розділимо це рівняння на  :
: .
.
 .
. :
:
 .
. та
та  :
:
 .
.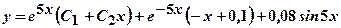 .
. та
та  , для цього треба знайти похідну від загального розв’язку:
, для цього треба знайти похідну від загального розв’язку: .
.
 .
.
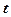 :
: .
. підставимо праву частину другого рівняння системи:
підставимо праву частину другого рівняння системи: .
. . Для цього використаємо перше рівняння системи:
. Для цього використаємо перше рівняння системи: .
. , або
, або

 .
.
 ;
; ;
;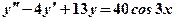 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;