
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дотичні до кривих другого порядкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо еліпс Для знаходження точок перетину прямої з еліпсом потрібно розв’язати систему трьох даних рівнянь (фактично підставити рівняння прямої у рівняння еліпса). Отримаємо:
Якщо отримане квадратне рівняння має два дійсних кореня Якщо розв’язки рівняння збігаються Отримаємо Так як корені рівняння Враховуючи, що Аналогічно міркують, отримаємо рівняння дотичних в точці з координатами та параболи:
Приклад 7. Скласти рівняння дотичних до еліпса Розв’язання: Позначимо точку дотику Так як точка У нашому випадку маємо
Оптичні властивості еліпса, гіперболи та параболи
Якщо джерело світла розмістити в одному із фокусів еліпса, то після відбиття від еліпса всі промені пройдуть через інший фокус. Якщо розмістити джерело світла у фокусі гіперболи, то після дзеркального відбиття від неї промені будуть мати такий напрямок, ніби вони виходять з іншого фокуса. Якщо ж джерело світла розмістити у фокусі параболи, то після дзеркального відбиття від неї всі промені будуть паралельними до її вісі. На цій властивості параболи ґрунтується будова прожекторів, телескопів і ін. Доведемо це. Покажемо, що дотична до параболи  Знайдемо координати точки Знайдемо координати точки  – перетину дотичної з віссю – перетину дотичної з віссю 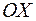 : :
Отже, Покажемо, що трикутник Рис.16 рівнобедрений. Дійсно Приклад 8. Із фокуса параболи Розв’язання: Очевидно, що фокус параболи: Знайдемо точку параболи, в якій промінь відбивається. Для цього розв’яжемо систему
Звідки Розглянемо ще один приклад на зведення загального рівняння кривої 2-го порядку до канонічного вигляду в евклідовому просторі та її побудову. Приклад 9. Привести до канонічного вигляду рівняння кривої
простору Розв’язання: Спочатку за допомогою ортогонального перетворення приведемо до канонічного вигляду квадратичну форму даної кривої: Для цього запишемо її матрицю: складемо характеристичне рівняння: і знайдемо корені цього рівняння: Отже, дана квадратична форма має канонічний вигляд
Знайдемо базисні вектори
При Нормуючи цей вектор, отримаємо:
Аналогічно знайдемо Знаючи вектори Як бачимо, це формули перетворення координат при переході до прямокутної системи координат, одержаної із старої системи за допомогою обертання навколо початку координат на кут φ =45˚. Щодо цієї нової системи крива матиме рівняння:
або Запишемо це рівняння у вигляді:
Якщо одержану вище систему координат піддати паралельному перенесенню, поклавши
то рівняння кривої прийме канонічний вигляд:
Отже, дана крива – еліпс. Підставляючи (b) в (a), одержимо формули:
переходу від початкової системи координат до тієї, в якій крива має канонічне рівняння. Щодо даної системи координат новий початок і нові базисні вектори мають координати:
Побудувавши їх, отримаємо нову систему координат
ЗАДАЧІ
1. Знайти довжини півосей та координати фокусів наступних еліпсів: а) 4х2 + 9у2 – 36 = 0; б) 4х2 + 144у2 – 576 = 0. 2. Скласти канонічне рівняння еліпса, якщо: а) вершини еліпса мають координати А1(6,0), А2(-6,0), В1(0,3), В2(0,-3); б) фокальна відстань 2с = 10, а мала піввісь b = 5; в) ексцентриситет г) ексцентриситет д) відстань між фокусами дорівнює 8, а ексцентриситет 3. Довжина великої піввісі еліпса дорівнює 6, ексцентриситет 4. Скласти рівняння еліпса в канонічній системі координат, якщо: а) еліпс проходить через точки М1 б) еліпс проходить через точки М1 (1,3), М2 (4,1); в) еліпс проходить через точку М 5. Написати рівняння директрис еліпса 6. Скласти рівняння еліпса, якщо: а) відстань між директрисами дорівнює 12, а велика піввісь дорівнює б) відстань між директрисами дорівнює в) відстань між директрисами дорівнює г) прямі х= ± 7. Знайти рівняння множини точок, для кожної з яких сума відстаней до двох точок F1(4,0) та F2(– 4,0) дорівнює 10. 8. Через фокус F1 проведена хорда еліпса 9. Хорда, що проведена через фокус F1 паралельно вісі ОY, перетинає еліпс 10. Визначити ексцентриситет еліпса, якщо його малу вісь видно з фокусів під кутом 60˚. 11. Знайти ексцентриситет еліпса, якщо відрізок між його фокусами видно з вершини малої осі під прямим кутом. 12. Знайти ексцентриситет еліпса, якщо відрізок перпендикуляра, опущеного з центра еліпса на директрису, ділиться вершиною еліпса навпіл. 13. Знайти ексцентриситет еліпса, якщо відстань між його директрисами втричі більша за відстань між фокусами. 14. Задавши на площині прямокутну систему координат, зобразити області, що визначаються наступними системами нерівностей: а) 15. Дано еліпс 16. Визначити площу чотирикутника дві вершини якого знаходяться в фокусах еліпса 17. Знайти довжини півосей та координати фокусів наступних гіпербол: а) 9х2 – 4у2 – 36 = 0; б) х2 – у2 – 5 = 0. 18. Скласти канонічне рівняння гіперболи, якщо: а) відстань між вершинами рівна 8, а відстань між фокусами –10; б) дійсна піввісь дорівнює 3 і гіпербола проходить через точку (6, 2 в) відстань між директрисами рівна г). відстань між директрисами рівна 19. Визначити піввісі, координати фокусів, ексцентриситет, рівняння асимптот та рівняння директрис наступних гіпербол: а) 4х2 – 9у2 = 36; б) 16х2 – 9у2 = 144. 20. Знайти площу S прямокутника, вершини якого лежать на гіперболі 21. Скласти канонічне рівняння гіперболи, якщо: а) гіпербола проходить через точки (4, 0) та (4 б) гіпербола проходить через точку (–5, 3) та має ексцентриситет в) гіпербола має асимптоти 4у ± х = 0 та директриси 5х ± 16=0; г) гіпербола є рівнобічною та проходить через точку ( 22. Написати рівняння гіперболи, якщо її асимптоти мають рівняння: 23. Переконавшись, що точка М( 24. Скласти канонічне рівняння гіперболи, якщо кут між асимптотами дорівнює 600 і гіпербола проходить через точку М (6,3). 25. Скласти рівняння гіперболи, що має загальні фокуси із еліпсом 26. Дана гіпербола 27. Знаючи ексцентриситет, визначити кут між асимптотами гіперболи: а) 28. Знайти площу трикутника, утвореного асимптотами гіперболи 29. Написати рівняння траєкторії руху точки М(х,у), якщо в будь-який момент часу вона знаходиться в 1,25 раз далі від точки А(5,0), ніж від прямої 5х – 16 = 0. 30. Задавши на площині прямокутну систему координат, побудувати області, що визначаються наступними системами нерівностей: а) 31. Визначити координати фокуса та скласти рівняння директриси для кожної із наступних парабол: а) у2 = 6х; б) х2 = – 4у; в) у2 = – 2х; г) х2 = 3у; д) 2х2 – 3у = 0; е) 3у2 +16х = 0. 32. Скласти канонічне рівняння параболи в кожному із наступних випадків: а) відстань від фокуса, що лежить на осі ОX, до вершини дорівнює 4; б) парабола симетрична відносно осі абсцис та проходить через точку М(1,2); в) парабола симетрична відносно осі ординат та проходить через точку М(5,1). 33. Скласти канонічне рівняння параболи в кожному з наступних випадків: а) фокус має координати (3,0); б) фокус має координати (0,5); в) директриса має рівняння х + 15 = 0; г) директриса має рівняння у + 12 = 0. 34. Обчислити фокальний радіус FM точки М параболи у2 = 8х, якщо її абсциса дорівнює 8. 35. Знайти фокальний радіус точки М параболи 36. На параболі 37. На параболі х2 = – 12у знайти точку, фокальний радіус якої рівний 9. 38. Визначити площу трикутника, у якого одна вершина належить директрисі параболи у2=2рх, а дві інші є кінцями хорди, яка проходить через фокус перпендикулярно до осі ОX. 39. Скласти рівняння траєкторії руху точки М (х,у), якщо в будь-який момент часу вона є рівновіддаленою від точки А(8, 4) та вісі ординат. 40. Обчислити довжини півосей та відстань між фокусами еліпса, заданого в полярній системі координат рівнянням а). 41. Дано еліпси: а) Написати рівняння цих еліпсів у полярній системі координат, полюс якої знаходиться в одному з фокусів еліпса, а полярна вісь направлена у сторону іншого фокуса. 42. В кожному із наступних випадків скласти канонічне рівняння параболи, що задана у полярній системі координат: а) 43. Написати рівняння парабол: а) у2 = 2х; б) у2 = 10х у полярній системі координат, якщо полюс співпадає із фокусом параболи, а полярна вісь – із віссю ОX. 44. Побудувати криві: а) г) 45. Побудувати криві: 1) х2 + 2х + у2 –3 = 0; 2) х2 – х + у2 – 3) х2 – у2 – 4 = 0; 4) х2 – у2 – х – у – 5) х2 + 2х – у2 – 8 = 0; 6) у2 + 2у – х + 1 = 0; 7) х2 – 4у + 4 = 0; 8) х2 – 6у2 – 12х +36у – 48 = 0. 46. Знайти центр, піввісі, ексцентриситет і рівняння директрис еліпса: 5х2 + 9у2 – 30х + 18у + 9 = 0. 47. Знайти центр, піввісі, ексцентриситет, рівняння директрис і асимптот гіперболи: а) 16х2 – 9у2 – 64х – 54у = 0; б) 9х2 – 16у2 + 90х + 32у – 367 = 0. 48. Знайти координати вершини і рівняння директриси параболи: а) у2 = 4х – 8; б) у2 = 4 – 6х; в) х2 = 2 – у; г) у = 4х2 – 8х + 7.
За допомогою повороту прямокутної системи координат привести до канонічного вигляду наступні рівняння кривих другого порядку. Написати формули перетворення і зобразити дані криві: 49 50. 51. 52. 53. 54.
За допомогою повороту прямокутної системи координат і переносу початку привести до канонічного вигляду наступні рівняння кривих. Написати формули перетворення координат і побудувати дані криві: 55. 56. 57. 58. 59.
Розділ 4 Поверхні другого порядку Поверхні обертання
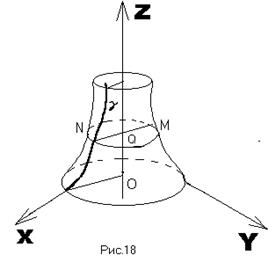
Поверхня, яка разом з будь-якою своєю точкою містить все коло, отримане обертанням цієї точки навколо деякої фіксованої прямої, називається поверхнею обертання (рис. 18). Пряма, навколо якої виконується обертання, називається віссю обертання. Якщо поверхню обертання перетинати площинами, перпендикулярними до вісі обертання, то отримаємо кола. Такі кола називаються паралелями поверхні. Площини, які проходять через вісь обертання, перетинають поверхню обертання по лініях, які називаються меридіанами. Нехай в прямокутній системі координат (
Отже, щоб отримати рівняння поверхні обертання, утвореної обертанням лінії Аналогічно можна отримати поверхні обертання навколо інших координатних осей. Еліпсоїд Еліпсоїдом називається поверхня, яка в деякій прямокутній системі координат визначається рівнянням:
Величини a, b, c називаються півосями еліпсоїда. Дослідимо форму еліпсоїда і побудуємо його: 1. Так як x, y, z, входять в рівняння (22) тільки в парних степенях, то еліпсоїд симетричний відносно координатних площин, осей і початку координат. Центр симетрії еліпсоїда називається центром еліпсоїда, а вісі симетрії – його осями. Точки перетину еліпсоїда з осями координат: А1(а,0,0); А2(-а,0,0); В1(0,b,0); В2(0,-b,0); С1(0,0,с); С2(0,0,-с) називаються вершинами еліпсоїда. 2. Із рівняння (1) маємо: 3. Розглянемо перерізи еліпсоїда координатними площинами і площинами, паралельними до них. Площина XOY і паралельні до неї площини мають рівняння z=h. В перетині еліпсоїда з такими площинами отримаємо Можливі три випадки: 1). ú h ÷ < c, тоді маємо 2). ú h ÷ = c, то одержуємо 3). ÷ h ÷ > c, то одержуємо рівняння уявного еліпса, отже в цьому випадку площина z=h з еліпсоїдом не має спільних точок. Повністю аналогічно розглядаються перерізи еліпсоїда площинами x=h і y=h. Побудувавши еліпси в координатних площинах, отримаємо зображення еліпсоїда (рис.19). Відмітимо, що якщо в рівнянні (22) а,b,с – різні, то еліпсоїд називається трьохвісним, а якщо які-небудь дві із півосей рівні, наприклад а=с, то в перетині з площинами y=h, де ú h ÷ < b, отримаємо кола (рис.20). В цьому випадку еліпсоїд можна одержати обертанням еліпса § 26. Конус Конусом 2-го порядку називається поверхня, яка в деякій прямокутній системі координат визначається рівнянням:
Покажемо, що конус складається із прямих, які проходять через початок системи координат. Нехай точка М0(x0,y0,z0) – довільна точка конуса (23), відмінна від точки О(0,0,0). Тоді координати точки М0 задовольняють рівняння конуса отже, Так як змінні x,y,z входять в рівняння конуса лише в парних степенях, то він симетричний відносно координатних площин, осей і початку координат. Дослідимо форму конуса (23) методом перерізів і побудуємо його. 1). Розглянемо перерізи конуса площиною XOY і паралельними до неї площинами. Їх рівняння z=h. В перетині отримаємо:
а) якщо h=0, то одержимо точку О(0,0,0), b) якщо h ¹ 0, то фігура перетину – еліпс (рис. 21). Таким чином, конус, який має рівняння (23) – це множина всіх прямих простору, які проходять через точку О і точки будь-якого еліпса з центром в точці Q, яка належить вісі OZ (Q ¹ О). У цьому випадку еліпс називається направляючим, а вісь OZ називається віссю конуса. Відмітимо, що направляючою конуса називається довільна лінія розміщена на ньому і для якої виконується умова, що будь-яка прямолінійна твірна перетинає її в одній і тільки одній точці. 2). Розглянемо перерізи конуса площиною XOZ і паралельними до неї площинами. Їх рівняння y=k. В перетині отримаємо:
a) в площині XOZ, тобто коли k=0, маємо пару прямих, які перетинаються в точці О(0,0,0) (рис.21), b) якщо k¹0 то отримаємо гіперболу з дійсною віссю паралельною до OZ. 3). Аналогічні до другого випадку перерізи отримаємо і в площині YOZ та паралельних до неї площинах: x=m.
Переріз конуса з площиною, яка не проходить через точку О може бути як еліпсом, гіперболою, так і параболою (переріз площиною, яка паралельна деякій твірній). Таким чином криві другого порядку (еліпс, гіперболу, параболу) можна розглядати як перерізи конуса другого порядку площинами. Тому їх часто називають конічними перерізами. § 27. Однопорожнинний гіперболоїд Однопорожнинним гіперболоїдом називається поверхня, яка в деякій прямокутній системі координат визначається рівнянням: Додатні числа a,b,c називаються півосями однопорожнинного гіперболоїда. Оскільки змінні входять в рівняння (24) тільки в парних степенях, то однопорожнинний гіперболоїд симетричний відносно всіх координатних площин, осей і початку системи координат. Дві вісі OX і OY перетинають однопорожнинний гіперболоїд. Вони називаються дійсними, а вісь OZ не перетинає його, тому називається уявною. Точки перетину поверхні з координатними осями називаються вершинами. Дослідимо форму однопорожнинного гіперболоїда методом перерізів і побудуємо його. 1). Розглянемо перерізи однопорожнинного гіперболоїда площиною YOZ і паралельними до неї площинами. Їх рівняння x=k. В перетині отримаємо:
Можливі три випадки: а) якщо ÷ k ÷ < a то маємо гіперболу з асимптотами b) якщо ÷ k ÷ = a – одержуємо пару прямих, що перетинаються, c) якщо ÷ k ÷ > a – одержуємо гіперболу з дійсною віссю, яка паралельна до вісі OZ). Якщо k=0 – одержуємо гіперболу в площині YOZ, яку і будуємо (дивись рис. 22). 2). Повністю аналогічні до попереднього перерізи отримуються в перетині однопорожнинного гіперболоїда площиною XOZ і паралельними до неї площинами: y=m. 3). Розглянемо перерізи однопорожнинного гіперболоїда площиною XOY і паралельними до неї площинами. В перетині отримаємо:
Якщо h=0, то одержуємо, горловий еліпс: Якщо a=b, то отримаємо рівняння у вигляді: Всі асимптоти однопорожнинного гіперболоїда проходять через точку О і задовольняють рівняння:
§ 28. Двопорожнинний гіперболоїд
Двопорожнинним гіперболоїдом називається поверхня, яка в деякій прямокутній системі координат має рівняння:
Додатні числа a,b,c називаються півосями двопорожнинного гіперболоїда. Оскільки змінні x,y,z входять в рівняння (25) тільки в парних степенях, то двопорожнинний гіперболоїд симетричний відносно всіх координатних площин, осей і початку системи координат. Вісі OX і OY не перетинають двопорожнинний гіперболоїд. Вони називаються уявними, а вісь OZ перетинає його в точках Дослідимо форму двопорожнинного гіперболоїда методом перерізів і побудуємо його. 1). Розглянемо перерізи двопорожнинного гіперболоїда площиною XOY і паралельними до неї площинами:
Можливі три випадки: a). Якщо÷ h ÷ < c то в перетині – порожня множина. b). Якщо÷ h ÷ = c то отримаємо c). Якщо÷ h ÷ > c т
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 4684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.011 с.) |

 і пряму
і пряму 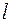 задану параметричними рівняннями:
задану параметричними рівняннями:  .
. або
або
 то отримаємо дві точки перетину прямої і еліпса.
то отримаємо дві точки перетину прямої і еліпса. то пряма
то пряма  . Підставивши це значення параметра в рівняння прямої
. Підставивши це значення параметра в рівняння прямої 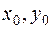 точки дотику. Оскільки ця точка належить еліпсу, то її координати задовольняють рівняння еліпса:
точки дотику. Оскільки ця точка належить еліпсу, то її координати задовольняють рівняння еліпса:  .
.
 і
і 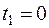 , то і
, то і  . Це можливо лише тоді, коли
. Це можливо лише тоді, коли 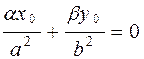 . Знайшовши з рівнянь прямої
. Знайшовши з рівнянь прямої  ,
,  і підставивши в останню рівність, отримаємо рівняння
і підставивши в останню рівність, отримаємо рівняння  .
. (18)
(18) (19)
(19) . (20)
. (20) , перпендикулярних до прямої
, перпендикулярних до прямої  .
. . Нормальний вектор даної прямої буде направляючим для дотичної отже,
. Нормальний вектор даної прямої буде направляючим для дотичної отже,  , або
, або  .
. належить еліпсу, то
належить еліпсу, то  , крім того для дотичної
, крім того для дотичної  .
. . Розв’язавши систему
. Розв’язавши систему , отримаємо два розв’язки:
, отримаємо два розв’язки:  ,
,  і
і ,
,  , отримаємо рівняння дотичних:
, отримаємо рівняння дотичних:  і
і  .
. утворює рівні кути з фокальним радіусом
утворює рівні кути з фокальним радіусом  і прямою
і прямою  , де
, де  проекція точки
проекція точки  на директрису (рис. 16)
на директрису (рис. 16) , або
, або .
. .
.
 і
і  отже, і кути
отже, і кути  . Але
. Але  як внутрішні різносторонні кути при паралельних прямих, тому і
як внутрішні різносторонні кути при паралельних прямих, тому і 
 , що і потрібно було довести.
, що і потрібно було довести. під кутом 450 до осі
під кутом 450 до осі  . Знайдемо рівняння прямої, якій належить промінь світла, що виходить з фокуса. Скористаємося рівнянням прямої з кутовим коефіцієнтом:
. Знайдемо рівняння прямої, якій належить промінь світла, що виходить з фокуса. Скористаємося рівнянням прямої з кутовим коефіцієнтом:  . Оскільки
. Оскільки  , то
, то  .
. . Знайшовши з першого рівняння
. Знайшовши з першого рівняння  і підставивши в друге отримаємо:
і підставивши в друге отримаємо: або
або  .
. і
і 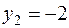 . За умовою задачі нам потрібен додатній корінь точка перетину променя (а не всієї прямої) з параболою, тому рівняння шуканої прямої
. За умовою задачі нам потрібен додатній корінь точка перетину променя (а не всієї прямої) з параболою, тому рівняння шуканої прямої  .
.
 за допомогою переходу до нової прямокутної системи координат. Вказати вид кривої. Побудувати її.
за допомогою переходу до нової прямокутної системи координат. Вказати вид кривої. Побудувати її. (див. § 13).
(див. § 13). ,
, 

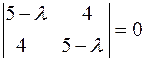
 ,
,  .
. .
. і
і  нової прямокутної системи координат. Вони є власними векторами лінійного оператора, що має ту ж матрицю, що і дана квадратична форма; отже, їх координати задовольняють системі рівнянь:
нової прямокутної системи координат. Вони є власними векторами лінійного оператора, що має ту ж матрицю, що і дана квадратична форма; отже, їх координати задовольняють системі рівнянь:
 одержимо систему, еквівалентну рівнянню
одержимо систему, еквівалентну рівнянню  . Один з розв’язків цього рівняння
. Один з розв’язків цього рівняння  . Вектор
. Вектор 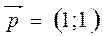 – власний вектор, який відповідає значенню
– власний вектор, який відповідає значенню  .
.
 – власний вектор, який відповідає значенню
– власний вектор, який відповідає значенню  , і вектор
, і вектор 
 і
і  , запишемо формули ортогонального перетворення, яке приводить дану квадратичну форму до канонічного вигляду:
, запишемо формули ортогонального перетворення, яке приводить дану квадратичну форму до канонічного вигляду:  (а)
(а)




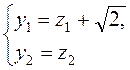 (b),
(b),



 ,
, 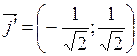 .
. розташування якої відносно даної прямокутної системи координат
розташування якої відносно даної прямокутної системи координат  та зображення еліпса показано на рисунку 17.
та зображення еліпса показано на рисунку 17. , велика піввісь а = 3;
, велика піввісь а = 3; , а мала піввісь b = 2;
, а мала піввісь b = 2; .
. , а відстань від точки М еліпса до фокуса F1 дорівнює 7. Знайти відстань від точки М до фокуса F2 та координати точки М. Написати канонічне рівняння еліпса.
, а відстань від точки М еліпса до фокуса F1 дорівнює 7. Знайти відстань від точки М до фокуса F2 та координати точки М. Написати канонічне рівняння еліпса. та М2 (-3, 0);
та М2 (-3, 0); та має ексцентриситет
та має ексцентриситет  .
. та знайти відстань між ними.
та знайти відстань між ними. ;
; , а між фокусами
, а між фокусами  ;
; , а ексцентриситет
, а ексцентриситет  ;
; є директрисами еліпса, а мала піввісь дорівнює 2.
є директрисами еліпса, а мала піввісь дорівнює 2. , паралельна канонічній вісі ОY. Визначити довжину цієї хорди.
, паралельна канонічній вісі ОY. Визначити довжину цієї хорди. в точках М1 та М2. Визначити відстань від точок М1 та М2 до фокуса F2.
в точках М1 та М2. Визначити відстань від точок М1 та М2 до фокуса F2. б)
б) 
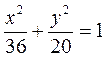 . Знайти фокальні радіуси точок М1(3,
. Знайти фокальні радіуси точок М1(3,  ) та М2(-2,
) та М2(-2,  ), що належать даному еліпсу.
), що належать даному еліпсу. , а дві інші співпадають з кінцями малої осі.
, а дві інші співпадають з кінцями малої осі. );
);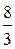 а ексцентриситет
а ексцентриситет  .
. , а відстань між фокусами = 26
, а відстань між фокусами = 26 , а дві сторони проходять через фокуси паралельно до вісі ОY. Обчислити S для випадку, коли а2 = 20 та b2 = 10.
, а дві сторони проходять через фокуси паралельно до вісі ОY. Обчислити S для випадку, коли а2 = 20 та b2 = 10. , 4);
, 4); ;
; , 1).
, 1).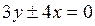 а відстань між фокусами рівна 20
а відстань між фокусами рівна 20 ) належить гіперболі
) належить гіперболі 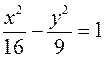 , знайти її фокальні радіуси.
, знайти її фокальні радіуси.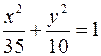 та проходить через точку М(4
та проходить через точку М(4  , 3).
, 3).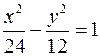 . Написати рівняння спряженої з нею гіперболи; знайти ексцентриситети, директриси та асимптоти даної та спряженої гіперболи.
. Написати рівняння спряженої з нею гіперболи; знайти ексцентриситети, директриси та асимптоти даної та спряженої гіперболи. ; б)
; б)  .
. і прямої перпендикулярної до дійсної вісі і проведеної через фокус.
і прямої перпендикулярної до дійсної вісі і проведеної через фокус. б)
б) 
 , якщо ордината точки М рівна 6.
, якщо ордината точки М рівна 6. знайти точку, фокальний радіус якої рівний 13.
знайти точку, фокальний радіус якої рівний 13. ; б).
; б).  .
. ; б)
; б) 
 ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. = 0;
= 0;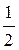 = 0;
= 0; .
. .
.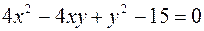 .
. .
. .
.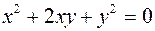 .
.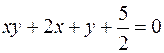 .
. .
. .
. .
. .
.
 ) задана лінія
) задана лінія  , яка лежить в площині
, яка лежить в площині 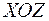 . Тоді вона має рівняння
. Тоді вона має рівняння  . Знайдемо рівняння поверхні, яка утвориться при обертанні лінії
. Знайдемо рівняння поверхні, яка утвориться при обертанні лінії  навколо осі
навколо осі  . Візьмемо на поверхні довільну точку
. Візьмемо на поверхні довільну точку  і проведемо через неї площину, перпендикулярну до осі
і проведемо через неї площину, перпендикулярну до осі  , радіуса
, радіуса  . З іншого боку, цей радіус є абсцисою точки
. З іншого боку, цей радіус є абсцисою точки  лінії
лінії  , апліката якої
, апліката якої  . Підставивши в рівняння лінії
. Підставивши в рівняння лінії 
 , отримаємо рівняння поверхні обертання навколо осі
, отримаємо рівняння поверхні обертання навколо осі  , або
, або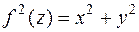 (21)
(21) , що лежить в площині
, що лежить в площині  .
. (22)
(22) . Аналогічно для y і z:
. Аналогічно для y і z:  і
і  Отже, всі точки еліпсоїда лежать всередині прямокутного паралелепіпеда із сторонами 2а, 2b, 2с (крім вершин), з центром в точці О.
Отже, всі точки еліпсоїда лежать всередині прямокутного паралелепіпеда із сторонами 2а, 2b, 2с (крім вершин), з центром в точці О.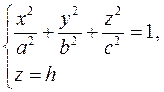 або
або  .
. – еліпс. При зменшенні ú h ÷ піввісі його збільшуються і коли h=0, одержуємо еліпс
– еліпс. При зменшенні ú h ÷ піввісі його збільшуються і коли h=0, одержуємо еліпс 
 – дві уявні прямі, що перетинаються в дійсних точках С1(0,0,с); С2(0,0,-с).
– дві уявні прямі, що перетинаються в дійсних точках С1(0,0,с); С2(0,0,-с).
 (23)
(23) . Розглянемо точку М(tx0,ty0,tz0), де tÎ R. Точка М також належить конусу, оскільки
. Розглянемо точку М(tx0,ty0,tz0), де tÎ R. Точка М також належить конусу, оскільки 
 . Таким чином разом з точкою М0 конусу належить вся пряма, яка проходить через початок координат і має направляючий вектор
. Таким чином разом з точкою М0 конусу належить вся пряма, яка проходить через початок координат і має направляючий вектор  . Отже, конус можна розглядати як множину деяких прямих, які проходять через точку О, які називаються твірними. Точка О називається вершиною конуса.
. Отже, конус можна розглядати як множину деяких прямих, які проходять через точку О, які називаються твірними. Точка О називається вершиною конуса. або
або  . Можливі випадки:
. Можливі випадки: або
або 
 Якщо в рівнянні (23) a=b, то конус називається конусом обертання, або круговим конусом.
Якщо в рівнянні (23) a=b, то конус називається конусом обертання, або круговим конусом. (24)
(24) .
. (з дійсною віссю, яка паралельна до осі OY),
(з дійсною віссю, яка паралельна до осі OY),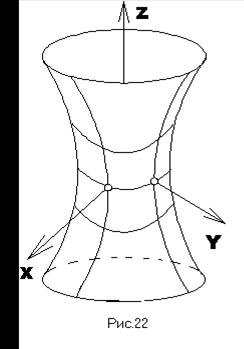
 - еліпс.
- еліпс. . При зростанні ÷ h ÷ піввісі еліпса необмежено збільшуються разом із еліпсом. побудуємо горловий еліпс, та пару еліпсів в площинах паралельних до XOY (на однаковій відстані до неї) (рис.22).
. При зростанні ÷ h ÷ піввісі еліпса необмежено збільшуються разом із еліпсом. побудуємо горловий еліпс, та пару еліпсів в площинах паралельних до XOY (на однаковій відстані до неї) (рис.22). . Це однопорожнинний гіперболоїд обертання. Його можна отримати обертанням гіперболи:
. Це однопорожнинний гіперболоїд обертання. Його можна отримати обертанням гіперболи: 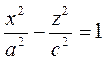 навколо вісі OZ.
навколо вісі OZ.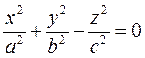 , тобто належать конусу, який називається асимптотичним конусом однопорожнинного гіперболоїда.
, тобто належать конусу, який називається асимптотичним конусом однопорожнинного гіперболоїда. (25)
(25) . які називаються вершинами. Вісь OZ називається дійсною.
. які називаються вершинами. Вісь OZ називається дійсною. .
.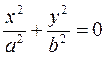 , тобто маємо точки
, тобто маємо точки 


