
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гомотетія як приклад перетворення подібності. Властивості гомотетіїСодержание книги
Поиск на нашем сайте
Перетворення площини називається перетворенням подібності (подібністю), якщо існує число
Якщо Тобто рух – це частковий випадок перетворення подібності. Розглянемо приклад перетворення подібності, відмінного від руху. Зафіксуємо точку Кожній точці М площини поставимо у відповідність точку
Покажемо, що гомотетія є перетворенням подібності. Розглянемо ще одну точку N площини та її образ – точку
Таким чином гомотетія є перетворенням подібності з коефіцієнтом k= · якщо · якщо · якщо
Нехай точка М має координати x, y, а точка
Розглянемо властивості гомотетії. 1. Гомотетія з коефіцієнтом Доведення. Нехай пряма l в деякій системі координат має рівняння: 2. Гомотетія зберігає просте відношення трьох точок. Доведення. Нехай при гомотетії точки Розглянемо їх прості відношення
Але, згідно рівності (3)
3. Гомотетія переводить відрізок у відрізок, промінь у промінь, півплощину в півплощину. Доведення випливає з перших двох властивостей. 4. Гомотетія переводить кут у рівний йому кут.
Нехай АВС даний кут, а А'В'С ' – його образ. За формулою (3) отримаємо: 5. Гомотетія зберігає орієнтацію площини. Доведення. Розглянемо репер R=(B,A,C) і його образ при гомотетії Отже, гомотетія має такі ж властивості як і рухи першого роду. Аналітичне задання подібності. Властивості подібності Покажемо, що послідовне виконання двох перетворень подібності (їх композиція) є перетворенням подібності. Розглянемо два перетворення подібності f з коефіцієнтом подібності k1 і g з коефіцієнтом k2 та довільні дві точки А і В площини. Тоді:
Таким чином композиція двох перетворень подібності з коефіцієнтами k1 і k2 буде перетворенням подібності з коефіцієнтом Теорема 3. Якщо f – перетворення подібності з коефіцієнтом Доведення. Покажемо, що такий рух існує. Розглянемо перетворення
Покажемо, що такий рух єдиний. Припустимо, що існує ще один рух
Отже, ми довели, що перетворення подібності – це композиція гомотетії і руху. Так як гомотетія має такі ж властивості як і рух, то з урахуванням теореми і подібність має властивості: 1. Подібність переводить пряму в пряму, паралельні прямі в паралельні прямі. 2. Подібність зберігає просте відношення трьох точок. 3. При перетворенні подібності кут переходить в рівний йому кут. 4. При подібності півплощина переходить у півплощину. 5. Подібність змінює орієнтацію площини, якщо рух змінює орієнтацію площини (рух невласний) і не змінює в противному (якщо рух власний). В першому випадку перетворення подібності називається невласним (перетворенням подібності 2-го роду), в другому – власним (перетворенням подібності 1-го роду). Нехай аналітичне задання подібності Скористаємося теоремою 3. Розглянемо гомотетію h з центром в точці О і коефіцієнтом k. Її аналітичне задання Нехай g – рух, який задовольняє рівність (5). Аналітичне задання руху Отже, якщо точка М(x,y) при перетворенні подібності перейде в точку
Теорема 4. Будь-яке перетворення подібності, відмінне від руху, має тільки одну нерухому точку. Доведення. Нехай перетворення подібності має аналітичне задання (7). Точка М(х,у) буде нерухомою точкою цього перетворення тільки тоді, коли Розглянемо визначник C цієї системи:
Якщо ε=1, то C=1–k2. Отже, при Наслідок. Перетворення подібності, яке не має нерухомих точок, або має більше ніж одну нерухому точку є рухом.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.009 с.) |

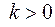 таке, що для будь-яких точок А і В і їх образів
таке, що для будь-яких точок А і В і їх образів  і
і  виконується умова
виконується умова .
.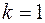 , то отримаємо рух площини.
, то отримаємо рух площини. і число
і число 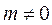 .
.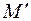 таку, щоб виконувалась рівність:
таку, щоб виконувалась рівність: 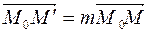 (2) (рис.5).
(2) (рис.5).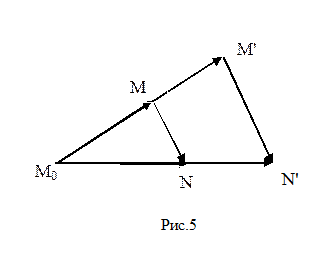 Таке перетворення площини називається гомотетією з центром в точці
Таке перетворення площини називається гомотетією з центром в точці 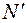 (рис.5). Тоді
(рис.5). Тоді  .
. 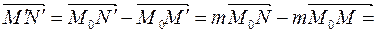
 Отже,
Отже, (3)
(3)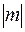 .
. , то маємо тотожне перетворення,
, то маємо тотожне перетворення,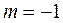 , то це перетворення – центральна симетрія відносно точки
, то це перетворення – центральна симетрія відносно точки 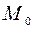 ,
,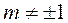 , то гомотетія відмінна від руху.
, то гомотетія відмінна від руху.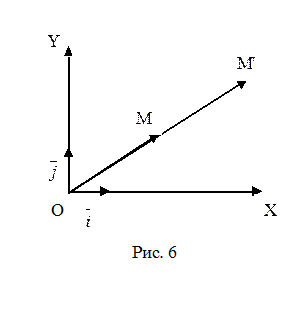 Задамо на площині систему координат
Задамо на площині систему координат  , і розглянемо точку М та її образ точку
, і розглянемо точку М та її образ точку  при гомотетії з центром в точці О(0,0) (рис.6). Одержимо аналітичне задання такої гомотетії.
при гомотетії з центром в точці О(0,0) (рис.6). Одержимо аналітичне задання такої гомотетії.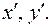 Тоді за означенням гомотетії
Тоді за означенням гомотетії 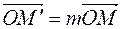 . Перейшовши до координат, отримаємо:
. Перейшовши до координат, отримаємо: (4)
(4)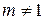 переводить пряму, яка не проходить через центр гомотетії в паралельну їй пряму, а пряму яка проходить через центр гомотетії –в себе.
переводить пряму, яка не проходить через центр гомотетії в паралельну їй пряму, а пряму яка проходить через центр гомотетії –в себе.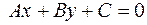 . Для знаходження рівняння її образа
. Для знаходження рівняння її образа  використаємо формули (4). З них отримаємо:
використаємо формули (4). З них отримаємо:  і підставивши в рівняння прямої l одержимо рівняння
і підставивши в рівняння прямої l одержимо рівняння  . Отже,
. Отже, 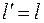 , якщо С=0 (пряма l проходить через початок координат).
, якщо С=0 (пряма l проходить через початок координат).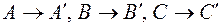 .
.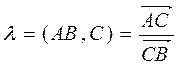 і
і 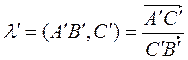 , або
, або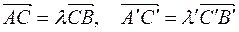 .
.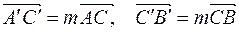 . Отже,
. Отже,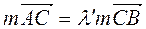 , або
, або 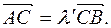 Таким чином
Таким чином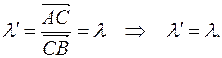
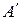 Доведення.
Доведення.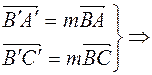
 .
.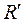 =
= 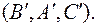 Так як
Так як  , а
, а  , то R і
, то R і 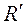 однаково орієнтовані, тобто гомотетія зберігає орієнтацію площини.
однаково орієнтовані, тобто гомотетія зберігає орієнтацію площини.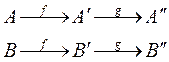 . За означенням подібності
. За означенням подібності  Отже,
Отже,  .
.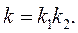
 , а h – гомотетія з цим же коефіцієнтом
, а h – гомотетія з цим же коефіцієнтом 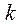 і з центром в точці
і з центром в точці 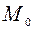 , то існує єдиний рух
, то існує єдиний рух 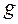 , такий що
, такий що 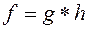 . (5)
. (5)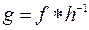 (6)
(6)  , тобто є рухом. Помножимо обидві частини рівності (6) на h справа:
, тобто є рухом. Помножимо обидві частини рівності (6) на h справа: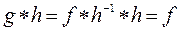 . Отже,
. Отже, 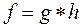 і існування руху g доведено.
і існування руху g доведено.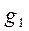 , такий, що
, такий, що 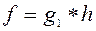 . Помножимо обидві частини цієї рівності на
. Помножимо обидві частини цієї рівності на 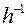 :
: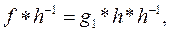 або
або 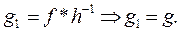
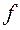 перетворення подібності з коефіцієнтом k. Задамо на площині деяку систему координат
перетворення подібності з коефіцієнтом k. Задамо на площині деяку систему координат 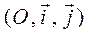 і отримаємо в ній
і отримаємо в ній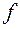 .
.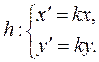

 , то аналітичне задання подібності матиме вигляд:
, то аналітичне задання подібності матиме вигляд: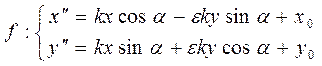 (7)
(7)
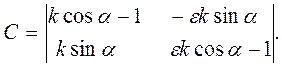
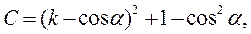 а якщо ε= -1, то
а якщо ε= -1, то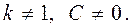 Таким чином система має єдиний розв’язок – єдину нерухому точку перетворення.
Таким чином система має єдиний розв’язок – єдину нерухому точку перетворення.


