
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рухи площини. Властивості рухівСодержание книги
Поиск на нашем сайте
Перетворення площини зберігає відстані, якщо відстань між будь-якими двома точками А і В площини рівна відстані між їхніми образами А¢ і В¢, тобто Перетворення площини, яке зберігає відстані, називається рухом. Найбільш простим прикладом руху є тотожне перетворення площини, тобто перетворення, при якому кожна точка площини переходить в себе. Приведемо ще один приклад руху.
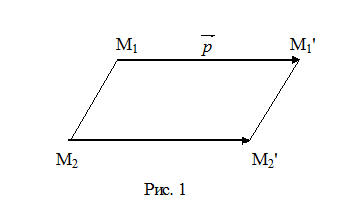
Доведемо, що паралельне перенесення є рухом. Нехай М1 і М2 - дві точки площини (рис. 1), а М1¢ і М2¢ – їх образи. Потрібно показати, що За означенням паралельного перенесення: Отже, паралельне перенесення – рух площини. Впорядковану трійку точок A, B, C площини, які не лежать на одній прямій називають репером. Позначають: Точку A називають початком, а B і C – вершинами.
Якщо Фактично репер – це система координат, де А – початок, а В і С кінці базисних векторів. Очевидно, що при рухові репер переходить в репер, причому ортонормований репер переходить в ортонормований репер (так як Теорема 2. Нехай Доведення. Доведемо спочатку, що такий рух існує. Задамо відображення При цьому відображенні маємо:
Таке відображення Покажемо, що
Покажемо, що Припустимо, що існує ще один рух
Так як
Аналогічно
Таким чином точки Зупинимося на властивостях руху. 1. Рух переводить пряму у пряму, причому паралельні прямі в паралельні прямі. Доведення. Розглянемо ортонормований репер Очевидно, що пряма 2. Рух зберігає просте відношення трьох точок.
Нагадаємо, що простим відношенням трьох точок, які лежать на одній прямій Нехай в репері R три довільні точки А, В, С прямої мають координати: Тоді координати точки С обчислюються за формулами:
Нехай репер Як наслідок, середина відрізка переходить в середину відрізка. З попереднього легко отримати: 3. Рух зберігає поняття „лежати між”. 4.Рух переводить півплощину з границею l в півплощину з границею 5. Рух переводить промінь в промінь. 6. Рух переводить кут в рівний йому кут (так як переводить трикутник в рівний йому трикутник). Отже, перпендикулярні прямі при русі переходять в перпендикулярні прямі.
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.21.70 (0.009 с.) |

 .
. Розглянемо на площині
Розглянемо на площині  вектор
вектор  . Кожній точці М площини
. Кожній точці М площини 
 =
=  , то паралельне перенесення – тотожне перетворення.
, то паралельне перенесення – тотожне перетворення.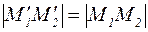 .
. – паралелограм, тому
– паралелограм, тому  .
.
 Якщо
Якщо  – довільний, то репер називається афінним (рис.2).
– довільний, то репер називається афінним (рис.2). , і
, і 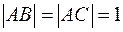 , то репер називають ортонормованим.
, то репер називають ортонормованим.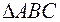 переходить у рівний йому трикутник
переходить у рівний йому трикутник  ).
).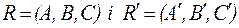 два довільні ортонормовані репери площини. Тоді існує єдиний рух, який переводить
два довільні ортонормовані репери площини. Тоді існує єдиний рух, який переводить  , причому будь-яка точка М з даними координатами в репері
, причому будь-яка точка М з даними координатами в репері  переходить в точку
переходить в точку 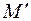 з такими ж координатами в репері
з такими ж координатами в репері  .
. так щоб будь-якій точці М в репері R відповідала точка
так щоб будь-якій точці М в репері R відповідала точка 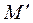 з такими ж координатами в репері
з такими ж координатами в репері  :
:  .
. ,
, ,
, .
.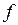 буде взаємно-однозначним, тобто є перетворенням площини.
буде взаємно-однозначним, тобто є перетворенням площини. зберігає відстані між точками, тобто є рухом. Розглянемо точки
зберігає відстані між точками, тобто є рухом. Розглянемо точки  і
і  . Тоді
. Тоді ,
,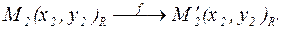 ,
, і
і  . Отже,
. Отже,  , тобто
, тобто  є рухом.
є рухом.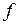 єдиний рух площини, який переводить
єдиний рух площини, який переводить  і зберігає координати точок.
і зберігає координати точок.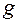 такий, що задовольняє умову теореми. Але тоді на площині існує така точка М, що її образ
такий, що задовольняє умову теореми. Але тоді на площині існує така точка М, що її образ  при рухові f не співпадає з її образом
при рухові f не співпадає з її образом  при рухові g.
при рухові g.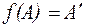 , і
, і  , то
, то , тобто точка
, тобто точка 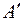 рівновіддалена від точок
рівновіддалена від точок 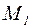 і
і  .
. ,
,  і
і , отже точка
, отже точка  рівновіддалена від точок
рівновіддалена від точок  ,
,  , то
, то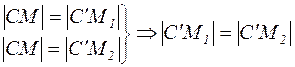 , отже, точка
, отже, точка 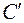 рівновіддалена від точок
рівновіддалена від точок  , отже, вони лежать на одній прямій, чого бути не може, так як (
, отже, вони лежать на одній прямій, чого бути не може, так як (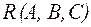 і його образ після руху
і його образ після руху  . Нехай пряма l в репері R має рівняння
. Нехай пряма l в репері R має рівняння  . Тоді, згідно теореми 2, образ
. Тоді, згідно теореми 2, образ  цієї прямої в репері
цієї прямої в репері  визначається таким же рівнянням (як множина образів всіх точок прямої l) отже, є прямою.
визначається таким же рівнянням (як множина образів всіх точок прямої l) отже, є прямою. в репері R має рівняння
в репері R має рівняння  . При рухові вона перейде в пряму
. При рухові вона перейде в пряму 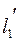 з таким же рівнянням в репері
з таким же рівнянням в репері  .
. Доведення.
Доведення.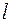 (рис.3) називають таке число
(рис.3) називають таке число 
 ,
,  ,
,  .
.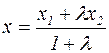 ,
,  .
. – образ репера
– образ репера  при русі. Тоді точки
при русі. Тоді точки  .
.


