
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Будь-які дві прямолінійні твірні різних сімейств належать одній площині.Содержание книги
Поиск на нашем сайте
Зауважимо, що, крім розглянутих сімей прямолінійних твірних є ще дві прямолінійні твірні однопорожнинного гіперболоїда, які лежать у площинах, паралельних до площини XOZ. Це такі прямі:
Ці прямі відповідають значенням α=¥ і β=¥. Вони разом із сімействами (31) і (32) визначають усі прямолінійні твірні однопорожнинного гіперболоїда. Властивість однопорожнинного гіперболоїда (складатися з прямолінійних твірних) використовується на практиці – побудова башт, радіо і телещогл і ін. Ідея такого використання належить російському інженерові В.Г.Шухову (1853-1939р.), який запропонував конструкцію з металевих балок, розміщених так, як прямолінійні твірні однопорожнинного гіперболоїда обертання. Такі конструкції виявилися дуже міцними і легкими, що й зумовило їх широке використання в будівництві. Гіперболічний параболоїд має рівняння: Записавши це рівняння так: гіперболічного параболоїда:
Вони мають такі ж властивості, як і прямолінійні твірні однопорожнинного гіперболоїда. Крім того, легко бачити, що всі твірні з сімейства (33) паралельні до площини
§ 33. Дотична площина до поверхні другого порядку
Еліпсоїд і гіперболоїди можна задати рівнянням Розглянемо пряму
Якщо отримане квадратне рівняння має два дійсних кореня Якщо ж розв’язки збігаються Виберемо на поверхні деяку точку Покажемо, що геометричне місце дотичних до поверхні в заданій точці P являє собою площину. Так як точка Оскільки Так як З рівнянь прямої знаходимо: Очевидно, що отримане рівняння є рівнянням площини, яка називається дотичною площиною до поверхні в точці Оскільки точка P належить поверхні, то Отже, рівняння дотичних площин до еліпсоїда і гіперболоїдів матимуть вигляд:
Аналогічно отримують рівняння дотичних площин до параболоїдів в точці
ЗАДАЧІ
1. Скласти рівняння поверхні, утвореної обертанням прямої, заданим рівняннями 2. Скласти рівняння поверхні, утвореної обертанням параболи, заданої системою рівнянь: 3. Скласти рівняння поверхні, утвореної обертанням параболи 4. У площині YOZ дано коло з центром в точці (0, 4, 0) радіуса r=1. Написати рівняння поверхні, утвореної обертанням даного кола навколо осі ОZ. 5. Коло радіуса r розташоване на площині YOZ так, що дотикається осі ОZ в початку координат. Написати рівняння поверхні, утвореної обертанням даного кола навколо осі ОZ. 6. Парабола з параметром 7. Скласти рівняння поверхні, утвореної обертанням навколо осі ОY кожної з наступних кривих, розташованих на площині XOY: а) еліпса в) гіперболи 8. Написати рівняння поверхні, утвореної обертанням синусоїди 9. Знайти радіус кола, по якому площина, 10. Визначити вид поверхні другого порядку, заданої рівнянням 11. Знайти піввісі і вершини еліпса, по якому площина 12. Дослідити методом перерізів наступні поверхні другого порядку, задані в прямокутній системі координат рівняннями: а) б) 13. Написати рівняння еліпсоїда, осі якого співпадають з осями координат і який: а) проходить через точку М (2, 0, 1) і перетинає площину XOY по еліпсу б) проходить через точку в) перетинає площину YOZ по еліпсу 14. Написати рівняння еліпсоїда, який проходить через точки (2, 2, 4), (0, 0, 6), (2, 4, 2), і для якого координатні площини даної прямокутної системи координат є площинами симетрії. 15. Скласти рівняння циліндричної поверхні твірні якої паралельні до осі OZ, а направляюча визначається системою рівнянь: 16. Скласти рівняння кругової циліндричної поверхні, якщо а) віссю служить вісь OX, а радіус направляючого кола рівний а; б) віссю служить вісь OY, і точка 17. Зобразити циліндричні поверхні, задані рівнянням а) 18. Визначити вид поверхні другого порядку, заданої рівнянням 19. Визначити перетин однопорожнинного гіперболоїда 20. Написати канонічне рівняння однопорожнинного гіперболоїда, якщо він: а) проходить через точку б) перетинає площину XOY по колу 21. Написати рівняння двопорожнинного гіперболоїда в канонічній системі координат, якщо точки 22. Знайти множину точок, для кожної з яких модуль різниці відстаней від двох даних точок (0, 0, 3), (0, 0, –3) є величина постійна, рівна 4. 23. Знайти вершину і фокальний параметр параболи, по якій площина 24. Дослідити методом перерізів наступні поверхні другого порядку, задані в прямокутній системі координат рівняннями. Побудувати їх зображення. а) в) д) 25. Визначити вид поверхні другого порядку, заданої рівнянням. Дослідити її методом перерізів. Побудувати її зображення в прямокутній системі координат. а) в) д) є) 26. Дослідити методом перерізів наступні поверхні другого порядку, задані в прямокутній декартовій системі координат. Побудувати їх зображення. а) б) в) г) д) е) 27. Написати рівняння двох систем прямолінійних твірних однопорожнинного гіперболоїда 28. На гіперболічному параболоїді 29. Знайти ті прямолінійні твірні однопорожнинного гіперболоїда Індивідуальне домашнє завдання:
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.179.30 (0.006 с.) |

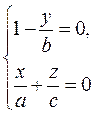 і
і 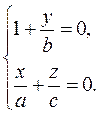
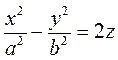 .
.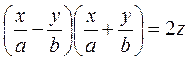 , отримаємо дві системи рівнянь, які визначають дві сім’ї прямолінійних твірних
, отримаємо дві системи рівнянь, які визначають дві сім’ї прямолінійних твірних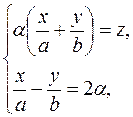 (33) і
(33) і 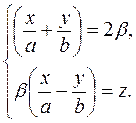 (34)
(34) , а з сімейства (34) паралельні до площини
, а з сімейства (34) паралельні до площини 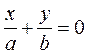 .
.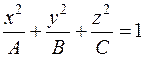 , де
, де 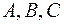 – не від’ємні одночасно.
– не від’ємні одночасно.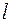 задану параметричними рівняннями:
задану параметричними рівняннями: 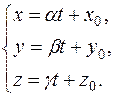 Знайдемо точки перетину прямої
Знайдемо точки перетину прямої 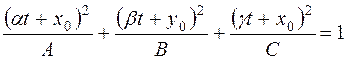 , або
, або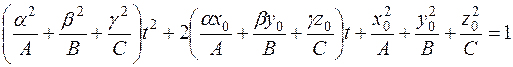 .
.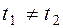 , то це параметри точок перетину прямої і поверхні. Підставивши їх в рівняння прямої, отримаємо координати точок перетину.
, то це параметри точок перетину прямої і поверхні. Підставивши їх в рівняння прямої, отримаємо координати точок перетину.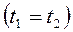 , то пряма
, то пряма 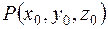 . Дотична до будь-якої лінії на поверхні, яка проходить через точку P, називається дотичною до поверхні в цій точці.
. Дотична до будь-якої лінії на поверхні, яка проходить через точку P, називається дотичною до поверхні в цій точці.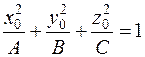 і маємо рівняння:
і маємо рівняння: 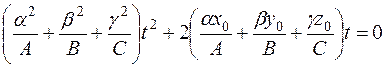 .
.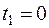 , то і
, то і  , що можливо лише у випадку, коли
, що можливо лише у випадку, коли 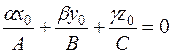 .
.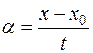 ,
,  ,
, 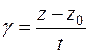 і підставивши ці значення в останню рівність, отримаємо геометричне місце дотичних до поверхні:
і підставивши ці значення в останню рівність, отримаємо геометричне місце дотичних до поверхні: 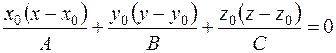 .
.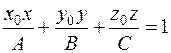 .
. (еліпсоїда),
(еліпсоїда),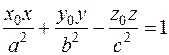 (однопорожнинного гіперболоїда),
(однопорожнинного гіперболоїда),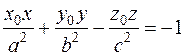 (двопорожнинного гіперболоїда).
(двопорожнинного гіперболоїда). (еліптичного параболоїда),
(еліптичного параболоїда), (гіперболічного параболоїда).
(гіперболічного параболоїда). навколо осі OZ. Вказати вид цієї поверхні, побудувати її зображення.
навколо осі OZ. Вказати вид цієї поверхні, побудувати її зображення.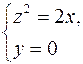 навколо осі OZ.
навколо осі OZ.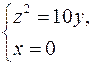 навколо осі OZ.
навколо осі OZ.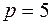 розташована на площині YOZ так, що директриса співпадає з віссю ОZ. Написати рівняння поверхні, утвореної обертанням даної параболи навколо осі ОZ.
розташована на площині YOZ так, що директриса співпадає з віссю ОZ. Написати рівняння поверхні, утвореної обертанням даної параболи навколо осі ОZ.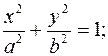 б) гіперболи
б) гіперболи 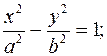
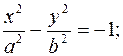 г) параболи
г) параболи 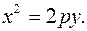
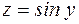 навколо осі OZ.
навколо осі OZ.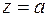 перетинає сферу
перетинає сферу 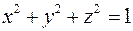 .
.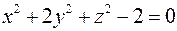 . Побудувати її зображення.
. Побудувати її зображення.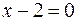 перетинає еліпсоїд
перетинає еліпсоїд 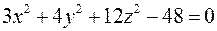 .
.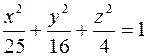 ;
;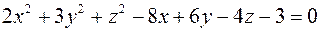 .
.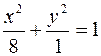 ;
;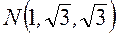 і перетинає площину YOZ по еліпсу
і перетинає площину YOZ по еліпсу 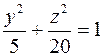 ;
; , а площину XOY по колу
, а площину XOY по колу 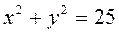 .
.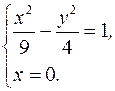
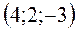 належить поверхні.
належить поверхні. ; б)
; б) 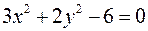 .
. . Побудувати її зображення.
. Побудувати її зображення.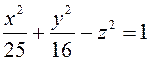 з площиною, проведеною через точку (0, 0, 1) паралельно до площини XOY.
з площиною, проведеною через точку (0, 0, 1) паралельно до площини XOY. і перетинає площину XOZ по гіперболі
і перетинає площину XOZ по гіперболі 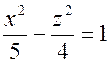 ;
;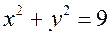 , а площину XOZ по гіперболі
, а площину XOZ по гіперболі 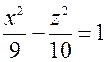 .
.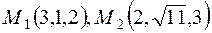 і
і 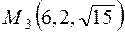 належать даній поверхні.
належать даній поверхні.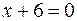 перетинає параболоїд
перетинає параболоїд  .
. ; б)
; б) 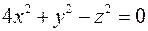 ;
;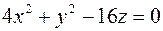 ; г)
; г) 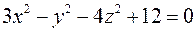 ;
;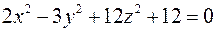 ; е)
; е)  ;
;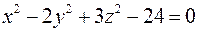 ; б)
; б) 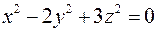 ;
;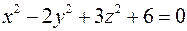 ; г)
; г) 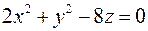 ;
; ; е)
; е) 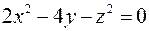 ;
; ; ж)
; ж) 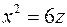 .
.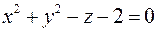 .
.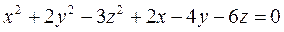 ;
;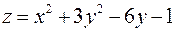 ;
;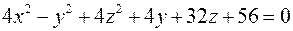 .
. ;
;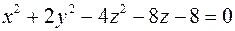 .
. і визначити ті із них, які проходять через точку A
і визначити ті із них, які проходять через точку A 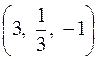 .
.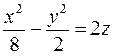 знайти прямолінійні твірні, які паралельні до площини
знайти прямолінійні твірні, які паралельні до площини 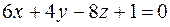 .
.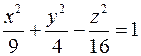 , які перпендикулярні до осі OY.
, які перпендикулярні до осі OY.


