
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класифікація перетворень подібностіСодержание книги
Поиск на нашем сайте
Класифікацію перетворень подібності проведемо в залежності від існування інваріантних точок і прямих. Будемо розглядати перетворення подібності відмінне від руху. Власні перетворення подібності. Нехай перетворення подібності 1) g – тотожне перетворення. В цьому випадку 2) g – центральна симетрія. Тоді 3) g – поворот на кут Отже, власне перетворення подібності, відмінне від руху гомотетія, або центрально-подібний поворот. Невласні перетворення подібності. Згідно теореми 4 перетворення подібності Отже, існує три типи перетворення подібності, відмінного від руху: 1) Гомотетія. 2) Центрально-подібний переворот. 3) Центрально-подібна симетрія.
Група подібності та її підгрупи
Позначимо Р – множину всіх перетворень подібності. Покажемо, що Р – група. Згідно теореми 1, потрібно перевірити дві умови: замкненість і існування оберненого елемента. Замкненість ми уже довели (див §7). Там ми показали, що композиція двох перетворень подібності буде подібністю (навіть вказали її коефіцієнт подібності Очевидно, що для будь-якого перетворення подібності Називається вона групою подібностей. Так як будь-який рух є частковим випадком перетворення подібності (подібність з коефіцієнтом k=1), то група рухів є підгрупою групи подібностей. Ясно що всі підгрупи групи рухів (див §5) будуть в свою чергу підгрупами і групи подібностей. Розглянемо приклади інших підгруп групи Р. Нехай P1 – множина всіх власних перетворень подібності. Замкненість операції на цій множині очевидна (композиція двох власних перетворень подібності буде власним перетворенням подібності). Існування оберненого до будь-якого власного перетворення подібності також очевидне. Отже, P1 - група власних перетворень подібності, підгрупа групи Р. Позначимо Р(М0) множину всіх гомотетій з центром в точці М0. Неважко перевірити, що Р(М0) – група, підгрупа групи Р.
Афінні перетворення Перетворення площини називається афінним, якщо воно довільні три точки Очевидно, що будь-яке перетворення подібності і будь-який рух являються афінними перетвореннями (оскільки вони зберігають просте відношення трьох точок). Лема 1. Якщо афінні перетворення Доведення. Нехай М – довільна точка прямої АВ, відмінна від А і В, а Так як Теорема 5. Нехай R=(A,B,C) і Доведення. Покажемо спочатку, що таке афінне перетворення Покажемо що Нехай Їх образи в репері Отже,
Доведемо єдиність перетворення f. Припустимо, що f1 - ще одне афінне перетворення, яке задовольняє умову теореми. Нехай М – довільна точка площини, а
Згідно леми Тому Наслідок. Якщо точки Очевидно (як і для рухів), що будь-яке афінне перетворення або зберігає, або змінює орієнтацію площини (репери R і
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.36.215 (0.006 с.) |

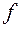 з коефіцієнтом k має тільки одну нерухому точку, позначимо її О. Позначимо h - гомотетію з центром О і коефіцієнтом k. За теоремою 3 існує такий рух g, що
з коефіцієнтом k має тільки одну нерухому точку, позначимо її О. Позначимо h - гомотетію з центром О і коефіцієнтом k. За теоремою 3 існує такий рух g, що 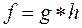 . Оскільки
. Оскільки  і h власні перетворення подібності то і рух g – власний причому
і h власні перетворення подібності то і рух g – власний причому  . Таким чином
. Таким чином  – поворот навколо точки О. Можливі три випадки:
– поворот навколо точки О. Можливі три випадки: =
=  , отже,
, отже, 
 .
. ,
,  і
і  . В цьому випадку
. В цьому випадку  - композиція гомотетії і повороту. Вона називається центрально-подібним поворотом.
- композиція гомотетії і повороту. Вона називається центрально-подібним поворотом. з коефіцієнтом k має єдину нерухому точку О (
з коефіцієнтом k має єдину нерухому точку О ( ). За теоремою 3
). За теоремою 3  ).
). з коефіцієнтом
з коефіцієнтом  . Отже, множина Р всіх перетворень подібності утворює групу. Операція тут – послідовне виконання двох перетворень подібності (їх композиція).
. Отже, множина Р всіх перетворень подібності утворює групу. Операція тут – послідовне виконання двох перетворень подібності (їх композиція). які лежать на одній прямій переводить в точки
які лежать на одній прямій переводить в точки  , які належать одній прямій і зберігає їх просте відношення, тобто (
, які належать одній прямій і зберігає їх просте відношення, тобто ( )=(
)=( )
) і
і  переводять дві точки А і В відповідно в точки
переводять дві точки А і В відповідно в точки  і
і  , то
, то  , де М довільна точка прямої АВ.
, де М довільна точка прямої АВ. .
. і
і  – афінні перетворення, то
– афінні перетворення, то  і
і  , тому
, тому 
 і
і  співпадають, тобто
співпадають, тобто  .
. – довільні репери площини. Тоді існує єдине афінне перетворення f, яке переводить репер R в
– довільні репери площини. Тоді існує єдине афінне перетворення f, яке переводить репер R в  . При цьому будь-яка точка М з даними координатами в репері R переходить в точку
. При цьому будь-яка точка М з даними координатами в репері R переходить в точку  з тими ж координатами в репері
з тими ж координатами в репері  .
. . Відображення
. Відображення  – афінне перетворення.
– афінне перетворення. – три довільні точки однієї прямої, які в репері R мають координати:
– три довільні точки однієї прямої, які в репері R мають координати:  ,
, 
 .
. мають такі ж координати:
мають такі ж координати: 
 ,
,  .
. , оскільки в обох випадках ми маємо одні і ті ж формули ділення відрізка у відношенні
, оскільки в обох випадках ми маємо одні і ті ж формули ділення відрізка у відношенні  :
: ,
,  . Тому f – афінне перетворення.
. Тому f – афінне перетворення.
 Через точку М проведемо пряму так, щоб вона перетинала будь-які дві із прямих АВ, ВС або АС в різних точках N і Р (рис.7)
Через точку М проведемо пряму так, щоб вона перетинала будь-які дві із прямих АВ, ВС або АС в різних точках N і Р (рис.7) ,
, 
 отже,
отже,  і
і  співпадають.
співпадають. , які не належать одній прямій, являють собою нерухомі точки афінного перетворення
, які не належать одній прямій, являють собою нерухомі точки афінного перетворення  – тотожне перетворення.
– тотожне перетворення.
 однаково або протилежно орієнтовані). Отримаємо афінні перетворення 1-го і 2-го роду.
однаково або протилежно орієнтовані). Отримаємо афінні перетворення 1-го і 2-го роду.


