
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхні другого порядку та їх класифікація.Содержание книги
Поиск на нашем сайте Аналогом кривих другого порядку являються в просторі поверхні другого порядку. Поверхнею другого порядку називається множина всіх точок простору, координати яких в деякій афінній системі координат задовольняють рівняння (8): a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a14x+2a24y+2a34z+a44=0, де коефіцієнти а11, а22, а33, а12, а13, а23 не рівні нулю одночасно. Міркуючи аналогічно, як і у випадку кривих, ми за теоремою 6, а потім, згрупувавши однакові змінні і виділивши повні квадрати, одержимо канонічне рівняння поверхні другого порядку: l1x2+l2y2+l3z2+Q=0, де Q – многочлен не вище першої степені. Розглянувши всі можливі випадки, які можна отримати з цього рівняння (аналогічно із кривими), одержимо класифікацію поверхонь другого порядку:
Теорема 8. Існує 17 типів поверхонь другого порядку.
Зведення квадратичної форми до канонічного вигляду в евклідовому векторному просторі Для зведення квадратичної форми до канонічного вигляду в евклідовому просторі можна скористатися, наприклад, методом ортогональних перетворень, який детально розглядається в лінійній алгебрі. Суть його в тому, що симетричну матрицю можна звести до діагонального вигляду за допомогою деякого ортогонального перетворення (тобто переходу від однієї прямокутної системи координат до іншої прямокутної системи координат). Причому діагональними елементами отриманої матриці будуть різні корені характеристичного рівняння даної матриці, а нові базисні вектори знаходимо нормувавши власні вектори, що відповідають характеристичним кореням. Зупинимося на цьому методі більш детально. Розглянемо квадратичну форму від трьох змінних: F(x,y,z)=a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz. Щоб привести квадратичну форму до канонічного вигляду і знайти формули перетворення систем координат, потрібно: 1. Скласти матрицю квадратичної форми F(x,y,z) А= та розв’язати її характеристичне рівняння
2. Записати канонічний вигляд квадратичної форми F(x¢,y¢,z¢)=l1x¢ 2+l2y¢ 2+l3z¢ 2. 3. Знайти власні вектори лінійного оператора, що має ту ж матрицю, що і дана квадратична форма. Їм відповідають характеристичні корені λ1, λ2, λ3 . 4. Пронормувавши власні вектори, отримаємо базис 5. Знаючи координати нових базисних векторів, записуємо формули перетворення прямокутних систем координат (див. [12, § 17]). Ми розглянули випадок, коли характеристичні корені λ1, λ2, λ3 різні. Що робити, коли серед характеристичних коренів є однакові, покажемо на прикладі 17. Приклад 2. За допомогою ортогонального перетворення евклідового векторного простору Розв’язання: Запишемо матрицю квадратичної форми:
Обчисливши визначника, одержимо:
Звідки отримаємо: Отже, квадратична форма має канонічний вигляд:
Залишається отримати формули перетворення. Визначимо ортонормований базис Нові базисні вектори є власними векторами лінійного оператора, що має ту ж матрицю, що і дана квадратична форма; отже, їх координати задовольняють системі рівнянь:
Знайдемо вектор
Знайдемо який-небудь з розв’язків одержаної системи. Вважаючи, наприклад,
Для знаходження другого базисного вектора
Як і вище, знайдемо: Нарешті, при Отже, формули перетворення мають вигляд:
Якщо підставити ці значення Приклад 3. За допомогою ортогонального перетворення евклідового векторного простору Розв’язання: Аналогічно до попереднього приклада складаємо характеристичне рівняння
його корені: Шуканим канонічним виглядом даної квадратичної форми є форма Знайдемо базис, в якому дана квадратична форма має канонічний вигляд. Відмінність цієї задачі від попередньої полягає у тому, що тепер характеристичне рівняння має кратний корінь 5. Цьому кореню відповідають два вектори Запишемо для даної квадратичної форми систему:
При
Один з розв’язків цього рівняння виберемо довільно. Прийнявши, наприклад,
Потім знайдемо вектор
З цієї системи знаходимо, що
Щоб знайти вектор Одним з розв’язків цієї системи є:
Запишемо формули ортогонального перетворення, яке приводить дану квадратичну форму до канонічного вигляду: Оскільки при знаходженні вектора
ЗАДАЧІ
За допомогою заміни базису афінного простору знайти канонічний вигляд квадратичної форми і записати формули перетворення координат. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
Привести квадратичну форму до канонічного вигляду: 15. 16. 17. 18. 19. 20. 21. 22.
За допомогою ортогонального перетворення евклідового векторного простору 23. 24. 25. 26.
Привести до канонічного вигляду рівняння кривої за допомогою переходу до нової прямокутної системи координат. Вияснити вид кривої і знайти формули перетворення координат у просторі 27. 28. 29. 30. 31.
Привести до канонічного вигляду рівняння поверхні за допомогою переходу до нової прямокутної системи координат. Вказати вид поверхні і знайти формули перетворення координат у просторі 32. 33. 34. 35. 36. 37.
Розділ 3 Криві другого порядку Еліпс Еліпсом називається множина всіх точок площини координати яких, в деякій прямокутній системі координат, задовольняють рівняння: де а ³ b>0. Якщо а=b, то маємо коло. Еліпс можна отримати з кола стисканням до вісі OX. З рівняння еліпса маємо: Так як змінні в рівняння еліпса входять лише в другій степені, то еліпс симетричний відносно координатних осей і початку системи координат. Точки A1, A2, B1, B2, в яких еліпс перетинає вісі системи координат, називаються вершинами еліпса. Відмітимо елементи еліпса, які не залежать від орієнтації координатних осей: 1. (2а –велика вісь), 2. число b – мала піввіс ь (2b – мала вісь), 3. 2c – фокальна відстань (c2=a2-b2), 4. e = 5. точка О(0,0) – центр еліпса, 6. А1(а,0), А2(-а,0), В1(0,b), В2(0,-b) – вершини еліпса, 7. Точки F1(с,0), F2(-с,0) називаються фокусами, 8. прямі d1 i d2, які мають рівняння: x= Розглянемо довільну точку М, яка належить еліпсу. Відрізки, які сполучають її з фокусами називаються фокальними радіусами точки М (довжини цих відрізків також називають фокальними радіусами точки М). Нехай точка М еліпса має координати x, y. Тоді ÷ MF2 ÷ = = Аналогічно міркуючи, отримаємо: ÷ MF1 ÷ =÷ -ex+a ÷. Так як для всіх точок еліпса ex < a,то модулі приймають лише додатні значення, тому: ÷ MF1 ÷= -ex+a, ÷ MF2 ÷ = ex+a. Тоді÷ MF1 ÷ + ÷ MF2 ÷ =2a. Отже, ми отримали геометричне означення еліпса:
Параметричні рівняння еліпса. Нехай задано еліпс канонічним рівнянням: Побудуємо в прямокутній системі Проведемо промінь ОК. Нехай він утворює з віссю ОХ кут φ. Точки перетину променя з колами позначимо N i Q. Проведемо через точку N пряму паралельну до oсі OX, а через Q пряму паралельну до OY. В перетині цих прямих отримаємо точку M(x, y). Тоді x=a cos φ, y=b sin φ. Покажемо, що точка M(acos φ, bsin φ) належить еліпсу. Дійсно, її координати задовольняють рівняння: Таким чином ми отримали параметричні рівняння еліпса:
y=b sin φ, де φ – параметр (0 Приклад 4. У прямокутній системі координат дана точка А(1,0) та пряма х = 2. Скласти рівняння лінії, кожна точка М(х,у) якої вдвічі ближче до точки А, ніж до даної прямої; Розв’язання: За умовою 2МА=MN (рис. 10).
Рис. 10
Таким чином шукана лінія – еліпс. Точка А співпадає з його правим фокусом, а пряма х = 2 являється його правою директрисою; Приклад 5. Привести до канонічного вигляду рівняння кривої 4х2 + 9у2 + 32х – 54у + 109 = 0 та побудувати її. Розв’язання: Доповнимо члени, що містять х, та члени, що містять у, до повних квадратів. Отримаємо:
тобто маємо еліпс, центр якого знаходиться у точці С(– 4, 3), велика піввісь якого а = 3, а мала піввісь b = 2 (рис.11). Рис.11
Гіпербола. Гіперболою називається множина всіх точок площини координати яких, в деякій прямокутній системі координат, задовольняють рівняння: З рівняння гіперболи маємо:
Отже, між прямими x = a і x = – a немає точок гіперболи. Так як в рівняння гіперболи входять тільки змінні парної степені, то гіпербола симетрична відносно осей OX, OY і початку системи координат. Ясно, що інших осей симетрії гіпербола не має, так як будь-яка вісь її симетрії проходить через точку О, а значить являється і віссю симетрії кола x2+y2=a2, яке має з гіперболою дві спільні точки А1(а,0) та А2(-а,0); тому будь-яка вісь симетрії переводить А1 в А2 і навпаки, або залишає їх нерухомими. А це лише прямі OX і OY. При побудові гіперболи досить побудувати її у першій координатній четверті, а в інших – по симетрії. З рівняння гіперболи маємо: Таким чином, гіперболу можна побудувати за допомогою прямокутника із сторонами 2a і 2b, його діагоналі будуть асимптотами (рис.12). Основні елементи гіперболи, які не залежать від орієнтації системи координат: 1. а – дійсна піввісь; 2а – дійсна вісь. 2. b – уявна піввісь; 2b – уявна вісь. 3. 2c – фокальна відстань (c2=a2+b2). 4. 5. Точки А1(а,0) та А2(-а,0) – вершини гіперболи. 6. Точка О(0,0) – центр гіперболи. 7. Точки F1(c,0) і F2(-c,0) – фокуси гіперболи. 8. Прямі d1 і d2: 9. Прямі Відрізки, які сполучають довільну точку гіперболи з фокусами, називаються фокальними радіусами. Як і для еліпса знайдемо:÷ MF1 ÷ = ÷ ex – a ÷, ÷ MF2 ÷ = ÷ ex + a ÷ Але так як для гіперболи ÷ ex ÷ > ÷ x ÷ >a то
÷ MF1 ÷ –÷ MF2 ÷ = Одержали геометричне означення гіперболи: гіперболою називається множина всіх точок площини, модуль різниці відстаней від яких, до двох даних точок F1 і F2 (фокусів) є величина постійна (рівна 2а). Відмітимо, що у випадку a=b гіпербола називається рівносторонньою. Теорема 9. Якщо за вісі прямокутної системи координат взяти асимптоти рівносторонньої гіперболи, то в цій системі координат гіпербола являє собою графік оберненої пропорційності Доведення. Розглянемо рівносторонню гіперболу задану рівнянням x2 – y2=a2 впрямокутній системі координат (O, Підставивши у рівняння гіперболи x2 – y2=a2, отримаємо:
Звідки: Теорему доведено. Якщо
§ 19. Парабола.
Параболою називається множина всіх точок площини, координати яких, в деякій прямокутній системі координат задовольняють рівняння: Так як у рівнянні параболи в парній степені лише ордината, то парабола симетрична тільки відносно вісі OX і розміщена в першій і четвертій чвертях, якщо р>0 (рис.13) і другій та третій, якщо р<0. Вісь симетрії параболи називається віссю параболи. Парабола проходить через точку О(0,0), яка називається вершиною параболи. Інших точок перетину з осями координат парабола не має, тому вісь OX – єдина вісь симетрії параболи. Нехай р>0, тоді якщо x®¥ тоі y®¥ (рис.13).
1. число р – фокальний параметр. 2. число 3. точка F( 4. пряма d: Теорема 10. Парабола – це множина тих і тільки тих точок площини, які рівновіддалені від фокуса і директриси. Доведення. Нехай точка M(x,y) рівновіддалена від F і d. Умова рівновіддаленості:
Звідки Навпаки, нехай точка М належить параболі, яка має рівняння Знайдемо відстань від точки М до фокуса:
Приклад 6.
Розв’язання: За умовою задачі МА = MN (рис.14). Звідси, Рис. 14
Отримали рівняння параболи. Точка А співпадає з її фокусом, пряма х = 2 її директриса (рис. 14).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 889; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.018 с.) |


















 , де аij=aji,
, де аij=aji, (так як матриця А симетрична, то отримаємо три дійсних кореня: λ1, λ2, λ3).
(так як матриця А симетрична, то отримаємо три дійсних кореня: λ1, λ2, λ3). в якому квадратична форма має канонічний вигляд.
в якому квадратична форма має канонічний вигляд.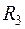 привести до канонічного вигляду квадратичну форму
привести до канонічного вигляду квадратичну форму  і знайти формули відповідного перетворення.
і знайти формули відповідного перетворення. і складемо характеристичне рівняння:
і складемо характеристичне рівняння: .
. або
або  і
і .
. .
. .
. (*)
(*) , який відповідає власному значенню
, який відповідає власному значенню 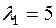 . Для цього в системі рівнянь (*) покладемо
. Для цього в системі рівнянь (*) покладемо  . Отримаємо:
. Отримаємо: .
. одержимо, що
одержимо, що  . Вектор
. Вектор  – один з власних векторів, який відповідає значенню
– один з власних векторів, який відповідає значенню  :
: .
. , який відповідає власному значенню
, який відповідає власному значенню  покладемо в (*)
покладемо в (*)  і отримаємо систему:
і отримаємо систему:
 .
. одержимо:
одержимо:  .
.
 в дану квадратичну форму, то отримаємо її канонічний вигляд. Цим можна скористатися для перевірки правильності розв’язку.
в дану квадратичну форму, то отримаємо її канонічний вигляд. Цим можна скористатися для перевірки правильності розв’язку. і знайти формули цього перетворення.
і знайти формули цього перетворення. або
або  ;
; .
. .
. нового базису.
нового базису. (α)
(α) (β)
(β)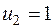 одержимо, що
одержимо, що 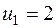 . Третя координата вектора може бути довільною. Нехай
. Третя координата вектора може бути довільною. Нехай  . Отримаємо вектор
. Отримаємо вектор  . Нормуючи цей вектор, одержимо один з шуканих векторів:
. Нормуючи цей вектор, одержимо один з шуканих векторів:
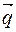 , ортогональний вектору
, ортогональний вектору 
 ;
;  можна взяти рівним будь-якому числу, відмінному від нуля, але, оскільки ми шукаємо одиничний вектор, краще вибрати
можна взяти рівним будь-якому числу, відмінному від нуля, але, оскільки ми шукаємо одиничний вектор, краще вибрати 
 , покладемо в системі (α)
, покладемо в системі (α)  . Отримаємо:
. Отримаємо: 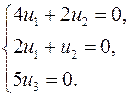
 . Нормуючи одержаний вектор
. Нормуючи одержаний вектор  , знайдемо вектор
, знайдемо вектор

 .
. .
.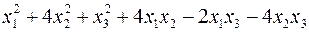 .
. .
. .
. .
. .
. .
. .
. .
.

 .
. .
.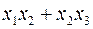 ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. привести до канонічного вигляду квадратичну форму і записати формули цього перетворення:
привести до канонічного вигляду квадратичну форму і записати формули цього перетворення: ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; .
. :
: .
. ;
;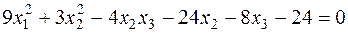 ;
; ;
; .
. .
. , (14)
, (14) , аналогічно
, аналогічно  Отже, еліпс – це фігура обмежена прямокутником із сторонами 2а і 2b.
Отже, еліпс – це фігура обмежена прямокутником із сторонами 2а і 2b. число а – велика піввісь
число а – велика піввісь – ексцентриситет (0<e<1),
– ексцентриситет (0<e<1), , називаються директрисами еліпса (не мають спільних точок з еліпсом).
, називаються директрисами еліпса (не мають спільних точок з еліпсом). . Так як точка М належить еліпсу, то її координати задовольняють рівняння еліпса:
. Так як точка М належить еліпсу, то її координати задовольняють рівняння еліпса:  , звідки y2=b2(1 –
, звідки y2=b2(1 –  ). Отже,÷ MF2 ÷ =
). Отже,÷ MF2 ÷ =  =
=  = =
= =  = ÷ ex+a ÷.
= ÷ ex+a ÷. Еліпсом називається множина всіх точок площини сума відстаней від яких до двох даних точок (фокусів) є величина постійна (рівна 2а).
Еліпсом називається множина всіх точок площини сума відстаней від яких до двох даних точок (фокусів) є величина постійна (рівна 2а).

 координат два концентричні кола радіусами a і b, a>b (рис.9).
координат два концентричні кола радіусами a і b, a>b (рис.9). , отже вона належить еліпсу.
, отже вона належить еліпсу. x=a cos φ,
x=a cos φ, φ <2p).
φ <2p). Очевидно, що точка N має координати N(2,у). Отже, отримаємо:
Очевидно, що точка N має координати N(2,у). Отже, отримаємо: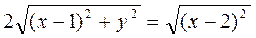 ,
, ,
, 

 ,
,

 ,
, (15)
(15)
 , або
, або  . Графік цієї функції необмежений і при х
. Графік цієї функції необмежений і при х 
 , наближається у першій четверті до прямої
, наближається у першій четверті до прямої  , яку називають асимптотою гіперболи.
, яку називають асимптотою гіперболи. e =
e =  >1 – ексцентриситет.
>1 – ексцентриситет.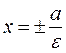 – директриси гіперболи.
– директриси гіперболи. – асимптоти гіперболи
– асимптоти гіперболи , і
, і Звідси випливає, що
Звідси випливає, що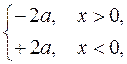 або ÷÷ MF1 ÷ –÷ MF2 ÷÷= 2a.
або ÷÷ MF1 ÷ –÷ MF2 ÷÷= 2a. .
. ,
,  ). Перейдемо до системи (O,
). Перейдемо до системи (O,  ′,
′,  ′), де (O,
′), де (O,  . Формули повороту прямокутних систем координат мають вигляд:
. Формули повороту прямокутних систем координат мають вигляд:  . Оскільки кут φ рівний -
. Оскільки кут φ рівний -  , або
, або 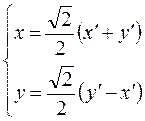 .
. , або
, або і
і  .
. і позначивши
і позначивши  отримаємо:
отримаємо: 
 , то ми отримаємо гіперболу, яка називається спряженою з
, то ми отримаємо гіперболу, яка називається спряженою з  . Вона має ті ж асимптоти, але її фокуси лежать на вісі OY (див. рис.12).
. Вона має ті ж асимптоти, але її фокуси лежать на вісі OY (див. рис.12). (16)
(16) Відмітимо основні елементи параболи, які не залежать від орієнтації системи координат:
Відмітимо основні елементи параболи, які не залежать від орієнтації системи координат: – фокальна відстань.
– фокальна відстань. ,0) – фокус.
,0) – фокус. – директриса.
– директриса. .
.  =÷ x+
=÷ x+  ÷.
÷.  отже,
отже,  , або
, або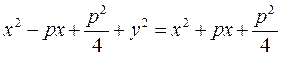 .
.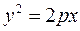 . Отже, якщо точка рівновіддалена від фокуса і директриси, то вона належить параболі (рис.13).
. Отже, якщо точка рівновіддалена від фокуса і директриси, то вона належить параболі (рис.13). а це і є відстань від точки М до директриси.
а це і є відстань від точки М до директриси. У прямокутній системі координат дана точка А(1,0) та пряма х = 2. Скласти рівняння лінії, кожна точка М(х,у) якої рівновіддалена від точки А та прямої х = 2.
У прямокутній системі координат дана точка А(1,0) та пряма х = 2. Скласти рівняння лінії, кожна точка М(х,у) якої рівновіддалена від точки А та прямої х = 2.

 .
.


