
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналітичне задання афінного перетворення. Група афінних перетвореньСодержание книги
Поиск на нашем сайте
Нехай
Визначник Зупинимося тепер на групі афінних перетворень та її підгрупах. Позначимо через А множину всіх афінних перетворень площини. Покажемо, що А – група. Розглянемо два афінних перетворення Тоді, за означення афінного перетворення, будь-які три точки А, В і С прямої перейдуть при перетворенні При перетворенні Таким чином послідовне виконання двох афінних перетворень Вона називається групою афінних перетворень площини. Група подібності площини
ЗАДАЧІ 1. Записати аналітичне задання паралельного перенесення на вектор 2. Знайти образ вісі ОХ при паралельному перенесенні на вектор 3. Знайти рівняння кола (x-2)2+(y+1)2=4 після паралельного перенесення на вектор 4. Записати аналітичне задання повороту навколо початку системи координат на кут 5. Знайти образ прямої х+2у+3=0 при повороті її навколо точки О(0,0) на кут 6. Отримати аналітичне задання центральної симетрії з центром в точці А(x0,y0). 7. Знайти образи точок М(1.3) і N(-5,2) при симетрії відносно точки А(4,5). 8. Знайти образ прямої х+5у–4=0 при симетрії відносно точки А(2,-3). 9. Отримати аналітичне задання повороту на кут 10. Знайти образ прямої 2х+3у-4=0 при осьовій симетрії відносно осі ОХ. 11. Знайти образ прямої 3х-5у+2=0 при гомотетії з центром в точці О(0,0) і коефіцієнтом m =5. 12. Отримати аналітичне задання гомотетії з центром в точці А(x0,y0) і коефіцієнтом k. 13. Записати аналітичне задання гомотетії з центром в точці А(4,1) і коефіцієнтом k=2. Знайти образ точки М(-1,5) при цій гомотетії. 14. Записати аналітичне задання центрально-подібного повороту з центром в точці О(0,0) на кут 15. Отримати аналітичне задання центрально-подібного повороту з центром в точці А(x0,y0). на кут 16. Аналітичне задання афінного перетворення має вигляд: Знайти: а) образи точок: O(0,0), A(-1,2), B(3,-7), b) образи векторів: с) прообрази точок: d) прообрази векторів: 17. Афінне перетворення задано формулами: Знайти: 1) образи прямих: а) вісі ОХ, б) вісі ОУ, в) 7х-7у+2=0. 2) прообрази прямих: а) вісі ОХ, б) вісі ОУ, в) 3х-2у-2=0. 18. Записати аналітичне задання афінного перетворення, яке три точки А(1,0), В(-2,1), С(-1,1) переводить відповідно в точки: а) б) 19. Записати аналітичне задання афінного перетворення, яке початок системи координат переводить в точку 20. Вияснити, які з перетворень є: 1) рухами; 2) подібністю, якщо вони задані наступними співвідношеннями: а) б) в) г) д) е) 21. Вияснити характер перетворення, якщо воно має аналітичне задання: 1) 2) 3) 4) 5) 6) 7) 8) 9) 22. Довести, що множина А(а) всіх афінних перетворень, для яких пряма а складається з нерухомих точок утворює групу. Розділ 2 Квадратичні форми
Поняття квадратичної форми
Відомо, що рівняння першої степені від двох змінних: Ax+By+C=0 визначає пряму лінію на площині, рівняння Ax+By+Cz+D=0 визначає площину у тривимірному векторному просторі. Аналогічно, в n –вимірному векторному просторі рівняння першої степені від n змінних визначає так-звану гіперплощину. Зустрічалися нам і рівняння кола та сфери, які є рівняннями другої степені. На площині нам відомі і інші лінії: гіпербола, парабола, еліпс. В просторі поверхні: циліндричні, канонічні і т. д. Зрозуміло що деякі криві і поверхні можуть мати рівняння і вище другої степені, але основні лінії: еліпс, парабола, гіпербола, та поверхні: сфера, еліпсоїд, параболоїди, гіперболоїди задаються якраз рівняннями другої степені. Відмітимо, що еліпс, парабола та гіпербола вивчалися ще стародавніми греками. Аполлоній описав їх основні властивості ще в третьому столітті до нашої ери. Ці криві часто використовуються в фізиці, астрономії, архітектурі. Лінією (кривою) другого порядку на площині будемо називати лінію, яка визначається рівнянням другої степені. Загальне рівняння другої степені від двох змінних має вигляд: a11x2+a22y2+2a12xy+2a13x+2a23y+a33=0, (7) де а11, а22, а12 не рівні нулю одночасно. Поверхнею другого порядку будемо називати поверхню, яка визначається рівнянням другої степені. Очевидно, що таке рівняння, в загальному випадку, має вигляд: a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+ +2a14x+2a24y+2a34z+a44=0, (8) де коефіцієнти а11, а22, а33, а12, а13, а23 не рівні нулю одночасно. Відмітимо, що при переході від однієї системи координат до іншої рівняння 2-го порядку перейде в рівняння 2-го порядку. Однією з основних задач аналітичної геометрії є зведення рівнянь (7) та (8) до канонічного вигляду: Ax¢ 2+By¢ 2=Q або Ax ¢ 2+By¢ 2+Cz¢ 2= Q, де Q – многочлен не вище першої степені. По аналогії з трьохвимірним векторним простором (див. § 17 [12]), можна отримати формули перетворення афінних систем координат в n– вимірному векторному просторі:
x2=c21y1+c22y2+…+c2nyn+c2, … … … … … … … … … … xn=cn1y1+cn2y2+…+cnnyn+cn, де нові базисні вектори і новий початок координат мають координати: Квадратичною формою від n –змінних x1, x2, …, xn називається однорідна функція другої степені від цих змінних, тобто функція вигляду: F (x)= Ясно, що в рівнянні (7) квадратична форма F(x)=a11x2+a22y2+2a12xy, а в рівнянні (8) F(x)=a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz. Квадратична форма називається канонічною, якщо вона має вигляд: § 13. Зведення квадратичної форми до канонічного вигляду в n -вимірному векторному просторі Теорема 6. У n-вимірномувекторному просторі завжди існує такий базис в якому квадратична форма (9) маєканонічний вигляд (10). Доведення: Розглянемо квадратичну форму (9): F(x)= Покажемо, що за допомогою заміни базису ця квадратична форма може бути приведена до канонічного вигляду. Скористаємося методом математичної індукції: 1. Нехай n=1 тоді F(x)=a11x 2. Нехай n >1. Будемо вважати твердження теореми вірним для квадратичної форми від меншого ніж n числа змінних. Розглянемо два випадки: a). Серед коефіцієнтів aii (i=1,…,n) квадратичної форми (9) є відмінні від нуля. Нехай, наприклад, а11¹ 0, тоді згрупуємо всі члени, які містять x1 і запишемо:
= a11x12+ Таким чином квадратичну форму F(x) можна записати так: F(x)= Позначимо:
y2=x2, Þ x2=y2, (11) ………….. …………… yn=xn. xn=yn. Після заміни базису за останніми формулами перетворення афінних систем координат, отримаємо квадратичну форму: F(y)= від n-1 змінної, яка за припущенням індукції приводиться до канонічного вигляду. б). Всі коефіцієнти квадратичної форми a11=a22=…=ann=0. Тоді існують коефіцієнти aij ¹ 0. В такому випадку потрібно так замінити базис, щоб появилися квадрати змінних. Нехай для конкретності а12¹ 0. Тоді квадратична форма F(x)=2a12x1x2+…. Використаємо формули перетворення афінних систем координат:
x2=y1 – y2, x3=y3, (12) ......... xn=yn. Після заміни базису, отримаємо: F(y)=2a12(y12 – y22)+…. Отже, в квадратичній формі появилися квадрати змінних і маємо перший випадок.
Приклад 1. Привести квадратичну форму до канонічного вигляду і знайти базис у якому вона має такий вигляд: а) Розв’язання. Оскільки квадрати змінних в даній квадратичній формі відсутні, то маємо випадок б) теореми 6. Скористаємося формулами (12):
Отримаємо Згрупуємо всі додатки, які містять
Згідно формул (11) в цьому випадку отримаємо формули переходу до нової системи координат:
В новій системі координат квадратична форма має канонічний вигляд:
Так як базис замінювався двічі, то загальні формули перетворення отримаємо, підставивши рівності (**) в (*). Одержимо:
Таким чином квадратична форма b) Розв’язання. Згрупуємо всі доданки, які містять
Після заміни базису отримаємо:
Формули відповідного перетворення систем координат матимуть вигляд:
Згрупувавши доданки, які містять
Після заміни базису за формулами:
Загальні формули перетворення афінних систем координат, які зводять квадратичну форму
Базисні вектори нової системи координат:
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 915; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.239.25 (0.007 с.) |

 – дане афінне перетворення. Виберемо на площині афінний репер R і точку М з координатами х і у у цьому репері. Тоді, згідно теореми 5, репер R перейде при перетворенні
– дане афінне перетворення. Виберемо на площині афінний репер R і точку М з координатами х і у у цьому репері. Тоді, згідно теореми 5, репер R перейде при перетворенні  , а точка М в точку
, а точка М в точку  з такими ж координатами х і у в
з такими ж координатами х і у в  . Позначимо
. Позначимо  і
і  координати точки
координати точки  в репері R. Потрібно виразити
в репері R. Потрібно виразити  і
і  через х і у. Таким чином, задача зводиться до звичайної задачі перетворення афінних систем координат (див. § 15[12]): точка
через х і у. Таким чином, задача зводиться до звичайної задачі перетворення афінних систем координат (див. § 15[12]): точка  в старому репері має координати
в старому репері має координати  ,
,  , а в новому х, у, виразити
, а в новому х, у, виразити  ,
,  (8)
(8) – якщо афінне перетворення першого роду,
– якщо афінне перетворення першого роду,  – афінне перетворення другого роду.
– афінне перетворення другого роду.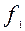 і
і  .
. причому просте відношення
причому просте відношення 
 і
і  перейдуть в точки
перейдуть в точки  і (
і (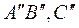 ) = (
) = (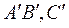 ).
). і
і  = (АВ,С), тобто композиція двох афінних перетворень є афінним перетворенням. Замкненість доведено. Покажемо, що якщо
= (АВ,С), тобто композиція двох афінних перетворень є афінним перетворенням. Замкненість доведено. Покажемо, що якщо  , то і
, то і  .(існування оберненого) Дійсно, якщо точки
.(існування оберненого) Дійсно, якщо точки  належать одній прямій, то за означенням і їх образи
належать одній прямій, то за означенням і їх образи  також належать одній прямій і
також належать одній прямій і  Отже, множина
Отже, множина  всіх афінних перетворень площини утворює групу.
всіх афінних перетворень площини утворює групу. і група
і група  всіх рухів площини є підгрупами групи А. Очевидно, що і всі їх підгрупи є також підгрупами групи А. Неважко перевірити, що існують і інші підгрупи групи А. Наприклад, множина
всіх рухів площини є підгрупами групи А. Очевидно, що і всі їх підгрупи є також підгрупами групи А. Неважко перевірити, що існують і інші підгрупи групи А. Наприклад, множина 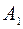 всіх афінних перетворень першого роду; множина
всіх афінних перетворень першого роду; множина  всіх афінних перетворень для яких
всіх афінних перетворень для яких  – нерухома точка (група центрально-афінних перетворень); множина
– нерухома точка (група центрально-афінних перетворень); множина  всіх афінних перетворень, для яких пряма а складається з нерухомих точок.
всіх афінних перетворень, для яких пряма а складається з нерухомих точок. =(-3,5). Знайти образ при такому паралельному перенесенні: а) точки М(2,3), б) прямої 4х–у+7=0, в) прямої 5х+3у–11=0.
=(-3,5). Знайти образ при такому паралельному перенесенні: а) точки М(2,3), б) прямої 4х–у+7=0, в) прямої 5х+3у–11=0. =(4,7).
=(4,7). =(5,-1).
=(5,-1). . Знайти образ точки М(2,-3) при цьому повороті.
. Знайти образ точки М(2,-3) при цьому повороті.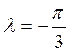 .
. навколо точки А(x0,y0). Знайти образ точки М(5,0) після повороту навколо точки А(-1,3) на кут
навколо точки А(x0,y0). Знайти образ точки М(5,0) після повороту навколо точки А(-1,3) на кут  .
. і коефіцієнтом k=2. Знайти образи точок М(
і коефіцієнтом k=2. Знайти образи точок М( ) і N(0,-2) при цьому перетворенні.
) і N(0,-2) при цьому перетворенні. з коефіцієнтом k.
з коефіцієнтом k.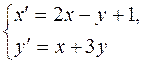
 .
. =(-3,.2),
=(-3,.2), 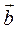 =(-1,0),
=(-1,0),  =(5,3).
=(5,3). .
.
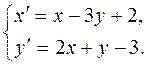


 , а всі точки прямої 3х+4у+1=0 залишає нерухомими.
, а всі точки прямої 3х+4у+1=0 залишає нерухомими.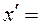 2х,
2х, 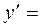 2у;
2у; 3х,
3х, 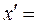
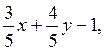

 ;
; х,
х,  у;
у; 8х-у+1,
8х-у+1,  х+8у.
х+8у. -х+1,
-х+1,  -у;
-у;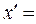

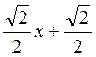 ;
;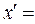 -х-6,
-х-6,  -5у,
-5у, 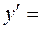 5х;
5х; 5у;
5у;

 ;
; 3х+1.
3х+1. x1=c11y1+c12y2+…+c1nyn+c1,
x1=c11y1+c12y2+…+c1nyn+c1, = (c11, c21,..., cn1), …,
= (c11, c21,..., cn1), …,  = (c1n, c2n,..., cnn ),
= (c1n, c2n,..., cnn ),  в старому базисі.
в старому базисі.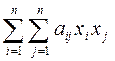 ,де (aij=aji) (9)
,де (aij=aji) (9) (10)
(10)
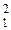 отже, квадратична форма в канонічному вигляді.
отже, квадратична форма в канонічному вигляді. (a11x1+a12x2+…+a1nxn)2=a11x12+2a12x1x2+…+2a1nx1xn+A=
(a11x1+a12x2+…+a1nxn)2=a11x12+2a12x1x2+…+2a1nx1xn+A= + A, де А – многочлен, який не містить x1.
+ A, де А – многочлен, який не містить x1.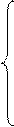
 y1=a11x1+a12x2+…+a1nxn, x1=
y1=a11x1+a12x2+…+a1nxn, x1=  y2 –…–
y2 –…–  yn ,
yn , y12+G(y2,y3,…,yn), де G(y2,y3,…,yn) квадратична форма
y12+G(y2,y3,…,yn), де G(y2,y3,…,yn) квадратична форма .
. (*)
(*)
 (за теоремою 6, випадок а) отримаємо):
(за теоремою 6, випадок а) отримаємо): .
. (**)
(**)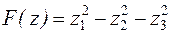 .
.
 матиме канонічний вигляд
матиме канонічний вигляд 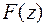 в базисі:
в базисі:  ,
,  ,
, 
 .
. (за теоремою 6 випадок а):
(за теоремою 6 випадок а):
 .
.
 (аналогічно до попереднього), отримаємо:
(аналогічно до попереднього), отримаємо: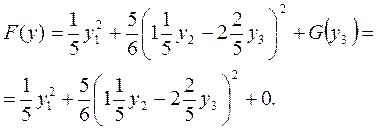
 отримаємо квадратичну форму в канонічному вигляді:
отримаємо квадратичну форму в канонічному вигляді: 
 до канонічного вигляду
до канонічного вигляду  .
.
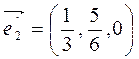 ,
,  .
.


