
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи Рунге – Кутта з вищими порядками похибкиСодержание книги
Поиск на нашем сайте
Чи існують методи Рунге – Кутта з порядком похибки s = 3, якщо q = 2? Спочатку більш докладно розглянемо підрахунки § 5. При q = 2 уk+1 = yk + p1w1(h) + p2w2(h) = yk + p1h f (xk, yk) + p2h f ( звідки φk(0) = 0. Похідні функції φk(h): φk´(h) = p1 f (xk, yk) + p2 f ( φk´´(h) = 2p2 ( φk´´´(h) = 3p2((α2)2 φk´´´(0) = (3p2(α2)2 – 1) Як і в інших розділах, наприкінці наведемо без доведення результати для більш складних випадків. Спочатку нехай q = 3. Тоді існує вже 8 параметрів: p1, p2, p3, α2, α3, β21, β31, β32. Метод Рунге – Кутта з q = 3 має третій порядок точності (тобто φk(0) = φk´(0) = φk´´(0) = φk´´´(0) = 0) тоді і тільки тоді, коли
p3β32α2 =
Ця система шести рівнянь з вісьма невідомими має безліч розв’язків. Найбільш поширена така сукупність розрахункових формул: w1(h) = h f (xk, yk), w2(h) = h f (xk + w3(h) = h f (xk + h, yk – w1(h) + 2w2(h)), уk+1 = yk + p1w1(h) + p2w2(h) + p3w3(h). Якщо права частина функції f (x, y) не залежить від у, тобто уk+1 = yk + Розрахункових формул для порядку точності s = 4 з q = 3 не існує. Для порядку точності s = 5 не існує розрахункових формул з q = 4 і q = 5. При q = 4 існує двопараметрична множина розрахункових формул, відповідна порядку точності s = 4. Для прикладу наведемо одно однопараметричне сімейство таких формул: w1(h) = h f (xk, yk), w2(h) = h f (xk + w3(h) = h f (xk + w4(h) = h f (xk + h, yk + (1 – t)w2(h) + tw3(h)), уk+1 = yk + Найбільш застосовуваною є сукупність формул цього сімейства, яка відповідає t = 1: w1(h) = h f (xk, yk), w2(h) = h f (xk + w3(h) = h f (xk + уk+1 = yk + Треба зазначити, що формулювання “найбільш застосовувана” відповідає історичній тенденції у використанні чисельних методів. Якщо деякий метод виявився прийнятним, то користувачі звикають до нього і неохочі до його заміни на дещо більш ефективний. Крім того, не існує єдиного критерію переваги алгоритму. Наприклад, може виявитися, що метод з меншою похибкою є більш чутливим до обчислювальної похибки. Як правило тому, для заміни “найбільш застосовуваного” методу на інший потрібна суттєва перевага його над попередником.
Питання, тести 1. Якщо функція f (x, y) і її часткова похідна
2. Розв’язати задачу Коші чисельно означає для заданої послідовності х0, х1, …, хn значень незалежної змінної х знайти числову послідовність у0, у1, …, уn так, щоб
3. Чисельний розв’язок задачі Коші у´(х) = 2, y(0) = 1 має на відрізку [0; 1] найкращі (тобто найменші) похибки наближеного значення для заданих точок хi, якщо
4. Для чисельного розв’язку задачі Коші у´(х) = – 2, y(0) = 1 на відрізку [0; 2] похибка наближеного значення для заданої точки хi = 1 дорівнює
5. Чисельний розв’язок задачі Коші у´(х) = 2х – 1, y(0) = 1 на відрізку [0; 1] серед двох методів: Ейлера та удосконаленого методу Ейлера має найкращі (тобто найменші) похибки наближеного значення для заданих точок хi, якщо
6. Метод Ейлера – це ітераційний метод, рекурентна формула якого має вигляд:
7. Рекурентна формула удосконаленого методу Ейлера має вигляд:
8. Чисельні розв’язки задачі Коші у´(х) = 2у +
А:
Б:
В:
Г:
9. Чисельні розв’язки задачі Коші у´(х) = 2у + А:
Б:
В:
Г:
10. Методами Рунге – Кутта називають ітераційні методи, які визначаються рекурентними формулами уk+1 = yk +
11. Якщо s є порядком точності методу Рунге – Кутта, то похибка цього методу на кроці дорівнює
12. Збіжність методу тим швидше, чим порядок його точності
13. Чи до кожної задачі Коші у´ = f (x, y); у(х0) = у0, для якої виконуються умови теореми існування та єдності розв’язку можна застосувати формули Рунге – Кутта?
14. Який порядок точності методу, що визначається рекурентними формулами xk+1 = xk + h, уk+1 = уk +
15. Який порядок точності методу Рунге – Кутта чисельного розв’язання задачі Коші А:
Б:
19. Формули методу кратного перерахунку – це
20. У стовпці В наступної таблиці знаходяться наближені значення чисельного розв’язку задачі Коші методом Рунге – Кутта другого порядку точності для заданої точки хi = 1 з кроками h = 0,2 0,1 0,05 0,025 у чарунках В2, В3 В4 і В5 відповідно. Така таблиця здійснює подвійний перерахунок цих даних: А:
Б:
В:
Г:
20. У стовпці В наступної таблиці знаходяться наближені значення чисельного розв’язку задачі Коші методом Рунге – Кутта третього порядку точності для заданої точки хi = 1 з кроками h = 0,2 0,1 0,05 0,025 у чарунках В2, В3 В4 і В5 відповідно. Така таблиця здійснює кратний перерахунок цих даних: А:
Б:
В:
Г:
Завдання 1. Знайти чисельні розв’язки задачі Коші у´(х) = 2у + 2. Знайти чисельні розв’язки задачі Коші у´(х) = 2у + 3. Знайти чисельні розв’язки задачі Коші 4. Знайти чисельний розв’язок задачі Коші
Іменний покажчик Адамс 5 Банах 104, 156 Бессель 47, 48 Гаусс 5, 49, 135-138, 140, 142, 143, 145, 148, 149, 153 - 156, 164-168, 170-172, 183, 185, 186, 192 Гейзенберг 65 Ейлер 5, 234-239, 241-245, 250, 252, 253, 262-264,267,271 Ейткін 28-31, 34, 37, 53, 54, 58 Ерміт 5; Жордан 192-195, 197, 198, 211, 212, 215, 217, 218, 221, 230, 233 Зейдель 160-163 Котес 67-69, 71-73, 76, 79, 87, 88, 90 Кутт 242-247, 249, 253, 259, 260, 262, 265-269, 271 Лагранж 17-20, 25, 28, 50-52, 67, 75, 98, 104, 121, 248 Левер’є 5 Лейбниц 62, 65 Ліпшиць 104-108, 115, 129 Лобачевський 5 Ловелл 5; Ньютон 5, 6, 19, 21, 23-25, 27, 28, 35-37, 39-41, 43, 45, 46, 48, 51-53, 56-58, 60, 65, 67-69, 71-73, 87, 88, 111-116, 118, 120-125, 131, 132, 134, 171 Річардсон 4, 72, 74, 75, 78, 81, 88, 89, 246, 248, 249; 267 Рунге 4, 72, 74, 77, 78, 81, 88, 89, 242-249, 252, 253, 255, 256, 259, 260, 262, 265, 266, 268, 269, 271 Сімпсон 68-71, 79, 80, 87, 88, 90, 93, 94, 260 Стірлінг 47 Тейлор 8, 9, 19, 50, 111, 116, 243 Чебишов 34
Предметний покажчик *Методи обчислень – це алгоритми знаходження чисельних (доведених до числових відповідей) розв’язків типових математичних задач. А саме рівнянь (диференціальних в тому числі), систем рівнянь і нерівностей, задач аналізу (диференціювання, інтегрування, наближення функцій), задач оптимізації тощо(сторінка 3, 5, 156) *Нехай а – точне значення деякої величини, а* - відоме наближення до нього. Абсолютною похибкою (погрішністю) наближення а* називають таку величину Δ(а*), для якої * Задача називається коректно поставленою, якщо для будь-яких вхідних даних з деякого класу існує єдиний і стійкий за вхідними даними її розв‘язок. Наведена вище задача обчислення інтегралів є коректно поставленою на множині неперервних функцій, а диференціювання – некоректно поставленою задачею на множині диференційовних функцій. (сторінка 12) * Задачею інтерполяції (або інтерполювання) є побудова такої функції, яка для даних значень аргументу приймає задані значення. (сторінка 9) * Наближену рівність f (x) ≈ Рn(х) називають інтерполяційною формулою. Різницю Rn(f,x) = f (x) – Рn(х) називають залишковим членом інтерполяційної формули або похибкою інтерполювання(сторінка 9.10.12.14.16.17.21.22.23.25.27.29.32.35.36.37) * Квадратурні формули – це формули вигляду * З алишковий член R(f) квадратурної формули Ньютона – Котеса має порядок k (де k – натуральне число) відносно кроку інтегрування h, якщо існують такі сталі С, с > 0, що chk ≤ ôR(f)ô ≤ Сhk для всіх достатньо малих h.(.22.32.39.40.43-47.55.56) * Розв‘язати рівняння * Нехай R – метричний простір, ρ – відстань (метрика) на цьому просторі, А – оператор, визначений на R. Оператор А називають оператором стиску, якщо існує таке додатне число q < 1, що ρ(Ах, Ах′) < q ∙ ρ(х, х′) для будь – яких х, х′ є R. Точку х є R називають нерухомою точкою оператора А, якщо Ах = х. (68,81,82) * Оптимальним розв’язком задачі (f, V, Ω) називається таке х0 є Ω, що f (x0) ≤ f (x) (або f (x0) ≥ f (x)) для всіх х є Ω. Оптимізаційну задачу називають нерозв’язною, якщо вона не має оптимальних розв’язків. Розв’язати оптимізаційну задачу означає або знайти всі її оптимальні розв’язки, або ж довести її нерозв’язність. (116,120,121,125,127,128129,131134,142,143,145,146-150,152,153,157) *Оптимізаційна задача (f, V, Ω), у якій цільова функція f є лінійною на V, а Ω є множиною розв’язків деякої системи лінійних рівнянь і нерівностей називають задачею лінійного програмування. Систему лінійних рівнянь і нерівностей, яка визначає Ω, називають системою обмежень задачі лінійного програмування(116,119,120-125,127,128,131,132,134,135-139,146,148,152,153,154,155,157,158) * Крайньою точкою опуклої множини V називається така точка х є V, що будь – яка опукла комбінація х = λ∙y + μ∙z, де у,z є V, λ, μ ≥ 0, λ + μ = 1 можлива лише за умови, що у = z = х. Матриця А системи (1) вимірності m × n
називається матрицею умов, стовпці А1, А2, …, Аn цієї матриці – векторами умов, а вектор В називається вектором обмежень задачі (1). (121,124,125,) *Задача лінійного програмування має канонічну форму, якщо всі її змінні невід’ємні, а всі інші умови системи обмежень – рівняння (тобто у (1) m1 = m, n1 = n). (123) * Опорним розв’язком задачі лінійного програмування у канонічній формі називають такий допустимий розв’язок її системи обмежень, у якому всі вільні змінні дорівнюють нулю. 2) Опорний розв’язок називають невиродженим, якщо всі його основні змінні додатні, в противному разі опорний розв’язок називають виродженим. Традиційним є таке еквівалентне. Опорним розв’язком задачі (2) називається її допустимий розв’язок, якщо вектори умов з номерами його додатних координат утворюють лінійно незалежну систему векторів. (116,119,120-125,127,128,131,132,134,135-139,146,148,152,153,154,155,157,158)
*Базисом опорного розв’язку називають такий базис векторів умов, який містить всі вектори умов, що відповідають додатним координатам цього розв’язку.(127) * Отриманутаблицю називають симплекс – таблицею, приведеною до базису * Задача Коші для звичайного диференціального рівняння першого порядку у´ = f (x, y); у(х0) = у0 (1) полягає в тому, щоб знайти розв’язок у(х) цього рівняння, який задовольняє початкову умову у(х0) = у0. (159,160,161,165,167,168) *1) Розв’язати задачу (1) чисельно означає для заданої послідовності х0, х1, …, хn значень незалежної змінної х і числа у0 знайти числову послідовність у0, у1, …, уn так, щоб уk з заданою точністю наближав у(хk) для всіх k, де у(х) – єдиний розв’язок задачі Коші з початковою умовою у(х0) = у0. 2) Різницю уk – у(хk) називають похибкою наближеного значення уk в точці хk. 3) Якщо всі точки х0, х1, …, хn рівновіддалені: хk = х0 + kh, то величину h називають кроком інтегрування диференціального рівняння. (159,160,161,165,167,168)
* Величину φk(h) = уk+1 – у(хk+1) = yk +
Література
1. Лященко М.Я., Головань М.С., Чисельні методи – К: Либідь,1996 р. 2. Бахвалов Н.С., Жидков Н.П., Кобельков Т.М., Численные методы – М: Наука,1987 г. 3. Волков Е.А., Численные методы – М: Наука, 1978 г. 4. Жалдак М.І., Рамський Ю.С., Чисельні методи математики – К: Радянська школа,1984 р. 5. Заварыкин В.М., Житомирский В.Г., Лапчик М.П., Вычислительная математика – М.: Просвещение, 1990 г. 6. Назаренко О.М. Основи економетрики – К: Центр навчальної літератури, 2004 р. 7. Бабенко К.И., Основы численного анализа – М: Наука, 1986 г. 8. Бахвалов Н.С. Численные методы – М; Наука, 1973г. т. 1. 9. Борозин Ч.С., Жидков Н.П., Методы вычислений – М: Наука, 1956г. т.1, 1962г. т.2. 10. Демидович Б.П., Марон И.А., Основы вычислительной математики – М: Физматгиз, 1958г. 11. Ляшко И.И., Макаров В.Л., Скоробогатько А.А., Методы вычислений К: Вища школа, 1977 г.
З м і с т
Передмова ……………………………………………………………………………….. 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.017 с.) |

 ,
,  ), де
), де 
 +
+ 
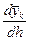 ) – у´(хk + h) = p1 f (xk, yk) + p2 f (
) – у´(хk + h) = p1 f (xk, yk) + p2 f ( (
( + 2α2β21
+ 2α2β21  (
( (
( )´ =
)´ =  + 2
+ 2  f ´ =
f ´ =  + (6p2α2β21 – 2)
+ (6p2α2β21 – 2)  α2 = β21, α3 = β31 + β32, α3(α3 – α2) – β32α2(2 – 3 α2) = 0,
α2 = β21, α3 = β31 + β32, α3(α3 – α2) – β32α2(2 – 3 α2) = 0, , p2α2 + p3α3 =
, p2α2 + p3α3 =  , p1 + p2 + p3 = 1.
, p1 + p2 + p3 = 1. , yk +
, yk +  ),
), (f (xk) + 4 ∙ f (xk +
(f (xk) + 4 ∙ f (xk +  –
–  )w1(h) +
)w1(h) +  (x, y) неперервні у точці (х0; у0), то для звичайного диференціального рівняння першого порядку у´ = f (x, y)
(x, y) неперервні у точці (х0; у0), то для звичайного диференціального рівняння першого порядку у´ = f (x, y)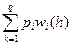 , де
, де h f (хk; уk)?
h f (хk; уk)? на відрізку [1; 2] з кроком інтегрування у чарунці H1, якщо він визначається такими формулами:
на відрізку [1; 2] з кроком інтегрування у чарунці H1, якщо він визначається такими формулами: +
+ 
 , де
, де  , і оцінити похибку отриманого розв’язку методом подвійного перерахунку.
, і оцінити похибку отриманого розв’язку методом подвійного перерахунку. на відрізку [0; 1] методом Рунге – Кутта другого порядку точності за формулою
на відрізку [0; 1] методом Рунге – Кутта другого порядку точності за формулою 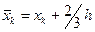 з точністю 10-4, оціненою методом кратного перерахунку.
з точністю 10-4, оціненою методом кратного перерахунку. . Відносною похибкою (погрішністю) називають таку величину δ(а*), що
. Відносною похибкою (погрішністю) називають таку величину δ(а*), що  . (сторінка 7)
. (сторінка 7) ≈
≈  . Суму в правій частині формули
. Суму в правій частині формули  означає знайти множину всіх його коренів (тобто таких значень х є [a;b], при яких воно стає числовою тотожністю) або ж довести, що їх не існує. Розв‘язок (корінь) рівняння
означає знайти множину всіх його коренів (тобто таких значень х є [a;b], при яких воно стає числовою тотожністю) або ж довести, що їх не існує. Розв‘язок (корінь) рівняння  називають ще нулем функції
називають ще нулем функції  . (61.64.71.89)
. (61.64.71.89)
 ,
, 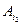 , …,
, …,  опорного розв’язку α, а числа δj – оцінками цього базису або оцінками її основних (базових) змінних
опорного розв’язку α, а числа δj – оцінками цього базису або оцінками її основних (базових) змінних 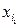 ,
,  , …,
, …,  . (148-150.155)
. (148-150.155)


