
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерполювання із скінченими різницями за допомогою ExcelСодержание книги
Поиск на нашем сайте
Означення 10. Якщо вузли інтерполяції хk = х0 + kh, де h – дійсна стала, k = 0,1,…,n, yk = f (хk), то таблицю
називають горизонтальною таблицею її скінчених різниць. Задача 1. Знайти для функції f, заданої таблицею
її скінчені різниці Δ2у3 , Δ4у3, Δ5у0 . Розв’язання. Побудуємо таблицю скінчених різниць, звідки й отримаємо шукані значення. Надамо чарункам електронної таблиці таких значень:
У рядку 1 указані порядки скінчених різниць у відповідному стовпці. У стовпці B тут різниці порядку 0, тобто значення функції f у вузлі інтерполяції, номер якого вказаний у стовпці А. Правила копіювання Excel дозволяють отримати у відповідних чарунках саме ті формули, які повинні там бути згідно з попереднім означенням: так у чарунці Е4 міститься Δ3у2. В результаті отримаємо таку трикутну таблицю:
Тут Δ3у2 ≈ 0,0019, Δ5у0 ≈ – 0,0022, скінчена різниця Δ4у3 не визначена умовами задачі. Задача 2. Для функції f, заданої таблицею
знайти наближені значення функції в точках x1* = 0,1 і x2* = 1,1. Розв’язання. Побудуємо спочатку таблицю скінчених різниць, за якою знайдемо інтерполяційний многочлен Ньютона. Оскільки дана в умові таблиця відрізняється від таблиці в умові задачі 1 тільки доданим шостим вузлом інтерполяції, то і таблицю скінчених різниць цієї задачі можна отримати з такої таблиці попередньої задачі, просто продовживши її копіювання:
В результаті отримаємо таку трикутну таблицю:
Оскільки в даному випадку x1* = 0,1 міститься на початку таблиці, тобто x1* є [x0; x1], то тут доцільно буде скористатися формулою Ньютона дляінтерполюваннявперед, тобто першою інтерполяційною формулою Ньютона (3). У ній задіяні тільки скінчені різниці Δkу0, які всі містяться у рядку 2 останньої таблиці. За умовою t = (x1* – x0)/h = (0,1 – 0)/0,2 = 0,5. Побудуємо таблицю для підрахунків Lk(x1*) (k = 1,…,6). Надамо таких значень чарункам електронної таблиці:
Тут у рядку 11 позначений номер k одночлена uk(x) =
Отже, відповідь f (0,1) ≈ L6(0,1) ≈ 0,099619. Щодо x2* = 1,1, то це значення міститься ближче до кінця відрізкаінтерполювання, x2* є [x5; x6]. Тож тут доцільно скористатися формулою Ньютона дляінтерполювання назад, тобто другою інтерполяційною формулою Ньютона (4). У ній задіяні тільки скінчені різниці Δkуn-k (k = 1,…,n), які за означенням 9 всі містяться на діагоналі горизонтальної таблиці скінчених різниць. Оскільки зручніше для подальших підрахунків тримати всі ці значення на горизонталі, то таблицю скінчених різниць дещо переформуємо у порівнянні з означенням 10:
Зауваження. Традиційно цю останню таблицю записують у такому форматі:
Природно, що таку таблицю звичайно називають діагональною. Однак нам зручніше буде використовувати її для розрахунків у попередньому форматі. Отже, надамо чарункам електронної таблиці таких значень:
В результаті отримаємо ту ж саму таблицю скінчених різниць у новому форматі:
Побудуємо таблицю для підрахунку Lk(x2*). Тут за умовою t = (x2* – x6)/h = (1,1 – 1,2)/0,2 = – 0,5. Надамо чарункам електронної таблиці таких значень:
Вона майже не відрізняється від копії таблиці для підрахунку Lk(x1*) у нові чарунки: лише у чарунці В28 нове значення t = – 0,5, у формулі чарунки С28 заміняємо – на + і у чарунці В31 посилаємось на таблицю скінчених різниць у новому форматі. В результаті отримаємо таку таблицю:
Шукане значення L6(x2*) у чарунці H32. Отже, відповідь f (1,1) ≈ L6(1,1) ≈ 0,833. Задача 3. Оцінити похибку інтерполяції у задачі 2, якщо вважати, що функція f (x) 9 разів неперервно диференційовна і задана таблицею
Розв’язання. Згідно з теоремою 3 абсолютна похибка інтерполяції R6(f,x) за першою інтерполяційною формулою Ньютона це R6(f,x) = f (x) – L6(x) ≈
В результаті отримаємо таку трикутну таблицю:
Побудуємо таблицю для підрахунку L7(x1*):
В результаті отримаємо таку таблицю:
Абсолютна похибка інтерполяції R6(f,x) = u7(x) міститься у чарунці I15: R6(f,x) ≈ 2,23∙10-5. Отже, результат отриманий з табличною точністю чотирьох вірних значущих цифр. Аналогічно абсолютна похибка інтерполяції R6(f,x) за другою інтерполяційною формулою Ньютона це R6(f,x) = f (x) – L6(x) ≈
В результаті отримаємо таку трикутну таблицю:
Побудуємо таблицю для підрахунку L7(x2*):
В результаті отримаємо:
Абсолютна похибка інтерполяції R6(f,x) = u7(x) міститься у чарунці I31: R6(f,x) ≈ 2,2∙10-5. Отже, результат і тут отриманий з табличною точністю чотирьох вірних значущих цифр. Означення 11. Емпіричною формулою називають наближену формулу, отриману інтерполяцієютаблиці експериментальних даних.
Задача 4. Побудувати емпіричну формулу для функції f, заданої таблицею
Розв’язання. С початку складемо за даною таблицею електронну горизонтальну таблицю скінчених різниць:
Виявляється, що у стовпці G всі різниці п’ятого порядку з табличною точністю (чотири вірні значущі цифри) дорівнюють нулю. За означенням 7 скінчені різниці вищих порядків автоматично також нулі з такою точністю. Всі різниці четвертого порядку у стовпці F це стала 0,4 з точністю 10-4. За наслідком з леми 2 §6 на відрізку інтерполяції f (x) ≈ Lm(x), де Lm(x) – інтерполяційний многочлен степеня m = 4 у будь – якій формі. Отже, тут у якості емпіричної формули природно застосувати першу інтерполяційну формулу Ньютона. В даному випадку за таблицею скінчених різниць це f (x) ≈ L4(x) ≈ 0,1t – 0,0019
Інші методи інтерполювання Для інтерполювання значення х функції, що знаходиться поблизу вузла хi у середині таблиці з рівновіддаленими вузлами інтерполяції з кроком h, звичайно використовують формулу Стірлінга, якщо │t│= │x – хi│/h ≤ 0,25 або формулу Бесселя, якщо 0,25 ≤│t│≤ 0,75. У цьому випадку зручно позначити цей найближчий вузол через х0, а індекси інших вузлів рахувати так, як указано у наступній таблиці (де уk = f (хk)):
Формула Стірлінга має вигляд Ln(x) = у0 + t Якщо t = 1/2, то формула Бесселя значно спрощується і в такому разі називається формулою інтерполювання на середину: Ln(x) = Зокрема при n = 1 отримаємо формулу квадратичної інтерполяції по Бесселю: L1(x) = у0 + tΔу0 – При інтерполюванні функцій з великою кількістю вузлів інтерполяційний многочлен має високій степінь, що спричиняє коливання на проміжках між вузлами. Щоб зменшити степінь інтерполяційного многочлена вузли інтерполювання можна розбити на групи і проводити інтерполювання по групах. Але в цьому разі порушуються аналітичні умови, з’являються точки розриву похідних. Позбутися цього недоліку можна за допомогою сплайнів – функцій, які гладко склеєні з різних частин многочленів заданого степеня. Розіб’ємо заданий відрізок [a; b] на n частин точками а = х0 < х1 < … < хn = b. Сплайном Sm(x) називається функція, що визначена на відрізку [a; b] і має на ньому неперервну похідну порядку m – 1, а на кожному відрізку [хk; хk+1] співпадає з деяким многочленом степеня не вище за m, причому хоча би на жодному з них степінь точно дорівнює m. Сплайн, який у вузлах хk приймає ті ж самі значення, що й деяка функція f (x) називається інтерполяційним. На практиці широко застосовують сплайни третього степеня (кубічні сплайни S3(x)). Для побудови інтерполяційного кубічного сплайну розіб’ємо відрізок [a; b] на n рівних частин довжини h = (b – а)/ n. В цьому разі на відрізку [хk; хk+1] (k = 0,1,…n – 1) кубічний сплайн запишеться так: S3(x) = + де mk, mk+1 – деякі числа. Виявляється, що саме за такої формули S3(хk) = f (хk), S3(хk+1) = f (хk+1), S´3(хk) = mk, S´3(хk+1) = mk+1, що і визначає цю формулу. Отже, кубічний сплайн S3(x) має неперервну першу похідну всюди на [a; b]. Тепер оберемо числа mk так, щоби S3(x) мав і другу неперервну похідну на [a; b]. Ця умова зводиться до умови рівності другої похідної зліва і справа у кожному вузлі хk (k = 1,…,n – 1), вона приймає вигляд: mk-1 + 4mk + mk+1 =
Матриця цієї системи не вироджена і тому вона має єдиний розв’язок. Розв’язати її можна методом Гаусса або будь – яким іншим методом розділу 3. Знайшовши mk, побудувати інтерполяційний кубічний сплайн можна за формулою (5) на кожному відрізку [хk; хk+1] (k = 0,1,…,n) окремо. Доведено, що кубічна сплайн – функція – це єдина функція Р(х) з мінімальною кривиною серед усіх функцій, які інтерполюють дану функцію f (x), тобто у всіх вузлах інтерполяції задовольняють умови Р(x0) = f (x0), …, Р(xn) = f (xn), і мають квадратично інтегровну другу похідну. Отже, в цьому розумінні кубічний сплайн найкраща з функцій, які інтерполюють дану функцію.
Питання, тести
1. Задача інтерполювання функції з n вузлами інтерполяції має єдиний розв’язок, якщо інтерполююча функція Р(х) – це
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.98.190 (0.01 с.) |

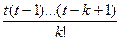 Δkу0 першого інтерполяційного многочлена Ньютона Lk(x). У чарунці В12 значення кроку t = 0,5 вузлів інтерполяції. У рядку 13 підраховуються множники t(t – 1)(t – 2)…(t – k + 1) з номером k, позначеним у рядку 11. У рядку 14 підраховуються значення факторіалу k! з відповідним для цього стовпця номером k. У рядку 15 знаходимо значення одночлена uk(x) з відповідним стовпцю номером k у заданій точці x1*. Нарешті у рядку 16 послідовно знаходимо суми одночленів uk(x1*), шукане значення L6(x1*) дістанемо у чарунці H16. В результаті отримаємо таку таблицю:
Δkу0 першого інтерполяційного многочлена Ньютона Lk(x). У чарунці В12 значення кроку t = 0,5 вузлів інтерполяції. У рядку 13 підраховуються множники t(t – 1)(t – 2)…(t – k + 1) з номером k, позначеним у рядку 11. У рядку 14 підраховуються значення факторіалу k! з відповідним для цього стовпця номером k. У рядку 15 знаходимо значення одночлена uk(x) з відповідним стовпцю номером k у заданій точці x1*. Нарешті у рядку 16 послідовно знаходимо суми одночленів uk(x1*), шукане значення L6(x1*) дістанемо у чарунці H16. В результаті отримаємо таку таблицю: t(t – 1)(t – 2)…(t – 7). Це останній одночлен u7(x) першого інтерполяційного многочлена Ньютона L7(x). Отже, для отримання похибки інтерполяції необхідно просто продовжити таблиці задачі 2 ще на восьмий вузол:
t(t – 1)(t – 2)…(t – 7). Це останній одночлен u7(x) першого інтерполяційного многочлена Ньютона L7(x). Отже, для отримання похибки інтерполяції необхідно просто продовжити таблиці задачі 2 ще на восьмий вузол: – 0,0017
– 0,0017  + 0,0004
+ 0,0004 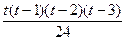 , де t = (х – x0)/h = (х – 0)/0,1 = 10х, звідки L4(x) ≈ х – 0,19
, де t = (х – x0)/h = (х – 0)/0,1 = 10х, звідки L4(x) ≈ х – 0,19  – 1,7
– 1,7  + 4
+ 4 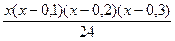 ≈ х – 0,1х(х – 0,1) – 0,3х(х – 0,1)(х – 0,2) + 0,173х(х – 0,1)(х – 0,2)(х – 0,3).
≈ х – 0,1х(х – 0,1) – 0,3х(х – 0,1)(х – 0,2) + 0,173х(х – 0,1)(х – 0,2)(х – 0,3). +
+  Δ2у-1 +
Δ2у-1 + 
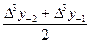 +
+  Δ4у-2 +
Δ4у-2 + 
 +
+  Δ6у-3 + … +
Δ6у-3 + … +  Δ2nу-n, де t = (х – х0)/h. Формула Бесселя має вигляд Ln(x) =
Δ2nу-n, де t = (х – х0)/h. Формула Бесселя має вигляд Ln(x) =  + (t –
+ (t –  )Δу0 +
)Δу0 +  +
+  Δ3у-1 +
Δ3у-1 +  ∙
∙  +
+  Δ5у-2 +
Δ5у-2 + 
 + … + +
+ … + + 
 + +
+ +  Δ2n+1у-n, де t = (х – х0)/h.
Δ2n+1у-n, де t = (х – х0)/h.
 ∙
∙ 

 (Δу1 – Δу-1). Електронні таблиці для підрахунків значень інтерполяційного многочлена аналогічні таким таблицям для формул Ньютона.
(Δу1 – Δу-1). Електронні таблиці для підрахунків значень інтерполяційного многочлена аналогічні таким таблицям для формул Ньютона. +
+ , (5)
, (5) (f (хk+1) – f (хk)), (k = 1,…,n – 1). Це система n – 1 лінійних рівнянь відносно n + 1 невідомих mk (k = 0,1,…,n). Для однозначного визначення невідомих додають ще дві умови: це умови обмежень на значення сплайна і його похідних на кінцях відрізка [a; b], які і називають крайовими. Існує декілька видів крайових умов, одна з найпоширеніших це S´3(а) = f ´(а), S´3(b) = f ´(b). Тоді система n + 1 лінійних рівнянь відносно n + 1 невідомих mk (k = 0,1,…,n) має вигляд:
(f (хk+1) – f (хk)), (k = 1,…,n – 1). Це система n – 1 лінійних рівнянь відносно n + 1 невідомих mk (k = 0,1,…,n). Для однозначного визначення невідомих додають ще дві умови: це умови обмежень на значення сплайна і його похідних на кінцях відрізка [a; b], які і називають крайовими. Існує декілька видів крайових умов, одна з найпоширеніших це S´3(а) = f ´(а), S´3(b) = f ´(b). Тоді система n + 1 лінійних рівнянь відносно n + 1 невідомих mk (k = 0,1,…,n) має вигляд:



