
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод подвійного перерахунку.Содержание книги
Поиск на нашем сайте
Нехай залишковий член деякої узагальненої квадратурної формули Ньютона – Котеса має порядок р відносно кроку інтегрування h: R(f) = О(hр). Поділимо відрізок [a; b] на n рівних відрізків і на 2n рівних відрізків, нехай In та I2n – відповідні наближені значення інтеграла 1. R2n (f) ≈ 2. Назва екстраполяція пов’язана з тим, що коли In ≠ I2n, то уточнене значення In,2n ніколи не лежить між In та I2n. Справді, якщо I2n > In, то з (15) випливає, що In,2n > I2n = max{ In, I2n }. Якщо ж I2n < In, то In,2n < I2n = min{ In, I2n }. Формул (14) і (15) достатньо для практичної реалізації методу подвійного перерахунку (див. наступний параграф). Тут далі наведені обґрунтування цих формул і водночас їх точне формулювання. Функцію f (х) будемо вважати диференційовною стільки разів, скільки це виявиться необхідним. Спочатку зазначимо, що оскільки 1) завжди залишковий член квадратурної формули Ньютона – Котеса на відрізку [a; b] R(f) = R(f) = f (m+1)(ξ) де h = b – a – довжина відрізку, а Нехай задана деяка узагальнена квадратурна формула Ньютона – Котеса порядку р відносно кроку інтегрування h: R(f) = О(hр). Поділимо відрізок [a; b] на n рівних відрізків завдовжки h = (b – a)/n точками a = х0 < х1 < … < хk < … < хn = b і на 2n рівних відрізків завдовжки h/2 = (b – a)/2n точками a = y0 < y1 < … < yk < … < y2n = b так, щоби хk = y2k (k = 0, 1, …, n). За означенням узагальненої квадратурної формули до кожного з відрізків [хk; хk+1] застосуємо дану неузагальнену формулу Ньютона – Котеса і отримаємо відповідні наближені значення Ink інтеграла
I = In + Rn(f) = In + I = I2n + R2n(f) = I2n + Спочатку при кожному k знехтуємо відмінністю між Мnk, М2n2k і М2n2k+1 – значеннями функції f (m+1)(х) на відрізку [хk; хk+1] довжини h ® 0 і покладемо Мnk ≈ М2n2k ≈ М2n2k+1 ≈ Мk, М = I = In + Rn(f) = In + M I = I2n + R2n(f) = I2n + 2M Відомими в (19) є In, I2n, h і р, невідомими I та С. Отже, це система двох лінійних рівнянь з двома невідомими. Звідси I2n + С( формули, єдине неточне припущення у доведенні – рівність Мnk ≈ М2n2k ≈ М2n2k+1 ≈ Мk. Отже, покладемо Мk = Мnk, Δ2n2k = М2n2k – Мk = f (m+1)(ξ2n2k) – f (m+1)(ξnk) = f (m+2)(η 2n2k) ∙ (ξ2n2k – ξnk), де за теоремою Лагранжа η 2n2k Î [ ξ2n2k; ξnk ] Í [хk; хk+1], звідки ôΔ2n2kô ≤ теоремою Лагранжа ôΔ2n2kô ≤ I = In + Rn(f) = In + M I = I2n + R2n(f) = I2n + (2M + Δ) Як і раніше, звідси I2n + С(
1. R2n (f) = Поділимо відрізок [a; b] на n, на 2n і на 4n рівних відрізків, дістанемо In,2n і аналогічно I2n,4n:
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.212.181 (0.01 с.) |

 за цією квадратурною формулою, а Rn(f) і R2n(f) – відповідні залишкові члени. Метод подвійного перерахунку ґрунтується на двох формулах.
за цією квадратурною формулою, а Rn(f) і R2n(f) – відповідні залишкові члени. Метод подвійного перерахунку ґрунтується на двох формулах. (правило Рунге) (14)
(правило Рунге) (14) , де Rm(f, х) = f (х) – Lm(x) – це залишковий член відповідної інтерполяційної формули, а 2) згідно з теоремою 1 розділу Rm(f, х) =
, де Rm(f, х) = f (х) – Lm(x) – це залишковий член відповідної інтерполяційної формули, а 2) згідно з теоремою 1 розділу Rm(f, х) = 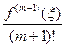 ωm+1(х), де ξ = ξ (x) є [a; b], то і R(f) =
ωm+1(х), де ξ = ξ (x) є [a; b], то і R(f) =  , де ξ Î [a; b]. Справді, оскільки
, де ξ Î [a; b]. Справді, оскільки 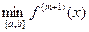
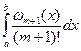 ≤ R(f) ≤
≤ R(f) ≤ 
 = f (m+1)(ξ)
= f (m+1)(ξ)  hm+2, (16)
hm+2, (16) , х =
, х =  +
+  t, хj =
t, хj =  та залишкові члени Rnk(f). Згідно з висновком § 5Rnk(f) = О(hр+1), згідно з (16) Rnk(f) = f (m+1)(ξnk)
та залишкові члени Rnk(f). Згідно з висновком § 5Rnk(f) = О(hр+1), згідно з (16) Rnk(f) = f (m+1)(ξnk)  та I2n2k+1 інтеграла
та I2n2k+1 інтеграла 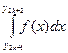 і відповідні залишкові члени R2n2k(f) та R2n2k+1(f): R2n2k(f) = О(
і відповідні залишкові члени R2n2k(f) та R2n2k+1(f): R2n2k(f) = О( )p+1 , R2n2k+1(f) = О(
)p+1 , R2n2k+1(f) = О( =
= 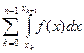 =
=  = In,
= In, 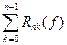 = Rn(f) =
= Rn(f) =  ∙
∙ 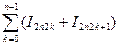 = I2n,
= I2n, 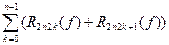 = R2n(f) =
= R2n(f) =  ∙
∙  , С = M
, С = M  ∙h. Аналогічно Δ2n2k+1 = М2n2k+1 – Мk = f (m+1)(ξ2n2k+1) – f (m+1)(ξnk), звідки за
∙h. Аналогічно Δ2n2k+1 = М2n2k+1 – Мk = f (m+1)(ξ2n2k+1) – f (m+1)(ξnk), звідки за = 2М + Δ, де Δ =
= 2М + Δ, де Δ = 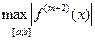 ∙h = 2
∙h = 2  B(
B( = R2n,4n (f) + О(hp+2), тобто відрізняється від R2n,4n (f) на величину порядку на одиницю більшу за порядок R2n,4n (f). Звідси
= R2n,4n (f) + О(hp+2), тобто відрізняється від R2n,4n (f) на величину порядку на одиницю більшу за порядок R2n,4n (f). Звідси 


