
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ейлера за допомогою ExcelСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У наступній задачі дістанемо чисельні розв’язки деякої задачі Коші спочатку методом Ейлера, потім удосконаленим методомЕйлера і порівняємо отримані результати. Задача 1. 1) Знайти чисельні розв’язки задачі Коші у´(х) = 2у + 2) Знайти удосконаленим методомЕйлера чисельні розв’язки тої ж задачі Коші з тими ж кроками інтегрування, що й в 1). Розв’язання. 1)Кроки інтегрування задамо у чарунках H1: H4 так, що H1 = 0,2, а H4 = 0,025. Побудуємо електронну таблицю для чисельного розв’язання даної задачі Коші з кроком інтегрування 0,2 методомЕйлера. Надамо чарункам таких значень:
Тут у чарунках А2:В2 координати початкової точки, у чарунці С2 підраховується кутовий коефіцієнт f (х0; у0), помножений на крок інтегрування, у стовпці А отримуються значення хk з кроком 0,2 на відрізку [0; 1]. Тоді у стовпці В будуть обчислені відповідні значення у(хk) згідно з рекурентною формулою (1). (Як і завжди, символ ↓ тут означає копіювання попередніх чарунок). В результаті отримаємо таку таблицю:
Звичайно, стовпець А копіюємо лише до чарунки із значенням 1, в даному випадку до А7. Звідси у(0,2) ≈ 1,315853, у(1) ≈ 4,604125. Для отримання аналогічної таблиці з кроком інтегрування 0,1 можна скопіювати попередні формули, наприклад у діапазон Е1:G3, як це зробили ми, а потім у чарунках Е3 і G2 у $H$1 замінити 1 на 2. Таким чином отримуємо таку таблицю:
І тоді в результаті обчислень дістанемо:
Так само скопіюємо попередні формули у два нових вільних діапазони, (скажімо у А9:С11 та J1:L3, як це зробили ми), а потім у відповідних чарунках замінимо в $H$1 1 відповідно на 3 і 4. В результаті дістанемо:
Тепер побудуємо електронну таблицю для чисельного розв’язання даної задачі Коші з кроком 0,2 удосконаленим методомЕйлера. Надамо чарункам таких значень:
Формули у стовпцях А, В, С майже ідентичні відповідним формулам таблиці методу Ейлера, лише чарунці В3 надана формула = B2 + F2 замість = B2+C2 у методі Ейлера. Але в цьому й врахована відмінність цих методів, у стовпці В обраховуються значення згідно з (2): уk+1 = уk + f (хk +
Далі можна, як і в методі Ейлера, скопіювати попередні формули, наприклад у діапазон J1:O3, а потім у чарунках A3, C2, D2, F2 у $H$1 замінити 1 на 2, звідки дістанемо:
І тоді в результаті обчислень дістанемо:
Так само скопіюємо попередні формули у два нових вільних діапазони, а потім замінимо в $H$1 1 відповідно на 3 і 4 у відповідних чарунках. В результаті отримуємо таблиці:
та
Такими є результати обрахунків. Оскільки похибка на кожному кроці є систематичною, то найбільшу похибку слід очікувати у кінцевій точці 1. Тому порівняємо тепер наближені значення розв’язку задачі Коші, отримані в задачі методом Ейлера та удосконаленим методомЕйлера саме у цій точці за допомогою наступної таблиці.
Тут у стовпці h використані в попередній задачі кроки інтегрування диференціального рівняння.
Методи Рунге – Кутта Природно запитати: якщо в рекурентній формулі удосконаленого методуЕйлера уk + ½ = уk + У найбільш загальному вигляді задача ставиться так. Нехай відомим є значення yk = у(хk) розв’язку задачі Коші (1) в довільній точці хk, h – крок інтегрування, треба наближено обчислити у(хk+1) – точне значення розв’язку в наступній точці хk+1 = хk + h. В процесі обчислень фіксовані деякі числа (параметри) p1, …, pq, α2, …, αq, βij 0 < j < i ≤ q. Тоді Означення 3. Формули для обчислення наближеного значення уk+1 розв’язку в точці хk+1 уk+1 = yk + w1(h) = h f (xk,yk), w2(h) = h f (хk + α2h, yk + β21w1(h)), ………………………………………………………………………………… wq(h) = h f (xk + αqh, yk + βq1w1(h) + βq2w2(h) + … + βqq-1wq-1(h)) називають формулами Рунге – Кутта. Відповідні ітераційні методи за цими рекурентними формулами називають методами Рунге – Кутта. У цих формулах враховані практично всі можливі удосконалення методу Ейлера і треба так підібрати параметри, щоб збіжність відповідного методу була найшвидша можлива. Спочатку надамо точного змісту словам про найшвидшу збіжність методу. Величина φk+1(h) = уk+1 – у(хk+1) = yk + Означення 4. 1.Величину φk(h) = уk+1 – у(хk+1) = yk + 2. Якщо при даних фіксованих параметрах φk(0) = φk´(0) = … = φk(s)(0) = 0 для всіх достатньо гладких f (x, y), що визначають відповідну задачу Коші (1), а φk(s+1)(0) ≠ 0 для деякої гладкої f (x, y), то натуральне число s називають порядком точності методу. Іншими словами, s є порядком точності методу, якщо похідні наближення уk+1 = yk + φk(h) = Отже, Очевидно, що збіжність методу буде найшвидшою, якщо порядок його точності буде найбільшим. Отже, наша мета – так підібрати параметри, щоб порядок точності виявився найбільшим можливим. При q = 1 маємо лише один параметр p1 (оскільки для βij 0 < j < i ≤ q, звідки при q = 1 0 < j < 1, а такого натурального j не існує). Тому уk+1 = yk + p1w1(h) = yk + p1h f (xk,yk), φk(h) = уk+1 – у(хk+1) = yk + p1h f (xk,yk) – у(хk + h). Звідси φk(0) = 0; φk´(0) = p1 f (xk, yk) – у´(хk + h)׀h=0 = (p1 – 1) f (xk,yk), оскільки у´(хk + h)׀h=0 = у´(хk) = f (xk,yk); φk´´(0) = – у´´(хk). Очевидно, що рівність φk´(0) = 0 для всіх f (xk,yk) буде виконана лише за умови, що p1 = 1. За такої умови уk+1 = yk + h f (xk,yk), що співпадає з (1), тобто це формула методу Ейлера. Отже,
Висновок 1. 1) Метод Ейлера – це метод Рунге – Кутта з q = 1. 2) Метод Рунге – Кутта з q = 1 має перший порядок точності тоді і тільки тоді, коли це метод Ейлера. 3) Похибка методу Ейлера на кроці має вигляд φk(h) = – Пункт 3) випливає безпосередньо з (4), оскільки, очевидно, φk´´(h) = – у´´(хk + h), звідки φk´´(θh) = – у´´(хk + θh). Розглянемо тепер випадок q = 2. Тоді маємо чотири параметри: p1, p2, α2, β21. Тому уk+1 = yk + p1w1(h) + p2w2(h) = yk + p1h f (xk, yk) + p2h f ( φk´(h) = p1 f (xk, yk) + p2 f ( Звідси, оскільки Отже, рівність φk´(0) = 0 для всіх f (xk,yk) буде виконана лише за умови, що p1 + p2 – 1 = 0. φk´´(h) = 2p2 ( φk´´(0) = 2p2 ( Але у´´(хk) = (у´(хk))´ = φk´´(0) = 2p2 ( Отже, рівність φk´´(0) = 0 для всіх f (xk, yk) буде виконана лише за умов 2p2α2 – 1 = 0, 2p2β21 – 1 = 0. Рівність φk´(0) = 0 для всіх f (xk,yk) виконана за умови, що p1 + p2 – 1 = 0. Рівність φk(0) = 0 виконана автоматично завжди. Висновок 2. 1) Метод Рунге – Кутта з q = 2 має другий порядок точності (тобто φk(0) = φk´(0) = φk´´(0) = 0) тоді і тільки тоді, коли
p2α2 = p2β21 =
2) Якщо p2 = 1, то звідси p1 = 0, α2 = β21 = (Тут уk + ½ = Апріорні оцінки похибок чисельних наближень уk до точних значень розв’язків у(хk) в точках заданої послідовності хk, які безпосередньо випливають з (4), як правило, значно завищені. Крім того, іноді оцінити значення
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.139 (0.013 с.) |

 sin(3x – y), y(0) = 1 на відрізку [0; 1] з кроками інтегрування h = 0,2 0,1 0,05 0,025 методомЕйлера.
sin(3x – y), y(0) = 1 на відрізку [0; 1] з кроками інтегрування h = 0,2 0,1 0,05 0,025 методомЕйлера. ; уk + ½)h, а доданок f (хk +
; уk + ½)h, а доданок f (хk + 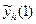

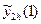 , наприклад, для методу Ейлера
, наприклад, для методу Ейлера  = 0,612698 =
= 0,612698 =  –
– 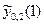 = 5,216823 – 4,604125. З таблиці відразу видно, що значення
= 5,216823 – 4,604125. З таблиці відразу видно, що значення 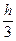 : уk + ⅓ = уk +
: уk + ⅓ = уk + 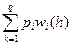 , де
, де hi +
hi + 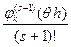 hs+1 =
hs+1 =  hs+1 ≤ ôφk(h)ô ≤
hs+1 ≤ ôφk(h)ô ≤  hs+1, тобто величина похибки методу на кроці має порядок s + 1: φk(h) = О(hs+1). Але з переходом від кроку до кроку ця похибка систематично зростає і на відрізку завдовжки одиниця сумарна похибка методу є O(hs), оскільки ітерацій з кроком інтегрування h на такому відрізку порядку
hs+1, тобто величина похибки методу на кроці має порядок s + 1: φk(h) = О(hs+1). Але з переходом від кроку до кроку ця похибка систематично зростає і на відрізку завдовжки одиниця сумарна похибка методу є O(hs), оскільки ітерацій з кроком інтегрування h на такому відрізку порядку  . Таким чином, порядок точності методу завжди на одиницю менший, ніж порядок його похибки на кроці. Так порядок точності методу Ейлера дорівнює одиниці, бо на одному кроці похибка цього методу має порядок h2, а порядок точності удосконаленого методу Ейлера дорівнює двом, оскільки на одному кроці похибка цього методу має порядок h3.
. Таким чином, порядок точності методу завжди на одиницю менший, ніж порядок його похибки на кроці. Так порядок точності методу Ейлера дорівнює одиниці, бо на одному кроці похибка цього методу має порядок h2, а порядок точності удосконаленого методу Ейлера дорівнює двом, оскільки на одному кроці похибка цього методу має порядок h3. ,
,  ), де
), де 
 +
+ 
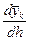 ) – у´(хk + h) = p1 f (xk, yk) + p2 f (
) – у´(хk + h) = p1 f (xk, yk) + p2 f ( (
(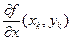 α2 +
α2 + 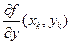 β21 f (xk, yk)) – у´´(хk).
β21 f (xk, yk)) – у´´(хk).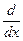 f (x, y(х))ôx = xk, y = yk =
f (x, y(х))ôx = xk, y = yk =  p1 + p2 = 1
p1 + p2 = 1


