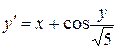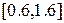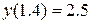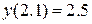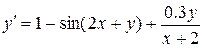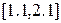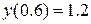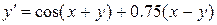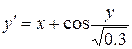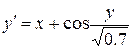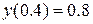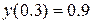Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ейлера-Коші з ітераціямиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Метод Ейлера-Коші з ітераціями належить до неявних однокрокових методів і полягає в обчисленні на кожному кроці початкового значення:
Запишемо за допомогою ітераційної формули:
де
де Зазвичай кількість ітерацій не має перевищувати 3-4, в противному випадку необхідно зменшити крок Приклад 5.2 Знайти методом Ейлера-Коші значення Рішення. Обчислимо за формулою (5.7) значення
За формулою (5.8) знайдемо:
Знайдемо
Отже, за значення □ Модифікований метод Ейлера Модифікований метод Ейлера є одно кроковим методом другого порядку, який реалізуються формулами:
Метод дає похибку, пропорційну Метод Рунге-Кута Метод Рунге-Кута – однокроковий метод розв’язку звичайних диференціальних рівнянь, на якому побудовані різницеві схемі різного порядку точності. Двочленна формула має вид:
де
Для
Чотиричленна формула Рунге-Кута
Явні методи Адамса Метод Адамса належить до числа
Значення Формула явного трикрокового методу Адамса:
Для явного чотири крокового методу Адамса формула має вид:
Приклад 5.3 Знайти Рішення. За формулою
За формулою (5.14) отримаємо:
□ Завдання на проведення лабораторної роботи 1) Використовуючи методи Адамса (два-, три-, чотирикрокові), розв’язати звичайне диференціальне рівняння першого порядку на відрізку 2) Розв’язати звичайне диференціальне рівняння першого порядку на відрізку 3) Всі обчислення проводити з чотирма десятковими знаками після коми. 4) Навести блок-схеми алгоритмів методів, які було використано в роботі. Зміст звіту В звіті з лабораторної роботи необхідно навести: – загальні відомості щодо чисельних методів розв’язку звичайних диференціальних рівнянь, які використано в роботі; – розв’язок рівнянь вказаними методами; – порівняння і аналіз отриманих результатів. 5.4 Контрольні питання 1. В чому полягає відмінність однокрокових методів від багатокрокових, явних від неявних? 2. За яких значень коефіцієнтів формули Рунге-Кута можна отримати метод Ейлера та його модифікації? 3. Чим визначається похибка методів? 4. В який спосіб пов’язані похідні функції та її розділені різниці? 5. При розв’язку яких задач використовуються чисельні методи розв’язку звичайних диференціальних рівнянь?
Таблиця 5.1 – Варіанти ЗДР для розв’язку числовими методами
Література 1. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: "Наука", 1970. – 288 с. 2. Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране. – М.: Изд-во МГУ, 1990. – 336 с. 3. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. – М.: Наука, 1986. – 288 с. 4. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение. – М.: Мир, 1998. – 575 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 988; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 . (5.7)
. (5.7) , (5.8)
, (5.8) ,
, 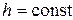 , розв’язок уточнюється. Ітерації проводять доти, поки не буде виконана умова:
, розв’язок уточнюється. Ітерації проводять доти, поки не буде виконана умова: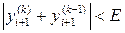 ,
, – задана точність.
– задана точність.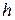 , наприклад
, наприклад  , і повторити обчислення
, і повторити обчислення  з початку. Похибка методу пропорційна
з початку. Похибка методу пропорційна  .
. для диференціального рівняння з прикладу 5.1.
для диференціального рівняння з прикладу 5.1. :
: .
.

 :
:  ,
, .
. ,
, . (5.9)
. (5.9) .
. , (5.10)
, (5.10) ,
, ,
,
 ,
, .
.
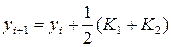 ,
, , (5.11)
, (5.11) ,
, , (5.12)
, (5.12) ,
, .
. -крокових методів. Розглянемо явний двокроковий метод Адамса, що полягає в обчисленні на кожному кроці
-крокових методів. Розглянемо явний двокроковий метод Адамса, що полягає в обчисленні на кожному кроці  . (5.13)
. (5.13)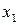 при цьому необхідно обчислити будь-яким однокроковим методом того ж самого, або більш високого порядку точності.
при цьому необхідно обчислити будь-яким однокроковим методом того ж самого, або більш високого порядку точності. (5.14)
(5.14) . (5.15)
. (5.15) трикроковим методом Адамса для задачі Коші
трикроковим методом Адамса для задачі Коші 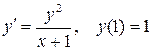 на відрізку
на відрізку 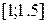 з
з 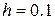 . Початкові значення
. Початкові значення  обчислити методом Ейлера-Коші.
обчислити методом Ейлера-Коші. знайдемо
знайдемо  :
:
 .
. , крок
, крок  , крок
, крок