
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання на проведення лабораторної роботиСодержание книги
Поиск на нашем сайте
1) Скласти таблицю значень функції, наведеної в таблиці 2.3, розбивши заданий інтервал на 5 відрізків з 2) Скласти горизонтальну таблицю кінцевих різностей. 3) За першою і другою інтерполяційними формулами Ньютона, використовуючи горизонтальну таблицю різностей, визначити значення функції в точках:
4) Побудувати емпіричну формулу для заданої функції. 5) Скласти таблицю значень функції, розбивши заданий інтервал на 10 відрізків. З отриманої таблиці взяти значення 6) Побудувати інтерполяційну формулу Лагранжа. 7) Визначити значення функції за інтерполяційною формулою Лагранжа в точках п. 3). 8) Обчислити похибку розрахунків. 9) Навести блок-схеми алгоритмів методів, які було використано в роботі.
Таблиця 2.3 – Варіанти завдань
Зміст звіту У звіті з лабораторної роботи необхідно навести: - короткі теоретичні відомості; - рішення завдань лабораторної роботи; - аналіз результатів і висновки по лабораторній роботі. 2.4 Контрольні питання 1. Мета і постановка задачі інтерполяції функції. 2. В чому полягає і як розв’язується задача інтерполяції? 3. Як побудувати інтерполяційний многочлен за 1-ою і 2-ю формулами Ньютона? 4. Як побудувати інтерполяційний поліном за формулою Лагранжа? 5. Які особливості інтерполяційної формули Лагранжа? 6. Як розраховуються коефіцієнти полінома Лагранжа у випадку рівновіддалених вузлів інтерполяції? 7. Як обчислити похибку інтерполяції деякої функції поліномом Лагранжа? Література 1. Демидович Б.П, Марон И.А. Основы вычислительной математики. 3-е изд., испр. – М.: Наука, 1966. – 664 стр. 2. Краскевич В.Е., Зеленский К.Х., Гречко В.И. Численные методы инженерных исследований. – Киев: Высшая шк., 1986. – 263 стр. 3. Боглаев Ю.П. Вычислительная математика и программирование – М.: Высш. шк., 1990. – 544 стр.
Тема: Чисельне інтегрування. Мета: Отримати практичні навики розв’язку задач чисельного інтегрування. Ідея: Навчитися складати квадратурні формули чисельного інтегрування. За допомогою різних формул обчислити інтеграл заданої функції та похибку. Порівняти між собою використані формули.
Загальні відомості Постановка задачі
Дана неперервна функція Якщо відома первісна
В багатьох практичних випадках первісна функція не може бути знайдена за допомогою елементарних засобів чи є занадто складною; крім того, на практиці підінтегральна функція часто задається таблицею. В цих випадках застосовують методи наближеного обчислення інтегралів.
Методи розв’язку задачі Звичайним прийомом чисельного обчислення інтеграла є заміна функції Замінюючи підінтегральну функцію будь-яким многочленом, отримуємо квадратурні формули типу
де
Кажуть, що, відкидаючи
де Розіб’ємо відрізок Квадратурні формули для рівнозначних вузлів називають формулами Ньютона-Котеса.
Формули наближеного інтегрування
Формула прямокутників
Геометричною інтерпретацією інтегралу від заданої функції
Рисунок 3.1 – Геометрична інтерпретація формули лівих прямокутників
Щоб збільшити точність обчислення інтегралу, відрізок
Формула лівих прямокутників (рис.3.1):
Формула правих прямокутників (рис.3.2):
Рисунок 3.2 – Геометрична інтерпретація формули правих прямокутників
Формула середніх прямокутників (рис. 4.3)
Рисунок 3.3 – Геометрична інтерпретація формули середніх прямокутників
Приклад 3.1. Розрахувати інтеграл Рішення.
Похибка:
Формула трапецій Площа, що обчислюється, може бути представлена також у вигляді суми площин трапецій
Рисунок 3.4 – Геометрична інтерпретація формули трапецій Приклад 3.2. Розрахувати інтеграл Рішення.
Залишковий член:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.167.244 (0.008 с.) |



 і скласти нову таблицю значень функції.
і скласти нову таблицю значень функції.
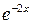






 )
)



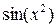












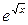
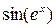






 Лабораторна робота №3
Лабораторна робота №3 . Розрахувати із заданою похибкою
. Розрахувати із заданою похибкою 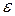 значення певного інтеграла від цієї функції на відрізку
значення певного інтеграла від цієї функції на відрізку  .
. заданої функції
заданої функції  , то інтеграл від функції
, то інтеграл від функції  (3.1)
(3.1)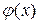 простого виду. Функція
простого виду. Функція  обчислювався безпосередньо.
обчислювався безпосередньо. (3.2)
(3.2)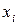 – обрані вузли інтерполяції;
– обрані вузли інтерполяції; – коефіцієнти, що залежать від вибору вузлів, але не від виду функцій;
– коефіцієнти, що залежать від вибору вузлів, але не від виду функцій;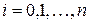 ;
; – залишковий член, який характеризує похибку квадратурної формули.
– залишковий член, який характеризує похибку квадратурної формули. , (3.3)
, (3.3) – значення інтегралу, обчисленого за допомогою формули наближеного інтегрування,
– значення інтегралу, обчисленого за допомогою формули наближеного інтегрування,  – точне значення інтегралу. Точним значенням інтегралу від заданої функції будемо вважати значення отримане за формулою Ньютона-Лейбниця, або якщо не існує первісної функції
– точне значення інтегралу. Точним значенням інтегралу від заданої функції будемо вважати значення отримане за формулою Ньютона-Лейбниця, або якщо не існує первісної функції 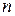 рівних частин. Отримуємо систему рівнозначних вузлів
рівних частин. Отримуємо систему рівнозначних вузлів 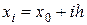 ,
,  . Значення функцій в цих точках дорівнюють
. Значення функцій в цих точках дорівнюють  .
.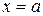 ,
,  , віссю абсцис та графіком функції. За наближене значення цієї площі можна взяти площу прямокутника зі сторонами:
, віссю абсцис та графіком функції. За наближене значення цієї площі можна взяти площу прямокутника зі сторонами: ,
,  – формула лівих прямокутників;
– формула лівих прямокутників; – формула правих прямокутників;
– формула правих прямокутників; – формула середніх прямокутників.
– формула середніх прямокутників.
 вузлів
вузлів  загальний вид формул прямокутників і їх геометрична інтерпретація наведені нижче.
загальний вид формул прямокутників і їх геометрична інтерпретація наведені нижче. (3.4)
(3.4)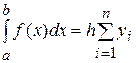 (3.5)
(3.5)
 (3.6)
(3.6)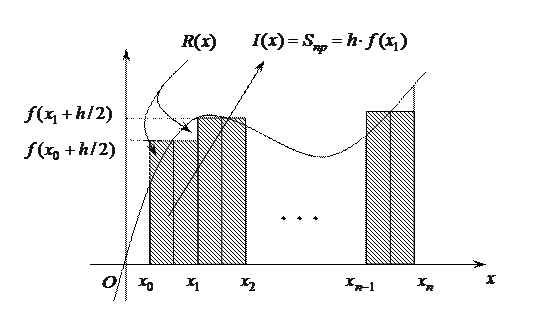
 за формулою лівих прямокутників,
за формулою лівих прямокутників,  .
.



 ;
;  ;...;
;...; 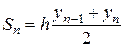
 (3.7)
(3.7)





