
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Сімпсона (формула парабол)Содержание книги
Поиск на нашем сайте
Інтеграл являє собою суму площин під параболами, кожна з яких проводиться через три сусідні точки, тобто параболи займають два сусідніх відрізки, наприклад
Рисунок 3.5 – Геометрична інтерпретація формули парабол
Зауваження. Формула прямокутників є точною для багаточлена нульового ступеня, формула трапецій дає точне значення інтеграла, коли підінтегральна функція Приклад 3.3. Розрахувати інтеграл Рішення.
Залишковий член:
Формула Гауса Для отримання підвищеної точності при чисельному інтегруванні використовують формулу Гауса.
У (3.9) не фіксуються не лише вузли інтерполяції При цьому Значення Таблиця 3.1 – Значення
Для обчислення інтеграла загального вигляду
Тоді формула Гауса матиме вигляд
При цьому забезпечується точність для багаточлена ступеня до
Приклад 3.4. Обчислити інтеграл Рішення. Тут
Квадратурні коефіцієнти попарно рівні:
Тоді остаточно отримуємо
Зауваження. Для функцій, що мають достатню кількість похідних, формула Гауса забезпечує найбільшу точність, а формула Сімпсона точніша за формулу трапецій.
Завдання на проведення лабораторної роботи
1) Вивчити формули для наближеного обчислення інтегралів і формули похибок. 2) Обчислити інтеграл з 3) Навести блок-схеми алгоритмів методів, які було використано в роботі.
Зміст звіту У звіті з лабораторної роботи необхідно навести: – формули наближеного інтегрування; – обчислення інтеграла за формулами і результат розрахунку;
– точне значення заданого інтегралу і похибки чисельного інтегрування; – аналіз результатів і висновки з роботи.
3.4 Контрольні питання
1. В чому полягає задача чисельного інтегрування? Як вона втілюється в різноманітних формулах чисельного інтегрування? 2. В яких випадках використовується чисельне інтегрування? 3. Як оцінити похибку наближеного обчислення інтегралів? 4. Вкажіть області застосування формул трапецій, Сімпсона, Гауса.
Література 1. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966. – 664с. 2. Копченова Н.В., Марон И.В. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 512с. 3. Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высш. шк., 1990, – 544с. Лабораторна робота №4 Тема: Обчислювальні методи розв’язку алгебраїчних і трансцендентних рівнянь. Мета роботи: навчитися розв’язувати рівняння з однією змінною, використовуючи обчислювальні методи. Ідея: навчитися відокремлювати корені, уточнювати їх за допомогою різних методів, усвідомити принцип методу ітерацій.
Теоретичні відомості Постановка задачі Задане рівняння з однією змінною
де функція Розв’язати рівняння означає знайти множину його коренів, тобто таких значень Знайти точне значення кореня заданого рівняння можна тільки для найпростіших функцій Задача знаходження коренів рівняння (4.1) вважається вирішеною, якщо корені обчислені з наперед заданою точністю. Нехай Пошук наближених коренів рівняння (4.1) складається з двох етапів: 1) відділення коренів, тобто знаходження достатньо малих відрізків, на кожнім з яких знаходиться один і тільки один корінь заданого рівняння;
2) обчислення коренів з наперед заданою точністю. Перший етап називають ще задачею визначення відрізків ізоляції коренів, а другий – уточненням наближених коренів.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.57.173 (0.009 с.) |

 і
і  . Це обумовлює необхідність парної кількості відрізків:
. Це обумовлює необхідність парної кількості відрізків:
 ;
;
 . (3.8)
. (3.8)
 лінійна, формула Сімпсона є точною для многочленів до третього ступеня включно.
лінійна, формула Сімпсона є точною для многочленів до третього ступеня включно. за формулою Сімпсона,
за формулою Сімпсона,  .
.



 (3.9)
(3.9) , але і квадратурні коефіцієнти
, але і квадратурні коефіцієнти  .
. невідомих величин
невідомих величин  ,
,  визначаються за умови, що формула є точною у випадку будь-якого многочлена ступеня
визначаються за умови, що формула є точною у випадку будь-якого многочлена ступеня  .
. і
і  (
( ) наводяться у наступній таблиці:
) наводяться у наступній таблиці: )
)






















 слід провести заміну змінної
слід провести заміну змінної , (
, ( (3.11)
(3.11) .
. , використовуючи квадратурну формулу Гауса з чотирма ординатами.
, використовуючи квадратурну формулу Гауса з чотирма ординатами. ,
,  . Знаходимо інтеграл, що шукали, у вигляді
. Знаходимо інтеграл, що шукали, у вигляді ;
;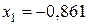 ;
; 
 ;
; 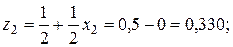
 ;
; 
 ;
; 






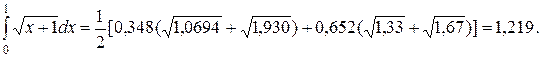
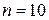 за формулами прямокутників, трапецій, Сімпсона, та з
за формулами прямокутників, трапецій, Сімпсона, та з 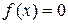 , (4.1)
, (4.1)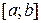 .
. , за яких рівняння (4.1) перетвориться в тотожність. Корінь рівняння (4.1) є нулем функції
, за яких рівняння (4.1) перетвориться в тотожність. Корінь рівняння (4.1) є нулем функції  і деяких трансцендентних функцій.
і деяких трансцендентних функцій. – точний корінь, а
– точний корінь, а 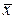 – його приблизне значення. Говорять, що корінь
– його приблизне значення. Говорять, що корінь 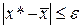 .
.


