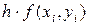Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбінований метод дотичних і хордСодержание книги
Поиск на нашем сайте
Характерна риса методів дотичних і хорд полягає в тому, що послідовності їхніх наближень монотонні. Причому, якщо для даного рівняння послідовність наближень методу хорд монотонно спадаюча, то послідовність наближень методу дотичних – монотонно зростаюча, і навпаки. Одночасне застосування цих методів дає можливість наближатися до кореня рівняння з двох сторін, одержуючи наближення з нестачею й надлишком.
Рисунок 4.4 – Геометрична інтерпретація комбінованого методу
Розглянемо рівняння У даному випадку за початкове наближення в методі хорд вибирають значення За значення кореня
Зауважимо, що на кожному кроці комбінованого методу за нерухомий кінець у формулі методу хорд потрібно брати наближення, обчислене на цьому ж кроці за формулою дотичних. Формули комбінованого методу дотичних і хорд наведені нижче:
За початкове наближення Завдяки своєрідній комбінації методів дотичних і хорд комбінований метод має більш високу швидкість збіжності, ніж методи хорд і дотичних окремо узяті.
Завдання на проведення лабораторної роботи Варіанти завдань представлені в таблиці 4.1. 1) Відокремити корені заданого рівняння 2) Уточнити один з відділених коренів рівняння двома, зазначеними в табл. 4.1, методами з точністю 3) Порівняти використані методи між собою за кількістю ітерацій, необхідних для знаходження кореня з заданою точністю. 4) Навести блок-схеми алгоритмів методів, які було використано в роботі.
Пояснення до виконання роботи. Виконуючи П.1 завдання, відрізок ізоляції кореня бажано звузити до довжини, що не перевищує одиниці. При уточненні ізольованого кореня методом ітерації наведене в табл. 4.1 рівняння необхідно привести до виду Перед тим як використовувати методи хорд, дотичних і комбінований, необхідно перевірити достатні умови збіжності відповідного методу.
Таблиця 4.1 – Варіанти завдань
Зміст звіту У звіті про лабораторну роботу необхідно навести: – Короткі теоретичні відомості; – Розв’язок завдань лабораторної роботи; – Аналіз результатів і висновки за лабораторною роботою.
4.4 Контрольні питання
– Достатні умови збіжності методу ітерації. – Умови існування й одиничності кореня. – Як вибрати початкове наближення при обчисленні кореня комбінованим методом.
Література
1. Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высш. шк., 1990. – 544 с. – C. 349 – 363. 2. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для вузов. – М.: Наука. Гл. ред. физ-мат. лит., 1989. – 432 с. – C. 190 - 195. 3. Численные методы. Н.Н. Калиткин. Главная редакция физико-математической литературы "Наука", М., 1978. – C. 138 – 146.
Лабораторна робота №5 Тема: Розв’язок звичайних диференціальних рівнянь першого порядку. Мета роботи: засвоєння на практиці чисельних методів розв’язку задачі Коші для звичайних диференціальних рівнянь першого порядку. Ідея: навчитися практично застосовувати методи розв’язку звичайних диференціальних рівнянь першого порядку, знати області їх застосування, переваги та недоліки кожного з методів. Теоретичні відомості Постановка задачі В залежності від кількості незалежних змінних диференціальні рівняння поділяються на дві групи: а) звичайні диференціальні рівняння, що містять одну незалежну змінну; б) рівняння з частинними похідними, які містять декілька незалежних змінних. Звичайні диференціальні рівняння містять, окрім незалежної змінної, одну або декілька похідних від функції, що шукається,
де Найвищий порядок
В ряді випадків із загального запису диференціального рівняння вдається виразити старшу похідну в певному виді. Наприклад,
Така форма запису називається рівнянням, розв’язаним відносно старшої похідної. Розв’язком диференціального рівняння називається будь-яка функція Загальний розв’язок звичайного диференціального рівняння
Частинний розв’язок диференціального рівняння можна отримати із загального, якщо довільним сталим надати певні значення. Для рівняння першого порядку загальний розв’язок залежить від однієї довільної сталої:
Якщо стала приймає певне значення
Виходячи з геометричної інтерпретації загального розв’язку диференціального рівняння першого порядку і із теореми Коші маємо, що для виділення деякого частинного розв’язку рівняння першого порядку достатньо задати координати Для диференціального рівняння другого порядку необхідно задати дві додаткові умови, завдяки яким можна визначити дві довільні сталі. В залежності від способу завдання додаткових умов для отримання частинного розв’язку диференціального рівняння, існує два різних типи задач: - задача Коші; - крайова задача. Додаткові умови в задачі Коші задають в одній точці Додаткові умови для крайової задачі задають в більш ніж одній точці, зазвичай в двох точках Методи розв’язку Методи розв’язку звичайних диференціальних рівнянь можна розбити на такі групи: графічні, аналітичні, наближені, числові. Графічні методи використовують геометричні побудови. Наприклад, метод ізоклін для розв’язку диференціального рівняння першого порядку виду (5.2), заснований на геометричному визначенні інтегральних кривих по заздалегідь побудованому полю напрямів, визначеному за ізоклінами. Аналітичні методи викладають в курсі диференціальних рівнянь. Вони дають можливість для ряду рівнянь першого порядку (з подільними змінними, лінійних, однорідних та ін.), а також для деяких типів рівнянь вищих порядків (лінійних зі сталими коефіцієнтами) отримати розв’язок в виді формул шляхом аналітичних перетворень. Наближені методи використовують різні спрощення самих рівнянь шляхом обґрунтованого відкидання деяких компонентів, що в них містяться, а також спеціальним вибором класів деяких функцій. Наприклад, в деяких інженерних задачах вдається представити розв’язок в виді суми двох складників, перший з яких визначає основний розв’язок, а другий – є малим доданком (збурення), квадратом якого можна знехтувати. На цьому засновані різні методи лінеаризації. Чисельні методи розв’язку диференціальних рівнянь на теперішній час є основним інструментом при дослідженні науково-технічних задач, що описуються диференціальними рівняннями. Найбільш розповсюдженим і універсальним методом розв’язку диференціальних рівнянь є метод кінцевих різниць. Він полягає у наступному. Область безперервної зміни аргументу заміняється дискретною множиною точок, які називають вузлами. Ці вузли складають різницеву сітку. Шукана функція безперервного аргументу наближено замінюється функцією дискретного аргументу на заданій сітці. Ця функція називається сітковою. Вихідне диференціальне рівняння замінюється різницевим рівнянням відносно сіткової функції. При цьому для похідних, які входять до рівняння, використовують відповідні кінцево-різницеві співвідношення. Наприклад, для обчислення похідної в точці
Отже, розв’язок диференціального рівняння зводиться до пошуку значень сіткової функції в вузлах сітки. Розглянемо застосування методу кінцевих різниць для розв’язку задачі Коші: знайти функцію, що задовольняє рівнянню:
та при
Розв’язок необхідно отримати для значень Згідно методу, здійснимо перехід від диференціальної задачі (5.4) відносно функції
Конкретний вираз правої частини рівняння (5.5) залежить від способу апроксимації похідної. Для кожного чисельного методу можна отримати свій вид рівняння (8.5). На основі аналізу виду різницевого рівняння (5.5) можна провести деяку класифікацію чисельних методів розв’язку задачі Коші для звичайних диференціальних рівнянь. Якщо в правій частині (5.5) відсутнє Якщо в праву частину рівняння (5.5) входить шукане значення
Метод Ейлера-Коші Метод Ейлера-Коші – найпростіший однокроковий метод першого порядку для числового інтегрування диференціальних рівнянь. Він реалізується такою рекурентною формулою:
де Похибка методу пропорційна Приклад 5.1 Розв’язати задачу Коші Рішення. Обчислення за формулою (5.6) наведемо в табліці:
□
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.141 (0.013 с.) |

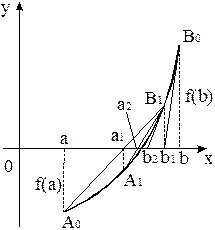
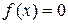 , корінь якого
, корінь якого 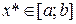 . Приймемо, наприклад,
. Приймемо, наприклад, 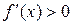 ,
, 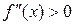 ,
,  ,
, 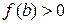 (рис. 4.4).
(рис. 4.4).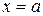 , а в методі дотичних – точку
, а в методі дотичних – точку  . На відрізку
. На відрізку 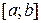 застосовують метод дотичних і хорд (спочатку дотичних, а потім хорд). У результаті одержують нові наближення
застосовують метод дотичних і хорд (спочатку дотичних, а потім хорд). У результаті одержують нові наближення  ,
,  , і початковий відрізок ізольованого кореня звужується. Для знаходження нових наближень застосовують метод дотичних і хорд уже на відрізку
, і початковий відрізок ізольованого кореня звужується. Для знаходження нових наближень застосовують метод дотичних і хорд уже на відрізку 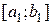 . У результаті одержують наближення
. У результаті одержують наближення 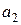 і
і 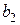 відповідно, причому
відповідно, причому 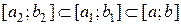 . Такий процес продовжують доти, поки довжина відрізка
. Такий процес продовжують доти, поки довжина відрізка 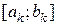 стане менше чи дорівнюватиме величині
стане менше чи дорівнюватиме величині 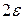 , де
, де 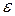 – наперед задана точність кореня.
– наперед задана точність кореня.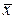 , який шукається, беруть напівсуму наближень
, який шукається, беруть напівсуму наближень  і
і  , тобто
, тобто  , а модуль їх напівсуми дає граничну абсолютну похибку наближеного кореня, тобто
, а модуль їх напівсуми дає граничну абсолютну похибку наближеного кореня, тобто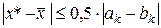 .
.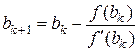 ,
, 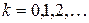 , (4.8)
, (4.8)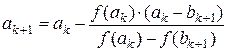 ,
, 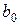 у формулі (4.8) методу дотичних беруть той з кінців відрізка
у формулі (4.8) методу дотичних беруть той з кінців відрізка  і її другої похідної мають однакові знаки, тоді протилежний кінець відрізка
і її другої похідної мають однакові знаки, тоді протилежний кінець відрізка 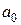 у формулі (4.9) методу хорд.
у формулі (4.9) методу хорд.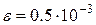 і
і  .
.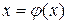 , де функція
, де функція 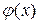 на відрізку ізоляції кореня повинна задовольняти умові
на відрізку ізоляції кореня повинна задовольняти умові  .
.
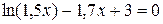
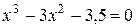
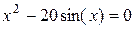
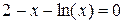
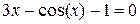
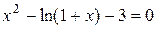

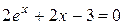
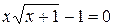

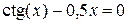


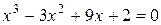
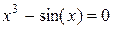

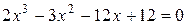

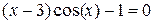

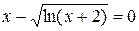
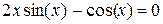
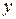 . Їх можна записати в виді:
. Їх можна записати в виді: , (5.1)
, (5.1)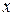 – незалежна змінна.
– незалежна змінна.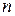 похідної, що входить в рівняння, називається порядком диференціального рівняння. Наприклад, загальний вид диференціальних рівнянь першого і другого порядків:
похідної, що входить в рівняння, називається порядком диференціального рівняння. Наприклад, загальний вид диференціальних рівнянь першого і другого порядків: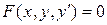 ,
, . (5.2)
. (5.2)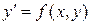 ,
,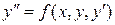 .
.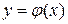 , яка, після підстановки її в рівняння, перетворює його на тотожність (вірну рівність).
, яка, після підстановки її в рівняння, перетворює його на тотожність (вірну рівність). , тобто загальний розв’язок має вид:
, тобто загальний розв’язок має вид: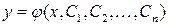 .
.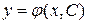 .
. , отримаємо частинний розв’язок:
, отримаємо частинний розв’язок: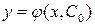 .
.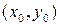 довільної точки на заданій інтегральній кривій.
довільної точки на заданій інтегральній кривій.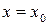 і називають початковими умовами, а точка, в якій їх задають – початковой точкой.
і називають початковими умовами, а точка, в якій їх задають – початковой точкой. та
та 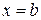 , які є границями області розв’язку диференціального рівняння, і називають граничними (крайовими) умовами.
, які є границями області розв’язку диференціального рівняння, і називають граничними (крайовими) умовами.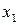 :
: ,
,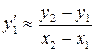 ,
,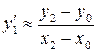 , (5.3)
, (5.3) .
.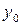 :
: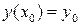 .
.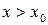 .
. ,
,  , попередньо ввівши послідовність точок
, попередньо ввівши послідовність точок 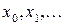 , кроки
, кроки 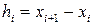 (
(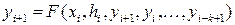 ,
,  , тобто значення
, тобто значення  попередніх значеннях
попередніх значеннях 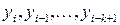 , то різницева схема називається явною. При цьому отримуємо
, то різницева схема називається явною. При цьому отримуємо  – однокроковий,
– однокроковий, 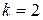 – двокроковий і т.д.
– двокроковий і т.д. (5.6)
(5.6)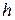 – крок прирощення змінної
– крок прирощення змінної 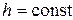 .
.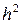 .
.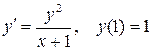 на відрізку
на відрізку 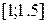 методом Ейлера-Коші з
методом Ейлера-Коші з 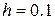 .
.