
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютна і відносна похибкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторна робота №1
Тема: Дії з наближеними величинами. Мета: отримання практичних навичок роботи з наближеними величинами, рішення прямої і зворотної задач теорії наближених обчислень. Ідея: систематизація правил і методів обчислювальної роботи над наближеними числами. Знати, в чому полягає основна задача теорії похибок і принцип рішення зворотної задачі теорії похибок.
Теоретичні відомості
Абсолютна і відносна похибки Наближеним числом Абсолютна похибка числа визначається:
де
Гранична абсолютна похибка наближеного числа
Значення точного числа
Якщо наближене число записано в десятковій системі счислення, то абсолютна похибка дорівнює одиниці останнього знаку, якщо число було отримано без округлення, і половині одиниці, якщо число було отримано з округленням. В даному випадку говорять відповідно про похибку в широкому і вузькому значенні. Відносною похибкою
Граничною відносною похибкою
і визначається виразом
Гранична відносна похибка часто виражається у відсотках
Приклад 1.1 Визначити граничну абсолютну похибку числа Рішення. Оскільки має місце нерівність:
Отже, можна прийняти Якщо врахувати, що
Десятковий запис наближених чисел. Значуща цифра числа. Кількість вірних знаків
Будь яке десяткове наближення число а може бути наведено у вигляді
де
Наприклад: Значущою цифрою наближеного числа називається будь яка цифра в його десятковому зображенні, відмінна від нуля, і нуль, якщо він міститься між значущими цифрами або є представником збереженого десяткового розряду.
Наближене число а вигляду (1.8) містить n вірних значущих цифр у вузькому значенні, якщо абсолютна похибка цього числа не перевершує половини одиниці десяткового розряду, що виражається n -й значущою цифрою, рахуючи зліва направо, тобто якщо виконується нерівність
Наближене число а вигляду (1.8) містить n вірних значущих цифр в широкому значенні, якщо абсолютна похибка цього числа не перевершує одиниці десяткового розряду, виразимого n -ю значущою цифрою, якщо рахувати зліва направо, тобто якщо виконується нерівність
Приклад 1.2 Округлити число 1,2500 до двох значущих цифр. Рішення. Отримаємо наближене число 1,2 з абсолютною похибкою, що дорівнює
Зв'язок між кількістю вірних значущих цифр і похибкою числа
Якщо строгий підрахунок похибок не робиться, то
Приклад 1.3 Зі скількома десятковими знаками треба узяти Рішення. Оскільки перша цифра 4, то
Пряма і зворотна задачі теорії похибок Пряма задача теорії похибок
Необхідно обчислити похибки даної функції, якщо відомі похибки аргументів. З теорії похибок відомо, якщо була задана функція, що диференціюється
де За граничну відносну похибка функції
Приклад 1.4 Знайти граничні абсолютну і відносну похибки об'єму кулі Рішення. Розглядаючи
Гранична абсолютна похибка об'єму:
Тому
Звідки гранична відносна похибка об'єму
Таблиця 1.1 – Варіанти значень до завдання 1
Завдання 2
1) Обчислити і визначити похибку результату (табл. 1.2). 2) Визначити, з якою абсолютною похибкою необхідно брати параметри, щоб відносна похибка результату не перевищувала 5% (табл.3).
Таблиця 1.2 – Варіанти значень до завдання 2.1
Таблиця 3 – Варіанти значень до завдання 2.2
Зміст звіту
У звіті з лабораторної роботи необхідно навести: – розрахункові формули; – розв’язок завдань за пунктом 1.2 методичних вказівок; – формулювання правил додання, віднімання і добутку наближених чисел; – аналіз отриманих результатів і висновки з роботи.
1.4 Контрольні питання.
1. Яке число називається наближеним? 2. Що називається похибкою наближеного числа? 3. Що таке абсолютна похибка? 4. Що таке гранична абсолютна похибка? 5. Що таке гранична відносна похибка? 6. Яка цифра наближеного числа називається вірною? 7. Як визначити абсолютну похибку наближеного числа по кількості його вірних цифр? 8. В чому полягає основна задача теорії похибок? 9. Чому дорівнюють гранична абсолютна і відносні похибки: суми, різниці, добутку, частинної похідної, ступеню, кореня? 10. Сформулюйте зворотну задачу теорії похибок. 11. В чому полягає принцип рівних впливів?
Література 1. Демидович Б.П, Марон И.А. Основы вычислительной математики. 3-е изд., испр. – М.: Наука, 1966. – 664 стр.
2. Краскевич В.Е., Зеленский К.Х., Гречко В.И. Численные методы инженерных исследований. – Киев: Высшая шк., 1986. – 263 стр. 3. Боглаев Ю.П. Вычислительная математика и программирование – М.: Высш. шк., 1990.-544 стр. Лабораторна робота №2 Тема: Інтерполяція функцій. Інтерполяційні формули Ньютона. Інтерполяційна формула Лагранжа. Мета: Скласти таблиці кінцевих різностей. Використовуючи інтерполяційну формулу, знайти значення функції в точці, що не є табличною, і оцінити похибку методу рішення; підібрати аналітичну формулу, що представляє з деякою точністю дані табличні значення функції. Вивчити метод побудови інтерполяційного полінома Лагранжа для довільно розташованих вузлів інтерполяції. Ідея: Вміти правильно складати таблиці кінцевих різностей. Навчитись грамотно застосовувати інтерполяційні формули в залежності від значень аргументів Теоретичні відомості 2.1.1 Кінцеві різниці n -х порядків Таблиці кінцевих різностей Розглянемо функцію Позначимо Тоді вираз
називається першою кінцевою різницею функції
Часто доводиться розглядати функції Кінцеві різниці послідовності
Кінцеві різниці n -х порядків зручно розташовувати у формі таблиць: горизонтальної (табл. 2.1) і діагональної (табл. 2.2).
Таблиця 2.1 – Горизонтальна таблиця різностей
Таблиця 2.2 – Діагональна таблиця різностей
Формула Лагранжа Розглянуті 1-а і 2-а інтерполяційні формули Ньютона придатні лише у випадку рівновіддалених вузлів інтерполяції. Для довільно заданих вузлів інтерполяції використовують інтерполяційну формулу Лагранжа. Побудуємо спочатку поліном
Аналогічно побудуємо поліном
І, нарешті, побудуємо поліном, що приймає в точках
Отримана формула (2.8) називається інтерполяційною формулою Лагранжа. Вона призначена для безпосередньої побудови інтерполяційного многочленна. Коефіцієнти Для обчислення коефіцієнтів Лагранжа може бути використана наведена нижче схема Ейткена. У таблиці
………………………………………………………………
Позначимо добуток елементів першого рядка через
Отже,
Похибка розрахунку має наступний вид:
де Для покращення наближення інтерполяційного полінома до функції Всі інтерполяційні формули виходять з інтерполяційної формули Лагранжа при відповідному виборі вузлів. Приклад 2.2. Для функції побудувати інтерполяційний поліном Лагранжа, вибравши вузли
Рішення. Обчислюємо відповідні значення функції:
Застосовуючи формулу (2.8), отримаємо:
або
Зміст звіту У звіті з лабораторної роботи необхідно навести: - короткі теоретичні відомості; - рішення завдань лабораторної роботи; - аналіз результатів і висновки по лабораторній роботі. 2.4 Контрольні питання 1. Мета і постановка задачі інтерполяції функції. 2. В чому полягає і як розв’язується задача інтерполяції? 3. Як побудувати інтерполяційний многочлен за 1-ою і 2-ю формулами Ньютона? 4. Як побудувати інтерполяційний поліном за формулою Лагранжа? 5. Які особливості інтерполяційної формули Лагранжа? 6. Як розраховуються коефіцієнти полінома Лагранжа у випадку рівновіддалених вузлів інтерполяції? 7. Як обчислити похибку інтерполяції деякої функції поліномом Лагранжа? Література 1. Демидович Б.П, Марон И.А. Основы вычислительной математики. 3-е изд., испр. – М.: Наука, 1966. – 664 стр. 2. Краскевич В.Е., Зеленский К.Х., Гречко В.И. Численные методы инженерных исследований. – Киев: Высшая шк., 1986. – 263 стр. 3. Боглаев Ю.П. Вычислительная математика и программирование – М.: Высш. шк., 1990. – 544 стр.
Тема: Чисельне інтегрування. Мета: Отримати практичні навики розв’язку задач чисельного інтегрування. Ідея: Навчитися складати квадратурні формули чисельного інтегрування. За допомогою різних формул обчислити інтеграл заданої функції та похибку. Порівняти між собою використані формули.
Загальні відомості Постановка задачі
Дана неперервна функція Якщо відома первісна
В багатьох практичних випадках первісна функція не може бути знайдена за допомогою елементарних засобів чи є занадто складною; крім того, на практиці підінтегральна функція часто задається таблицею. В цих випадках застосовують методи наближеного обчислення інтегралів.
Методи розв’язку задачі Звичайним прийомом чисельного обчислення інтеграла є заміна функції Замінюючи підінтегральну функцію будь-яким многочленом, отримуємо квадратурні формули типу
де
Кажуть, що, відкидаючи
де
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 4567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.50.163 (0.014 с.) |

 називається число, відмінне від точного і яке замінює останнє в обчисленнях.
називається число, відмінне від точного і яке замінює останнє в обчисленнях. (1.1)
(1.1) – точне значення числа;
– точне значення числа; (1.2)
(1.2) укладено в наступних межах:
укладено в наступних межах: або
або  (1.3)
(1.3) даного наближеного числа називається відношення абсолютної похибки цього числа до модуля відповідного точного числа, тобто
даного наближеного числа називається відношення абсолютної похибки цього числа до модуля відповідного точного числа, тобто (1.4)
(1.4) числа називається будь яке число, не менше відносної похибки цього числа.
числа називається будь яке число, не менше відносної похибки цього числа.  (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) , що замінює число
, що замінює число  .
. , то
, то 

 , то матимемо кращу оцінку:
, то матимемо кращу оцінку: 
 (1.8)
(1.8)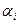 – цифра числа, причому
– цифра числа, причому 
 – старший десятковий розряд числа
– старший десятковий розряд числа  .
.
 (1.9)
(1.9) (1.10)
(1.10)
 можна приблизно оцінити за формулами
можна приблизно оцінити за формулами – у вузькому значенні (1.11)
– у вузькому значенні (1.11) – у широкому значенні. (1.12)
– у широкому значенні. (1.12) , щоб відносна похибка була рівною 0,1%?
, щоб відносна похибка була рівною 0,1%? , та
, та  . Маємо
. Маємо  , звідки
, звідки  і
і  .
. і дані
і дані  – абсолютні похибки аргументів, то з урахуванням виразу (1.2), гранична абсолютна похибка функції:
– абсолютні похибки аргументів, то з урахуванням виразу (1.2), гранична абсолютна похибка функції: (1.13)
(1.13) - граничні абсолютні похибки аргументів функції
- граничні абсолютні похибки аргументів функції  .
. можна прийняти:
можна прийняти: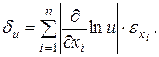 (1.14)
(1.14) , якщо діаметр
, якщо діаметр  см
см  см, а
см, а 
 і
і  як змінні величини, обчислюємо частинні похідні
як змінні величини, обчислюємо частинні похідні



 0.016
0.016








































 0.02
0.02











 і від величини
і від величини  , а також вміти оцінити похибку інтерполяційних формул Ньютона та Лагранжа. З’ясувати відмінність інтерполяційної формули Лагранжа від інтерполяційних формул Ньютона.
, а також вміти оцінити похибку інтерполяційних формул Ньютона та Лагранжа. З’ясувати відмінність інтерполяційної формули Лагранжа від інтерполяційних формул Ньютона. .
. – фіксовану величину збільшення аргументу (крок).
– фіксовану величину збільшення аргументу (крок). (2.1)
(2.1)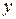 . Аналогічно визначаються кінцеві різниці вищих порядків:
. Аналогічно визначаються кінцеві різниці вищих порядків: кінцеві різниці вищих порядків.
кінцеві різниці вищих порядків. , задані табличними значеннями
, задані табличними значеннями  .
. визначаються співвідношеннями:
визначаються співвідношеннями:


















 , що приймає у точці
, що приймає у точці  значення
значення  , а у решті точок
, а у решті точок  значення
значення 
 .
. , що приймає у точці
, що приймає у точці  значення
значення  – значення
– значення  :
: . (2.7)
. (2.7) задані значення
задані значення  . Він буде дорівнювати сумі:
. Він буде дорівнювати сумі:

 . (2.8)
. (2.8) в цій формулі називаються коефіцієнтами Лагранжа.
в цій формулі називаються коефіцієнтами Лагранжа. розташовують таким чином:
розташовують таким чином:








 , другого через
, другого через  і т.д. (
і т.д. ( ), а добуток елементів головної діагоналі (елементи підкреслені) через
), а добуток елементів головної діагоналі (елементи підкреслені) через  . Звідки витікає, що
. Звідки витікає, що (2.9)
(2.9)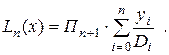
 , (2.10)
, (2.10) – значення інтерполяційного полінома Лагранжа у точці
– значення інтерполяційного полінома Лагранжа у точці 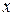 ,
,  – значення функції у точці
– значення функції у точці  ,
,  ,
,  .
. ,
,  ,
,  .
.

 Лабораторна робота №3
Лабораторна робота №3 . Розрахувати із заданою похибкою
. Розрахувати із заданою похибкою 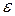 значення певного інтеграла від цієї функції на відрізку
значення певного інтеграла від цієї функції на відрізку  .
. заданої функції
заданої функції  (3.1)
(3.1)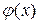 простого виду. Функція
простого виду. Функція  обчислювався безпосередньо.
обчислювався безпосередньо. (3.2)
(3.2)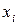 – обрані вузли інтерполяції;
– обрані вузли інтерполяції; – коефіцієнти, що залежать від вибору вузлів, але не від виду функцій;
– коефіцієнти, що залежать від вибору вузлів, але не від виду функцій;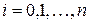 ;
; – залишковий член, який характеризує похибку квадратурної формули.
– залишковий член, який характеризує похибку квадратурної формули. , (3.3)
, (3.3) – значення інтегралу, обчисленого за допомогою формули наближеного інтегрування,
– значення інтегралу, обчисленого за допомогою формули наближеного інтегрування,  – точне значення інтегралу. Точним значенням інтегралу від заданої функції будемо вважати значення отримане за форму
– точне значення інтегралу. Точним значенням інтегралу від заданої функції будемо вважати значення отримане за форму 


