
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граничні похибки. Похибки функції.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Граничною (абсолютною чи відносною) похибкою називають найменшу можливу похибку наближення, яку можна отримати, виходячи з усіх відомих даних. Так, якщо відомо точне значення деякої величини Нехай Розглянемо задачу: визначити граничну абсолютну Δ(u) і граничну відносну δ(u) похибки наближення функції Звичайно f (х1 + Δх1, х2 + Δх2,…, хn + Δхn) = f (х1, х2, …, хn) + d f (х1, х2, …, хn) + r, (де d f (х1, х2, …, хn) = (Більш докладно: r – це сума доданків вигляду ô f ( Оскільки остання нерівність стає рівністю при умові ô f ( різниці між точним і наближеним значеннями функції у даній задачі не можна покращити. Отже, гранична абсолютна похибка Δ(u) дорівнює Δ(u) = Розділивши обидві частини нерівності (1) на ôuô = ô
Отже, відносною похибкою функції
Простими висновками з (1) і (2) є наступні твердження. 1. Гранична абсолютна похибка суми або різниці наближень дорівнює сумі їх граничних абсолютних похибок: Δ(a* 2. Гранична відносна похибка добутку або частки наближень приблизно дорівнює сумі їх граничних відносних похибок: δ(a* ∙ b*) = δ(a*/b*) ≈ δ(a*) + δ(b*) (при f (x1, x2) = x1 ∙ x2 або f (x1, x2) = x1 / x2). Звичайно, ці твердження можна отримати і безпосередньо. Наприклад, якщо а = а*(1
Похибки розв'язку. Похибка розв'язку задачі складається з 1) похибки математичної моделі, 2) неусувної похибки, 3) похибки методу і 4) обчислювальної похибки. Похибка математичної моделі пов'язана з тим, що звичайно модель описує явище наближено, з припущеннями і спрощеннями. Неусувна похибка зумовлена похибками у вхідних даних задачі. Похибка методу пов'язана з необхідністю для обчислення на комп’ютері наближено замінити неперервну модель дискретною або з неминучим обривом нескінченного процесу після скінченої кількості ітерацій. Похибку, яку дістають від заміни неперервної моделі дискретною, називають похибкою дискретизації (або похибкою апроксимації). Похибку, спричинену обривом ітераційного процесу, називають похибкою збіжності. Наприклад, якщо ми отримуємо числове значення sin x, обчислюючи його за допомогою ряду Тейлора Обчислювальні похибки – це похибки округлення чисел. Навіть якщо нема всіх інших вищезгаданих похибок, ця нехай вкрай мала погрішність є неминучою при обчисленнях. Річ в тім, що на комп’ютері операції виконують лише з певною кількістю значущих цифр, заданою його технічними характеристиками. У результаті виконання мільйонів операцій, кожна з яких вносить дуже маленьку похибку округлення, сумарна похибка принципово може значно перевищити результат обчислень. Проте величина таких похибок випадкова, вони мають різні знаки і компенсують одна одну. Як випливає з центральної граничної теореми теорії ймовірностей при N операціях математичне сподівання сумарної похибки приблизно дорівнює Систематичною причиною обчислювальних похибок є віднімання близьких за величиною чисел. Наприклад, розглянемо квадратне рівняння х2 – 140х + 1 = 0. Його корені х1,2 = 70
х2 = Тепер результат має 4 значущі цифри, точність значно вище. Річ в тім, що в перший раз було віднімання близьких за величиною чисел: при цьому зникають вірні значущі цифри. Втрата точності може статися і при додаванні до великих чисел відносно малих. Для спрощення у наступному прикладі будемо вважати, що всі числа мають 2 значущі цифри у десятковій системі числення, менші розряди відкидаються. Нехай а1 = 0,75, а2 = 0,024, а3 = 0,0072. Тоді а2 + а3 = 0,0312 ≈ 0,031, а1 + (а2 + а3) ≈ 0,78. З іншого боку а1 + а3 = 0,7572 ≈ 0,75, (а1 + а3) + а2 ≈ 0,75 + 0,024 = 0,774 ≈ 0,77. У другому випадку вірні цифри числа а3 були втрачені через те, що воно додавалося до надто великого для нього а1. Отже, взагалі для зменшення похибки додавати числа варто в порядку їх зростання. Зауважимо, що в даному прикладі наближення а1 + (а2 + а3) не дорівнює наближенню (а1 + а3) + а2 : у машинній арифметиці закони алгебри не завжди виконуються точно. Не можна ділити на числа близькі до нуля, бо навіть якщо абсолютна похибка Δа числа а дуже мала після ділення на близьке до нуля число b отримаємо велику абсолютну похибку Δа/ b числа а/ b. Дуже важливо при програмуванні обчислювальних алгоритмів уникати систематичних причин нагромадження похибок округлення: як бачимо на прикладах, ніщо тоді не гарантує малості сумарної обчислювальної похибки.
Стійкість і коректність. Означення 3. Задачу називають стійкою за вхідними даними з деякого класу, якщо її розв‘язок неперервно залежить від вхідних даних. Якщо ця умова не виконується, то задача вважається нестійкою за вхідними даними. Наприклад, задача інтегрування є стійкою на множині неперервних функцій на відрізку [a;b]. Дійсно, якщо Поняття стійкості характеризує чутливість задачі до неточностей у вхідних даних і безпосередньо пов’язано з методами обчислень. Якщо задача стійка, то достатньо малі похибки вхідних даних спричиняють й малі похибки розв‘язку задачі. Якщо ні, то як завгодно незначні похибки вхідних даних можуть призвести до як завгодно великих похибок розв’язку, тобто розв’язок може бути зовсім спотворений. Розглянемо це більш докладно на прикладі методу чисельного диференціювання. Нехай Може статися і так, що для розв‘язування стійкої за вхідними даними задачі використовується нестійкий метод обчислень. Наприклад, нехай треба знайти інтеграл
Інтегруючи за частинами, маємо
Звідси дістанемо
Використавши рекурентне співвідношення, обчислимо перші дев‘ять інтегралів
Значення інтеграла Цей приклад свідчить, що поняття стійкості та означення 3 доречно використовувати не тільки для задачі, але й для методу її розв‘язування. Введемо нарешті поняття коректності задачі. Означення 4. Задача називається коректно поставленою, якщо для будь-яких вхідних даних з деякого класу існує єдиний і стійкий за вхідними даними її розв‘язок. Наведена вище задача обчислення інтегралів є коректно поставленою на множині неперервних функцій, а диференціювання – некоректно поставленою задачею на множині диференційовних функцій. Як показано у прикладах, для розв‘язання некоректно поставлених задач безпосередньо застосовувати чисельні методи не варто, оскільки похибки округлень при розрахунках можуть катастрофічно зрости і призвести до результату, далекого від шуканого розв‘язку. Для розв‘язання некоректно поставлених задач використовують так звану регуляризацію: замінюють дану задачу коректно поставленою. Наприклад, для знаходження похідної функції Питання, тести 1. Методи обчислень – це алгоритми знаходження таких розв’язків математичних задач:
2. Оцінюючи якість (ефективність) методу, враховують такі його чинники:
3. Абсолютною похибкою наближення а* до точного значення а називають таку величину Δ(а*), для якої
4. Відносною похибкою (погрішністю) наближення а* до точного значення а називають таку величину δ(а*), що
5. Запис результату обчислень а = 1,123
6. Запис результату обчислень а = 1,123(1
7. У числа 0,00735000 значущих цифр всього
8. Якщо Δ(а*) = 0,0000003, то у числа 0,02076000 вірних значущих цифр всього
9. Якщо а = 1 ± 0,05, b = 0 ± 0,02, u = a2b, то
10. Якщо а = 3 ± 0,01, b = 2 ± 0,02, u = a – b, то
11. Якщо а = 4 ± 0,06, b = 2 ± 0,02, u = a/b, то
12. При обчисленнях з дійсними числами на комп’ютері неминучою є похибка
13. Нехай а1 = 3,4; а2 = 0,54; а3 = 0,037; а4 = 0,026. Похибка обчислень буде найменшою при такому порядку дій (всі числа мають дві вірні значущі цифри):
14. Нехай а1 = 4,726; а2 = 4,725; а3 = 2,132. Похибка обчислень буде найменшою при такому порядку дій (всі числа мають чотири вірні значущі цифри):
15. Ця задача є стійкою
16. Малі похибки вхідних даних спричиняють малі похибки розв‘язку такої задачі
17. Якщо задача є стійкою, то й метод її розв’язання є стійким
18. Ця задача є коректно поставленою
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.24 (0.014 с.) |

 , то абсолютною граничною похибкою його наближення х* є Δ(х*) =│
, то абсолютною граничною похибкою його наближення х* є Δ(х*) =│  – диференційовна функція, х1, х2, …, хn – наближення аргументів функції,
– диференційовна функція, х1, х2, …, хn – наближення аргументів функції,  = Δ(хi)
= Δ(хi)  – граничні абсолютні похибки наближень.
– граничні абсолютні похибки наближень. – дуже малі величини, будемо тут вважати їх достатньо малими для того, щоб у формулі Тейлора
– дуже малі величини, будемо тут вважати їх достатньо малими для того, щоб у формулі Тейлора ), залишковий член r – вищого порядку малості відносно Δхi – уже не впливав на вірні значущі цифри наближення f (х1, х2, …,хn).
), залишковий член r – вищого порядку малості відносно Δхi – уже не впливав на вірні значущі цифри наближення f (х1, х2, …,хn). ∙ ΔхiΔхj і якщо Δхi ~ 10-12, то ΔхiΔхj ~ 10-24). Нехай
∙ ΔхiΔхj і якщо Δхi ~ 10-12, то ΔхiΔхj ~ 10-24). Нехай  = х1 + α1Δх1,
= х1 + α1Δх1,  = х2 + α2Δх2, …,
= х2 + α2Δх2, …,  = хn + αnΔхn, де ôαiô£ 1 – це точні значення аргументів функції. Тоді
= хn + αnΔхn, де ôαiô£ 1 – це точні значення аргументів функції. Тоді
 , αi = 1 при кожному i = 1, 2, …, n, яка для деяких наближень х1, х2, …, хn фактично і здійснюється, то оцінку
, αi = 1 при кожному i = 1, 2, …, n, яка для деяких наближень х1, х2, …, хn фактично і здійснюється, то оцінку (1)
(1) .
. ô будемо мати
ô будемо мати
 (2)
(2) b*) = Δ(a*) + Δ(b*) (при f (x1, x2) = x1 ± x2).
b*) = Δ(a*) + Δ(b*) (при f (x1, x2) = x1 ± x2). (1
(1 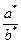 (1
(1  , то ми вимушені будемо обірвати процес обчислень на якомусь кроці k. Оскільки в даному випадку знаки ряду чергуються, то, як відомо, модуль наступного члена ряду
, то ми вимушені будемо обірвати процес обчислень на якомусь кроці k. Оскільки в даному випадку знаки ряду чергуються, то, як відомо, модуль наступного члена ряду  є абсолютною похибкою такого наближення, тобто похибкою збіжності.
є абсолютною похибкою такого наближення, тобто похибкою збіжності. , де ε – середня обчислювальна похибка одної операції. Якщо немає систематичних причин, то нагромадження похибок округлення незначне.
, де ε – середня обчислювальна похибка одної операції. Якщо немає систематичних причин, то нагромадження похибок округлення незначне. . Будемо вважати, що всі числа мають 4 значущі цифри у десятковій системі числення, менші розряди відкидаються. Після округлення отримуємо
. Будемо вважати, що всі числа мають 4 значущі цифри у десятковій системі числення, менші розряди відкидаються. Після округлення отримуємо  , менший корінь х2 = 70 – 69,99 = 0,0 1. Тут залишилась одна значуща цифра. Це ж саме х2 можна знайти, “позбувшись ірраціональності у чисельнику”:
, менший корінь х2 = 70 – 69,99 = 0,0 1. Тут залишилась одна значуща цифра. Це ж саме х2 можна знайти, “позбувшись ірраціональності у чисельнику”: 0,00 7142 85….
0,00 7142 85…. (x), g(x) – неперервні функції на [a;b] і
(x), g(x) – неперервні функції на [a;b] і  , то
, то  , тобто
, тобто  , якщо ε → 0. Навпаки задача диференціювання є нестійкою на множині диференційовних функцій на інтервалі (0;π). Дійсно, якщо
, якщо ε → 0. Навпаки задача диференціювання є нестійкою на множині диференційовних функцій на інтервалі (0;π). Дійсно, якщо  , гранична абсолютна похибка виразу
, гранична абсолютна похибка виразу  =
=  . Оскільки для наближення до
. Оскільки для наближення до  → ∞, то й виявляється, що як завгодно незначна обчислювальна похибка Е може призвести до як завгодно великих похибок розв’язку.
→ ∞, то й виявляється, що як завгодно незначна обчислювальна похибка Е може призвести до як завгодно великих похибок розв’язку.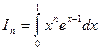 ,
, 

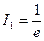 ,
,  ,...,
,...,  .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
, ,
,  ,
,  .
. помилкове, оскільки підінтегральна функція
помилкове, оскільки підінтегральна функція  в усіх точках відрізка
в усіх точках відрізка  невід‘ємна. Помилка зумовлена похибкою округлення значення
невід‘ємна. Помилка зумовлена похибкою округлення значення  до шести значущих цифр. Ця похибка наближено дорівнює
до шести значущих цифр. Ця похибка наближено дорівнює  . Але при обчисленні
. Але при обчисленні  вона множиться на – 2,
вона множиться на – 2,  на (– 2) ∙ (– 3) і т.д. Похибка в
на (– 2) ∙ (– 3) і т.д. Похибка в  . Вона спотворила істинне значення
. Вона спотворила істинне значення  з невідомою функцією g(x). Така задача вже коректна завдяки стійкості задачі інтегрування, отже вона є регуляризацією задачі диференціювання.
з невідомою функцією g(x). Така задача вже коректна завдяки стійкості задачі інтегрування, отже вона є регуляризацією задачі диференціювання.




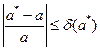
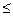 а
а 


