
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Похибки та запис експериментального результатуСодержание книги
Поиск на нашем сайте
Вимірювати те, що вимірю-ване, робити виміряним те, що ще не виміряне. Галілео Галілей Досвід роботи з учнями, слухачами підготовчих відділень та курсів, студентами вузів вказує на низку некоректних ходів, нерозуміння ними певних моментів і, що найгірше, неправильного застосування певних прийомів, методів оцінки похибок під час обробки експериментальних результатів. Їх можна звести до таких трьох проблем: 1) шаблонне, несвідоме застосування статистичного методу знаходження середнього значення і середнього відхилення до абсолютно усіх результатів як вимірювання, так і визначення значення будь-якої фізичної величини: 2) практично повне нерозуміння, невміння (деякими вчителями та викладачами в тому числі) визначати абсолютні похибки фізичних величин в процесі їх прямого виміру; 3) невміння записувати результати прямих вимірів і кінцеве значення шуканої величини з відповідною кількістю значущих цифр. Така низька культура оформлення результатів експериментальних досліджень є результатом, по-перше, неглибокого, поверхового проникнення в саму суть явища чи процесу, які досліджуються, а, по-друге, надмірного захоплення „математичним татуюванням”, – таким характерним для псевдонауки. Фізика – наука точна. Тому будь-яке фізичне явище можна вважати зрозумілим тільки в тому випадку, якщо його вдалось описати точною мовою законів, формул і чисел. Але для того, щоб виразити фізичну величину чисельно, її необхідно виміряти або визначити за допомогою інших величин, які вимірюються безпосередньо. Щоб справитися з цими проблемами, треба глибше вникнути у фізичну суть самого процесу виміру, тобто співставлення „чогось” з „чимось”. Оте "щось" визначає філософський аспект його виміру, а оте „чимось” і саме співставлення – методичний. Філософський аспект виміру спричинений двома особливостями. Перша стосується принципів світобудови, а друга – наших (земної людини) співвідносин із об’єктами, проявами цього всесвіту. Перша особливість: Сучасна фізика – це польова фізика, вона дає відповіді про першопричини багатьох явищ та процесів на польовому рівні. Адже мікрочастинки, поведінка яких визначає хід процесів та явищ, є польовими утвореннями. Тобто вони не мають „кінця”, відповідно не мають ні „кінця” ні „початку” будь-які предмети, об’єкти всесвіту, розміри яких ми вимірюємо. А якщо ще пригадати принцип невизначеності Гейзенберга, його застосування до енергії та часу... Іможе аж тоді стане зрозумілою фраза давньогрецького мудреця Зенона, що „вірити можна тільки розуму”. Схоже він мав рацію, заперечуючи можливість абсолютного пізнання світу за допомогою наших чуттів. Друга особливість: Практично ніколи ми не можемо виміряти те, що нам треба виміряти. Тому ми міряємо те, що можемо виміряти, і стараємось, щоб те. що ми міряємо, якнайточніше, якнайближче відповідало тому, що нам треба виміряти. А степінь отої відповідності треба навчитись (привикнути) оцінювати. Тому, приступаючи до вимірювання значення будь-якої фізичної величини, необхідно пам’ятати, що: ● експериментатор має справу з реальними конкретними речами, предметами, а не з моделями, а наш понятійний апарат базується на теоретичних засадах, тобто зорієнтований на моделі, а не на реалії; ● перед проведенням вимірів необхідно усвідомити суть тої о. що беремося виміряти; для правильного аналізу і виміру значення будь-якої фізичної величини треба підходити функціонально,– тобто вияснити, чим є дана річ чи величина, яку функцію вона виконує. Для одержання експериментального значення будь-якої величини необхідно придумати спосіб, метод її визначення; підібрати відповідне обладнання та інструмент, які б забезпечили максимально більшу точність її визначення. Для досягнення поставленої мети потрібно виконати цілу низку взаємопов’язаних етапів. Перший з них – це прямі виміри тих величин, за допомогою яких будемо в подальшому визначати значення шуканої величини. Це – найважливіший і найвідповідальніший етап, який визначає ефективність, точність і доцільність всієї подальшої роботи, тобто наступних етапів, які, по суті, є обробкою отриманих результатів прямих вимірів. Особливу увагу слід звертати при цьому на точність вимірювання значень різних величин. Абсолютна похибка прямих вимірів має, як мінімум, три джерела. Тому для її оцінки, визначення потрібно провести копітку роботу. Перше, на що слід звернути увагу; – це аналіз об’єкту вимірювання. Тобто треба чітко усвідомити, побачити, – що ми міряємо? Причому аналіз об’єкту повинен бути функціональний. Тобто треба зрозуміти, яку функцію об’єкт виконує, і тільки тоді стане зрозуміло – що ж саме ми міряємо. Наприклад, для визначення довжини хвилі падаючого на дифракційну решітку світла потрібно виміряти відстань від лампочки до решітки. Тобто об’єктом виміру є ця відстань. Але ж це не проста відстань між якимись „точками”. Лампочка є джерелом світла, яке взаємодіє з дифракційною решіткою. Це означає, що нас цікавить шлях світла, яке „народжується” атомами спіралі. А спіраль (нитка розжарення) для кожного джерела світла має свою форму, просторову орієнтацію, протяжність. Тобто шлях світлового потоку починається не з деякої точки, а з певної смуги невизначеності, яка в даному випадку визначається конфігурацією спіралі лампочки. Половину ширини цієї смуги невизначеності Δ l/2 треба врахувати в тій частині абсолютної похибки, яка визначається об’єктом, – Δ l1. Так само слід поступити і при аналізі завершення шляху променів, – їх взаємодія із дифракційною решіткою також має деяку просторову протяжність Δ l2. Тобто кінцево отримуємо: Δ lо = l/ 2(Δ l1 + Δ l2). Друге джерело – це інструмент, з яким співвідноситься об’єкт, Δ lі – частина абсолютної похибки прямого виміру, спричинена точністю інструменту, який використовується. Третє джерело – це сам спосіб, метод виміру. Наявність доступу до об’єкта, паралельність інструмента та об’єкта, впливи різних полів і т.і., – все це може вплинути на точність виміру і вплив цих факторів треба навчитись контролювати через Δ lс – частину абсолютної похибки, спричинену способом вимірювання. Тобто результуюче значення абсолютної похибки регулярно включає в себе згадані складові: Δ l = Δ lо + Δ lі + Δ lс. Вони можуть бути різними. В кожному конкретному випадку може домінувати то одна, то друга, то третя. Прийнято розрізняти три види похибок: промахи, систематичні і випадкові похибки вимірювання. Промахи (прорахунки) є результатом низької кваліфікації експериментатора, що виконував виміри. Промахи не піддаються обліку. Систематичні похибки є наслідком недосконалості приладів, а також недоліків методики виміру. Вони завжди дають відхилення результату виміру від дійсного значення в одну і ту ж сторону. Долаються систематичні похибки шляхом перевірки приладів, повнішої розробки теорії і методики експерименту і порівняння різних методів виміру однієї і тієї ж величини. Якщо систематичні похибки, що виникають під час вимірювання яким-небудь приладом, значно менші, ніж поділки шкали цього приладу, то за абсолютну похибку виміру зазвичай беруть половину найменшої поділки приладу. Коли говорять про інструментальні похибки, то мають на увазі похибки, залежні від похибок вживаних засобів вимірів. Останні у свою чергу характеризуються класом точності приладу. Клас точності визначається максимальною похибкою приладу, вираженою у відсотках від повної величини шкали. Наприклад, клас точності 0,5 означає похибку приладу до 0,5% за відхилення стрілки на всю шкалу. При відхиленні стрілки на половину шкали похибка зростає в два рази, а на третину шкали – в три рази, і так далі. Тому для вимірів з меншою похибкою треба вибирати прилад такої чутливості, щоб вимірювана величина викликала відхилення стрілки приладу більш ніж на половину шкали. Величина інструментальної похибки визначається порівнянням показів даного і еталонного приладів. Надійність показів еталонного приладу розраховується з врахуванням випадкових похибок. Випадкові похибки є наслідком випадкових, неконтрольованих перешкод, вплив яких на процес виміру неможливо врахувати безпосередньо. Цих перешкод дуже багато, вони різної фізичної природи і відрізняються силою дії на процес виміру. Можна вживати заходи для усунення найбільш впливових перешкод, але повністю їх усунути неможливо. Випадкові похибки можуть відхиляти результати виміру від дійсного значення в обидві сторони, і їх вплив враховується за допомогою певної обробки результатів виміру фізичної величини. Вищенаведені особливості є причиною того, що доводиться розрізняти істинне та дійсне значення фізичної величини. Істинне значення фізичної величини – це таке значення величини, яке ідеальним чином відобразило б в якісному та кількісному відношеннях відповідну властивість об’єкта. Дійсне значення фізичної величини – це таке значення величини, яке знаходять експериментально. Воно настільки наближається до істинного, наскільки це дозволяють умови експерименту, вимірювальна техніка, технічна культура самого експериментатора, нарешті. Для даної цілі воно може бути використаним замість істинного значення. Виміром якраз і називають знаходження дійсного значення даної фізичної величини дослідним шляхом із використанням спеціальних технічних засобів - інструментів та установок. Теорія похибок враховує тільки випадкові похибки. Згідно цієї теорії, випадкові похибки вимірів підкоряються закону нормального розподілу (закону Гауса). Сенс цього закону полягає в наступному. Припустимо, ми хочемо виміряти деяку фізичну величину, дійсне (і нам невідоме) значення якої є
Тут х o–позначений набір значень, які ми отримуємо в результаті вимірювання,
Як видно з рисунку, гаусова крива, що має на графіку симетричний (як дзвін) вигляд, характеризується двома параметрами: положенням вершини – Обробка результатів серії вимірів зводиться до точнішого знаходження параметрів гаусовї кривої Оскільки немає сенсу прагнути до дуже великої кількості вимірювань, то виникає питання: як змінюється достовірність залежно від числа вимірювань? Залежність ця складна і не виражається в елементарних функціях. Існують спеціальні таблиці (таблиці коефіцієнтів Ст’юдента), за якими можна визначити, в скільки разів треба збільшити стандартний довірчий інтервал
тут Хід обробки результатів вимірювань має бути наступним: виконавши n вимірювань і записавши їх результати в таблицю, обчислюють за (3) середнє арифметичне значення вимірюваної величини
що означає, що дійсне значення вимірюваної величини Мірою точності результатів вимірювань є відносна похибка, виражена у відсотках:
Зворотна до неї величина Точність обробки результатів вимірювань повинна узгоджуватися з точністю самих вимірювань. Обчислення, проведені з більшим, ніж необхідно, числом десяткових знаків, вимагають зайвої витрати сил. Треба дотримуватися правила: похибка обчислень має бути на порядок меншою від похибки вимірювання. Наведена методика обробки результатів вимірювань відноситься до прямих вимірювань. У випадках непрямих вимірів, коли числове значення вимірюваної величини знаходиться за формулою, що пов’язує її з величинами, знайденими з прямих вимірів, похибка непрямого вимірювання знаходиться за допомогою похибок прямих вимірів за правилом диференціювання:
Так, наприклад, похибка під час вимірювання прискорення вільного падіння за виміром періоду
Передбачається, що похибки незалежних вимірювань (тут На практиці для обчислення похибок непрямих вимірювань зручніше відразу обчислювати відносну похибку за правилом диференціювання натурального логарифма функції. Наприклад,
Похибки незалежних вимірювань вважають грубими або неістотними залежно від того, вносять вони помітний вклад в похибку остаточного результату чи ні. Неістотні похибки достатньо оцінювати приблизно, але обов’язково із завищенням. Запис дійсного значення: ■ Дійсне значення записується за допомогою певної кількості значущих цифр. ■ Воно ніколи не є точкою на відповідній осі, а завжди є інтервалом, всередині якого і знаходиться істинне значення даної фізичної величини. ■ Ширина цього інтервалу оберненою залежністю пов’язана із кількістю значущих цифр. Тобто чим точніше ми визначаємо або вимірюємо дійсне значення деякої фізичної величини, чим вужчим є інтервал невизначеності (подвоєна абсолютна похибка), тим більша кількість значущих цифр використовується для його написання. Наприклад: Нехай відносна похибка ε дорівнює 0,1 або 10%, а експериментальне значення (покази калькулятора) – А = 0,00347291 або 3,47291 ∙ 10-3. Першим кроком є визначення кількості значущих цифр за значенням відносної похибки. Це означає, що кількість значущих цифр для ε = 0,1 не повинна перевищувати два розряди, тобто тільки одна цифра 3 є точною, друга потребує уточнення – це 4, а всі наступні – є незначущими. Тобто експериментальне значення необхідно записати так: 0,0035 (заокругливши 47 до 50) або 3,5 ∙ 10-3. Другим кроком є уточнення (корекція) другої цифри. Для цього визначається абсолютна похибка Δ = А ∙ε: 0,00347 ∙ 0,1 = 0,00035 (береться одну або максимум дві цифри!). Отримане значення визначає ширину довірчого інтервалу експериментального значення: 0,0035 ± 0,0003 або 0,00347 ± 0,00035. Якщо ж ε = 0.01, то експериментальне значення записується у вигляді: 0,00347 ± 0,00003 або 0,003473 ± 0,000035 (дві значущі цифри і третя 7 з корекцією ± 3). Якщо ж ε = 0.001, то експериментальне значення записується у вигляді: 0,003473 ± 0,000003 або 0,0034729 ± 0,0000035 (три значущі цифри і четверта 3 (заокруглена) з корекцією ± 3).
Особливість визначення абсолютних похибок в процесі виконання віртуальних лабораторних робіт: Зміна значень певних фізичних параметрів у вікні інтерфейсу комп’ютерної програми відбувається дискретно, тобто з певним кроком. Тоді за абсолютну похибку значення даного параметру береться половинка цього кроку. Наприклад, швидкість потоку υ = 14,1 м/с, з кроком0,1 м/с, тоді Δ υ = 0,05 м/с; циклічна частота ω = 8,5 с-1 з кроком 0,5 с-1, тоді Δ ω = 0,25 с-1. Якщо ж значення параметрів чи фізичних сталих беруться з певною кількістю знаків (розрядів), то абсолютна похибка береться як половинка першого вільного розряду. Наприклад, І = 15,4 мА, тоді ΔІ = 0.05 мА; π = 3,14, тоді Δπ = 0,005; NA = 6,02∙1023, тоді ΔNA = 0,005∙1023.
МЕХАНІКА В-10 Вивчення законів руху рідин та газівМета: вивчити основні закономірності руху рідини та газу (перевірка рівнянь нерозривності та Бернуллі). Прилади і матеріали: труба змінного перерізу, вентилятор, анемометри (2 шт.), манометричні трубки (2 шт.), масштабна лінійка. Теоретичні відомості Рух рідини називається течією, а сукупність частинок рідини, що рухається – потоком. Графічно рух рідин зображається за допомогою ліній струму, які проводяться так, що дотичні до них співпадають за напрямом з вектором швидкості рідини в даний момент часу. Лінії струму проводяться так, щоб густина їх була більша там, де більша швидкість руху рідини, і менша там, де рідина тече повільніше. Частина рідини, обмежена лініями струму, називається трубкою струму (рисунок10.1). Якщо поле швидкостей і відповідні йому лінії струму не міняються з часом, то рух рідини називається стаціонарним або сталим.
Рисунок 10.1 Розглянемо випадок ідеальної рідини [1]. Візьмемо довільну трубку струму. Оскільки швидкості частинок рідини напрямлені по дотичних до ліній струму, то при течії рідина не може перетинати бічну поверхню трубки струму. Трубка струму поводиться подібно бічній поверхні жорсткої трубки, уздовж якої тече рідина. Якщо поперечний переріз трубки струму нескінченно малий, то можна вважати, що швидкість рідини одна і та ж у всіх точках одного і того ж поперечного перетину і напрямлена уздовж осі трубки струму. Маса рідини, що протікає за час
де У випадку стаціонарної течії маса
Якби ця рівність не виконувалась, маса рідини між перерізами
Ця робота рівна приросту
знаходимо
Отже,
– рівняння Бернуллі (1700-1782). Рівняння Бернуллі виражає закон збереження механічної енергії для стаціонарного руху нестислої ідеальної рідини в однорідному полі сил тяжіння. З рівняння Бернуллі та рівняння нерозривності слідує, що при течії рідини по трубі, яка має різні перерізи, швидкість рідини більша у місцях звуження, а статичний тиск більший в більш широких місцях. Для горизонтально розташованої трубки (для якої
У рівнянні (10.6) тиск
За допомогою трубки Прандтля визначають динамічний напір Залежність тиску в рідині від величини її швидкості лежить в основі дії багатьох технічних пристроїв. Оскільки сума тиску і динамічного напору в потоці рідини стала, то в струмені тиск завжди менший, ніж у нерухомій рідині. При великих швидкостях тиск може стати меншим від атмосферного. Рідина, що протікає через вузьку частину трубки, перебуває в стані всебічного розтягу. Це явище застосовується в пульверизаторах, карбюраторах, водоструминних насосахта в інших приладах. На рисунку 10.4 наведено найпростіший пульверизатор.
Розглянемо течію ідеальної нестискуваної рідини через малий отвір в бічній стінці або дні широкої посудини. Всі лінії струму проходять через трубку, починаючись поблизу вільної поверхні рідини, де швидкість
де
Це — формула Торiчеллi (1608–1647). Вона показує, що при витiканнi рiдина отримує таку швидкiсть, яку отримало б тiло, що вiльно падає з висоти h. Тому, якщо зiгнути трубку i направити струю вертикально вгору або пiд малим кутом до вертикалi, то в щонайвищiй своїй точцi вона досягне рiвня рiдини в посудинi. Насправдi висота пiдняття струменя буде дещо менша через тертя i опiр повiтря, якi при отриманнi рiвняння Бернуллi не враховувалися. В реальних рідинах значення швидкості буде дещо менше, особливо якщо їх в’язкість значна, а отвір має необтічну форму. Коефіцієнт, який характеризує форму отвору, називається коефіцієнтом витікання μ (рисунок 10.6). Тоді формулу Торічеллі для визначення величини швидкості витікання рідини з отвору записують у вигляді:  При турбулентній течії середня швидкість по всьому поперечному перерізі потоку майже постійна. У пограничному тонкому шарі рідини, що прилягає до самих стінок труби, швидкість зменшується до нуля. Незважаючи на те що турбулентний потік за своїм змістом нестаціонарний, на практиці його умовно розглядають як стаціонарний потік з усередненими характеристиками. Кількісно перехід між режимами (ламінарним і турбулентним) характеризується числом Рейнольдса:  ,де ,де 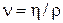 – кінематична в‘язкість, – кінематична в‘язкість,  – характерна швидкість потоку, – характерна швидкість потоку,  – характеристичний розмір. – характеристичний розмір. Величина числа Рейнольдса – порядку відношення кінетичної енергії рідини, що переноситься потоком через заданий переріз за одиницю часу, до величини роботи проти сил в‘язкого тертя, що виконується потоком також за одиницю часу. Отже, число Рейнольдса має порядок величини, яка визначається відношенням кінетичної енергії рідини до втрат енергії, зумовленої роботою сил в'язкості на шляху, що дорівнює характеристичній довжині. Число Рейнольдса визначає відносну роль інерції і в'язкості рідини під час течії. При великих числах Рейнольдса основну роль відіграє інерція, а при малих — в'язкість. Із збільшенням швидкості течії ламінарний рух переходить у турбулентний. Швидкість, при якій відбувається цей перехід, називають критичною. Замість критичної швидкості користуються числом Рейнольдса. Так, якщо за характерний розмір взяти радіус труби, то критичне значення числа Рейнольдса, при якому ламінарний рух переходить у турбулентний,  з'являється на табло. Натисканням кнопки "Стоп" екс з'являється на табло. Натисканням кнопки "Стоп" екс
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.64 (0.019 с.) |

 . Використовуючи який-небудь прилад, ми n разів намагаємося визначити цю величину, але через випадкові похибки, що виникають в процесі вимірювання, замість
. Використовуючи який-небудь прилад, ми n разів намагаємося визначити цю величину, але через випадкові похибки, що виникають в процесі вимірювання, замість  отримуємо набір значень
отримуємо набір значень  . Виявляється, що за допомогою закону розподілу ми хоча і не можемо вказати точне значення
. Виявляється, що за допомогою закону розподілу ми хоча і не можемо вказати точне значення  (область значень
(область значень  (1)
(1) і дорівнює
і дорівнює .(2)
.(2) – їх середнє арифметичне, а
– їх середнє арифметичне, а  – середнє квадратичне відхилення:
– середнє квадратичне відхилення: , (3)
, (3) . (4)
. (4) і „шириною”
і „шириною” 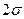 – відстанню між точками перегину. Значення
– відстанню між точками перегину. Значення  , як правило, і приймають за ту величину, яку треба було виміряти, а
, як правило, і приймають за ту величину, яку треба було виміряти, а  – 0,997). Міра
– 0,997). Міра  визначається фізичною суттю вимірюваної величини, а також фізичними і конструктивними принципами, закладеними в методику вимірювання. Ці принципи в рамках даної методики не залежать від експериментатора, отже, нескінченне збільшення кількості вимірів не дає помітного збільшення точності.
визначається фізичною суттю вимірюваної величини, а також фізичними і конструктивними принципами, закладеними в методику вимірювання. Ці принципи в рамках даної методики не залежать від експериментатора, отже, нескінченне збільшення кількості вимірів не дає помітного збільшення точності. , що за певної кількості вимірювань n отримати необхідну ймовірність
, що за певної кількості вимірювань n отримати необхідну ймовірність  . За стандартний береться довірчий інтервал
. За стандартний береться довірчий інтервал  . (5)
. (5)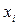 – числове значення величини, отримане при i-му вимірюванні,
– числове значення величини, отримане при i-му вимірюванні,  – середнє арифметичне значення вимірюваної величини (3).
– середнє арифметичне значення вимірюваної величини (3). і знаходять за таблицею коефіцієнт Ст’юдента
і знаходять за таблицею коефіцієнт Ст’юдента  , залежно від необхідної ймовірності
, залежно від необхідної ймовірності  ,
, знаходиться в інтервалі
знаходиться в інтервалі 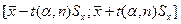 з ймовірністю
з ймовірністю  .
. називається точністю.
називається точністю. .
. коливань і довжини
коливань і довжини  математичного маятника визначається диференціюванням залежності
математичного маятника визначається диференціюванням залежності 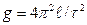 , тобто
, тобто .
.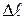 і
і  ) підсилюють одна одну і тому їх вплив враховується у формулі із знаком плюс.
) підсилюють одна одну і тому їх вплив враховується у формулі із знаком плюс. .
.
 через поперечний переріз трубки, визначається виразом
через поперечний переріз трубки, визначається виразом (10.1)
(10.1)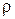 – густина рідини,
– густина рідини,  – площа (нормального) поперечного перерізу трубки.
– площа (нормального) поперечного перерізу трубки. буде однією і тією ж для всіх перерізів трубки струму. Якщо взяти два перерізи, площі котрих рівні
буде однією і тією ж для всіх перерізів трубки струму. Якщо взяти два перерізи, площі котрих рівні  i
i  , то можна записати
, то можна записати (10.2)
(10.2) , і співвідношення (10.2) приймає вигляд
, і співвідношення (10.2) приймає вигляд (10.3)
(10.3)
 (рисунок 10.2). Нехай ця частина перемістилася в нескінченно близьке положення
(рисунок 10.2). Нехай ця частина перемістилася в нескінченно близьке положення  . Обчислимо роботу
. Обчислимо роботу 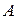 , виконувану при цьому силами тиску. Тиск, що діє на бічну поверхню трубки струму, перпендикулярний до переміщення і роботи не виконує. При переміщенні межі
, виконувану при цьому силами тиску. Тиск, що діє на бічну поверхню трубки струму, перпендикулярний до переміщення і роботи не виконує. При переміщенні межі  в положення
в положення  виконується робота
виконується робота  , де
, де  — величина переміщення.
— величина переміщення.  ,
,  або
або  , де
, де  —маса рідини в об’ємі
—маса рідини в об’ємі 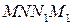 . При переміщенні межі
. При переміщенні межі  в положення
в положення  рідина виконує роботу проти сил тиску
рідина виконує роботу проти сил тиску  (або тиск
(або тиск  де
де  —маса рідини в об’ємі
—маса рідини в об’ємі  . Але якщо рух стаціонарний, то маса рідини в об’ємі
. Але якщо рух стаціонарний, то маса рідини в об’ємі  не зміниться, а тому із закону збереження маси отримаємо
не зміниться, а тому із закону збереження маси отримаємо  . Остаточно знаходимо, що
. Остаточно знаходимо, що
 повної енергії виділеної частини рідини. Зважаючи на стаціонарність течії, енергія рідини в об’ємі
повної енергії виділеної частини рідини. Зважаючи на стаціонарність течії, енергія рідини в об’ємі 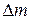 в положеннях
в положеннях 
 . Прирівнюючи цю величину до роботи
. Прирівнюючи цю величину до роботи  , отримаємо
, отримаємо (10.4)
(10.4) (10.5)
(10.5) ) закон Бернуллі має вигляд:
) закон Бернуллі має вигляд: (1.6)
(1.6) називають статичним. Його вимірюють за допомогою манометричних трубок з перерізом, паралельним лінії течії. Для вимірювання складової тиску, зумовленого рухом рідини
називають статичним. Його вимірюють за допомогою манометричних трубок з перерізом, паралельним лінії течії. Для вимірювання складової тиску, зумовленого рухом рідини  , застосовують трубки з перерізом, перпендикулярним до лінії течії. Цю складову називають динамічним тиском, а суму
, застосовують трубки з перерізом, перпендикулярним до лінії течії. Цю складову називають динамічним тиском, а суму  називають повним тиском, або повним напором. Для його вимірювання користуються трубкою Піто. Вона являє собою зігнуту манометричну трубку, яку розташовують у рухомій рідині так, що її відкритий кінець повернутий назустріч течії рідини (рисунок 10.3, а). Для вимірювання статичного тиску р користуються зондом. Він відрізняється від трубки Піто тим, що його передня частина, яка повернута назустріч потоку рідини, запаяна, а в боковій стінці є невеликий отвір (рисунок 10.3, б). На практиці трубку Піто і зонд суміщають в одному приладі, який називають трубкою Прандтля (рисунок 10.3, в). Трубка Піто порушує характер руху рідини, і безпосередньо перед вхідним отвором виникає область, в якій швидкість руху частинок рідини зменшується до нуля (
називають повним тиском, або повним напором. Для його вимірювання користуються трубкою Піто. Вона являє собою зігнуту манометричну трубку, яку розташовують у рухомій рідині так, що її відкритий кінець повернутий назустріч течії рідини (рисунок 10.3, а). Для вимірювання статичного тиску р користуються зондом. Він відрізняється від трубки Піто тим, що його передня частина, яка повернута назустріч потоку рідини, запаяна, а в боковій стінці є невеликий отвір (рисунок 10.3, б). На практиці трубку Піто і зонд суміщають в одному приладі, який називають трубкою Прандтля (рисунок 10.3, в). Трубка Піто порушує характер руху рідини, і безпосередньо перед вхідним отвором виникає область, в якій швидкість руху частинок рідини зменшується до нуля ( ). Тоді з рівняння (10.6) дістаємо
). Тоді з рівняння (10.6) дістаємо .
. .
.
 зневажливо мала (ми вважаємо, що площа отвору набагато менша за площу вільної поверхні). Застосуємо рівняння Бернуллі до точок
зневажливо мала (ми вважаємо, що площа отвору набагато менша за площу вільної поверхні). Застосуємо рівняння Бернуллі до точок  і
і 
 — атмосферний тиск, а висота
— атмосферний тиск, а висота  відлічується від рівня отвору. Звідси отримуємо
відлічується від рівня отвору. Звідси отримуємо (10.7)
(10.7)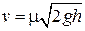 .
. =1100. Критичне значення числа Рейнольдса, тобто число
=1100. Критичне значення числа Рейнольдса, тобто число 


