
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В-87 Дослідження поведінки мікрочастинокСодержание книги
Поиск на нашем сайте
В потенціальній ямі Мета: ознайомитись із особливостями енергетичного спектру мікрочастинок, що перебувають в потенціальній ямі та навчитись визначати за допомогою отриманих експериментальних даних фізичні сталі та характеристики елементарних частинок. Устаткування: комп’ютерна програма “Частинка в потенціальній ямі”. Теоретичні відомості У квантовій фізиці частка, що рухається у вільному просторі, може мати будь-яку енергію. Її енергетичний спектр – суцільний. У частки, що рухається в силовому полі, що утримує її в обмеженій області простору, спектр власних значень енергії виявляється дискретним. Прикладом може служити фінітний (тобто обмежений) рух електрона в кулонівськім полі ядра атома Гідрогену. Дискретність енергетичних рівнів часток, замкнених в обмеженій області простору, випливає з двоїстої природи часток і є принциповою відмінністю квантової фізики від класичної. Простою фізичною моделлю фінітного руху може служити рух частки в одномірній «потенціальній ямі» з нескінченно високими стінками. Частка не може залишити область розміром L. Вона рухається в цій області, зазнаючи багаторазових відбивань від стінок. З хвильової точки зору між стінками в зустрічних напрямках рухаються дві хвилі де Бройля. Це нагадує картину двох зустрічних хвиль, що біжать по струні із закріпленими кінцями. Як і у випадку струни, стаціонарним станам відповідають стоячі хвилі, які утворяться за умови, що на довжині L укладається ціле число півхвиль: L = n · (λ / 2) (n = 1, 2, 3,...) (87.1) Таким чином, стаціонарним станам частки, замкненої в потенціальній ямі, відповідає дискретний набір довжин хвиль. Оскільки в квантово-механічному випадку довжина хвилі λ однозначно зв'язана з імпульсом частки: λ = h / p, а імпульс частки р визначає енергію її руху: E = p2 / (2m) (нерелятивістське наближення), то квантованою (дискретною) виявляється й енергія частки. Квантово-механічний розрахунок приводить до наступного виразу:
Тут m – маса частки, h – постійна Планка, E1 = h2 / (8m2) – енергія щонайнижчого стану. Варто звернути увагу, що квантово-механічна частка на відміну від класичної не може спочивати на дні потенціальної ями, тобто мати енергію E1 = 0. Це суперечило б співвідношенню невизначеностей Δx · Δpx ≥ h. (87.3) Дійсно, у частинки, що знаходиться у стані спокою, імпульс строго дорівнює нулю, отже, Δpx = 0. У той же час невизначеність координати частки Δx ~ L. Тому добуток Δx · Δpx у частки, що лежить на дні потенціальної ями, повинен був би дорівнювати нулю. Співвідношення невизначеностей дозволяє зробити оцінку мінімальної енергії E1 частки. Якщо прийняти, що в стані з мінімальною енергією px ≈ Δpx, то для мінімальної енергії E1 отримуємо вираз:
Ця груба оцінка дає правильне за порядком величини значення E1. Стоячі хвилі де Бройля, що утворяться під час руху частки в потенціальній ямі, це і є хвильові чи псі-функції, за допомогою яких квантова механіка описує стаціонарні стани мікрооб'єктів. Квадрат модуля |ψ|2 хвильової функції визначається як ймовірність перебування частки в різних точках простору. У комп'ютерній моделі можна змінювати ширину L потенціальної ями, а також масу m замкненої в ній частки. У лівому вікні висвічуються графічні зображення хвильових функцій ψ(x) чи квадратів їхніх модулів |ψ|2 для декількох стаціонарних станів (n = 1–5). У правому вікні зображується енергетичний спектр частки, тобто спектр можливих значень її енергії. Зверніть увагу, що енергетичні рівні опускаються із збільшенням ширини L потенціальної ями і маси m замкненої в ній частки. У комп'ютерній моделі маса частки виражається в масах протона mp = 1,67·10–27 кг. Отже, моделюються стани порівняно важких часток (ядер важких атомів), що опинились в потенціальній ямі із шириною порядку розмірів атомів.
Хід роботи Завдання 1. Ознайомлення із можливостями комп’ютерної моделі
1. Змінюючи ширину потенціальної ями х за незмінного значення маси частинки m, слідкувати за графічним зображенням хвильових функцій та квадратів їх модулів для різних стаціонарних станів. Прослідкувати за характером зміни енергетичного спектру частинки і зробити висновок про поведінку енергетичних рівнів при цьому. Рисунок 87.1 – Квантування енергії та ймовірність перебування мікрочастки в певному місці потенціальної ями
2. Змінюючи значення маси частинки m за незмінного значення ширини потенціальної ями х, слідкувати за графічним зображенням хвильових функцій та квадратів їх модулів для різних стаціонарних станів. Прослідкувати за зміною енергетичного спектру частинки і зробити висновок про поведінку енергетичних рівнів при цьому. Завдання 2. Визначення значення постійної Планка h 1. Згідно таблиці варіантів виставити у вікні інтерфейсу значення маси частинки. Таблиця 87.1 – Варіанти завдань
2. Змінюючи значення ширини потенціальної ями від мінімального до максимального значення, визначити із правого вікна (енергетичного спектру) значення енергії частинки для двох наведених в таблиці варіантів значень стаціонарних станів ni i nj. 3. Знайти для кожного значення х різницю енергій частинки для двох вказаних стаціонарних станів ΔEji. Оскільки згідно (87.2)
то побудувати графік залежності ΔEjі від 1/х2. 4. Визначити із графіка нахил k прямої залежності ΔEjі (1/х2)
Враховуючи, що згідно (87.5)
визначити значення постійної Планка h за допомогою формули
5. Визначити похибки знаходження значення h і порівняти отримане експериментальне значення із табличним. Завдання 3. Визначення маси частинки 1. Використовуючи визначене в пункті 4 значення k, а також значення постійної Планка h = 6.62·10-34 Дж·с, обчислити значення маси досліджуваної частинки. 2. Поділивши отримане значення маси частинки на значення масового коефіцієнту із таблиці варіантів (або із вікна інтерфейсу), знайти масу протона і порівняти із табличним значенням. Контрольні запитання 1. В чому полягає принципова відмінність у трактуванні властивостей мікрочастинок класичною і квантовою фізиками? 2. Що таке хвилі де Бройля? 3. Яка умова створення стоячих хвиль? 4. Який взаємозв’язок корпускулярних і хвильових характеристик мікрочастинок? 5. Сформулюйте співвідношення невизначеностей Гейзенберга. 6. З чим пов’язана невизначеність енергії згідно співвідношень невизначеностей Гейзенберга? 7. Що таке стаціонарний стан атома? 8. Яку інформацію несе квадрат модуля хвильової функції? Література 1. Курик М.В., Цмось В.М. Фізика твердого тіла. Нав.посібник – К.: Вища школа, 1985, - 246 с. (Розділ 10). 2. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – 791 с. (Глави 2,3). 3. Лучицький Р.М., Галущак М.О. Фізика твердого тіла.Навч. пос.– Івано-Франківськ: Факел, 2008, – 250с. Додаткова література 4. Болеста І.М. Фізика твердого тіла. Навч. пос. – Львів: Видавн. центр ЛНУ імені Івана Франка.2003. – 480с. 5. Бушманов Б.Н., Хромов Ю.А. Фізика твердого тела: Уч. Пособие для вузов. – М.: Высшая школа, 1971. – 224 с. 6. Блейкмор Дж. Физика твердого тела / Пер. с англ. Под ред. Д.Т. Андрианова. – М.: Мир, 1988. – 608 с. 7. Епифанов Г.И. Физика твердого тела: Уч. Пособие. – Высшая школа, 1977. – 288 с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.38 (0.005 с.) |

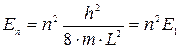 . (87.2)
. (87.2) . (87.4)
. (87.4)
 , (87.5)
, (87.5)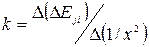 . (87.6)
. (87.6) ,
, . (87.7)
. (87.7)


