
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція розподілу ймовірності.Содержание книги
Поиск на нашем сайте
Нехай існує сукупність дуже великої кількості N однакових молекул (наприклад, газ), що знаходиться в рівноважному стані. Припустимо, що деяка величина х, що характеризує молекулу (наприклад, обертальна чи коливальна енергія молекули), може приймати ряд дискретних значень:
Якби удалося виміряти одночасне значення величини Величина
називається імовірністю того, що величина Зрозуміло, що
Таким чином, сума імовірностей усіх можливих значень величини х дорівнює одиниці. Припустимо, що молекули характеризуються значеннями двох величин (наприклад, коливальної й обертальної енергій), кожна з який може приймати дискретні значення xi i yk. Відповідно до визначення (1.1) імовірності цих значень рівні
Якщо значення однієї з величин не залежить від того, яке значення має інша, то величини x i y називаються статистично незалежними. Знайдемо ймовірність
Ми прийшли до теореми про добуток ймовірностей, відповідно до якої імовірність одночасної появи статистично незалежних подій дорівнює добутку імовірностей цих подій. (У розглянутому вище випадку подією є те, що величина має дане значення.) Якщо ймовірність значення xi величини
Поділимо цю суму на
Отримана нами формула дозволяє, якщо ми знаємо ймовірності різних значень величини х, знайти середнє значення цієї величини. Тепер розглянемо випадок, коли величина х, що характеризує молекулу, може приймати неперервний ряд значень від У розглянутому випадку правомірним є питання про те, яка імовірність
(індекс Помноживши
Інтеграл від
Наслідком цього є співвідношення
Формула (20.8) є аналогом формули (20.2). З умови (20.8) ми бачимо, що площа, обмежена графіком функції Вираз
дає суму значень
Ця формула є аналогом формули (20.5). Якщо підставити в формулу (20.9) замість
Згідно цієї формулі можна підрахувати, наприклад, середнє значення
Розподіл Максвелла. Теплова швидкість молекул газу – це деяка усереднена характеристика теплового руху частинок. У дійсності різні молекули рухаються з різними швидкостями і можна поставити питання про розподіл молекул за швидкостями: скільки (у середньому) з наявних у газі молекул має ті чи інші швидкості? Стан газу будемо вважати рівноважним. Для наочного уявлення швидкостей молекул газу скористаємося наступним прийомом. Введемо уявний простір швидкостей (
Якщо збільшити кількість молекул газу в деяку кількість разів, то в стільки ж разів зросте усюди густина м -точок. Отже, густина м-точок пропорційна
Знаючи вид функції
На рисунку 20.1 зображена штриховою лінією кульовий шар радіуса
Поділивши цей вираз на кількість молекул
Згідно формули (20.6) вираз Функцію
де
яка називається умовою нормування функції Відповідний розрахунок дає для коефіцієнта пропорційності
Ця функція називається функцією розподілу Максвелла. Відзначимо, що під знаком експоненти у формулі (20.19) знаходиться відношення кінетичної енергії молекули (що відповідає даному значенню швидкості
Провівши диференціювання, прийдемо до рівняння
Перший множник (експонент) перетворюється в нуль при Звідки
Відповідно до формул (20.10) і (20.12) середнє (за молекулами) значення модуля швидкості
Таким чином, середня швидкість молекул (її також називають середньою арифметичною швидкістю) має значення
Корінь квадратний з виразу (20.21) дає середню квадратичну швидкість молекул:
Помноживши чисельник і знаменник підкореневих виразів в (20.20), (20.22) і (20.23) на сталу Авогадро і пам’ятаючи, що
Знайдемо середню швидкість молекул азоту (
Для кисню отримується при тій самій температурі Якщо існує суміш газів, яка знаходиться у рівновазі, то в межах кожного сорту молекул має місце розподіл Максвелла зі своїм значенням Відповідно до формули (20.7) кількість молекул, швидкості яких укладені в межах від
(
тобто покласти
де
Цей вираз являє собою функцію розподілу Максвелла, записану в змінній Проінтегрувавши вираз (20.27) в межах від
В таблиці 1 наведені відносні кількості молекул Згідно формулам (20.24)
(див. рисунок 20.2). Таким чином, середня і середня квадратична швидкості більше від найбільш ймовірної швидкості на 13 і 22% відповідно. З (20.26) і (20.30) витікає, що Таблиця 20.1 – Відносна доля молекул, що мають різну відносну швидкість
Таблиця 20.2 – Значення температури
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.134.161 (0.007 с.) |

 ,
,  , …,
, …,  , …
, … у всіх
у всіх  молекул, то виявилося б, що у
молекул, то виявилося б, що у  молекул величина
молекул величина  молекул –
молекул –  молекул – значення
молекул – значення  (20.1)
(20.1) . Тому
. Тому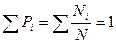 . (20.2)
. (20.2) ,
,  . (20.3)
. (20.3) того, що статистично незалежні величини мають одночасно значення
того, що статистично незалежні величини мають одночасно значення  . З (20.3) випливає, що значення xi мають
. З (20.3) випливає, що значення xi мають  молекул. Внаслідок статистичної незалежності у цих
молекул. Внаслідок статистичної незалежності у цих  молекул значення
молекул значення  молекул. Поділимо це число на
молекул. Поділимо це число на  . (20.4)
. (20.4) , то відповідно до формули (20.1) у
, то відповідно до формули (20.1) у  молекул
молекул  молекул буде рівна
молекул буде рівна 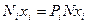 , а сума значень
, а сума значень  .
. . (20.5)
. (20.5) до
до  (наприклад,
(наприклад,  i
i  можуть бути рівними
можуть бути рівними 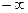 і
і  ). Прикладами таких величин можуть служити модуль поступальної швидкості чи кінетична енергія молекули. У цьому випадку число можливих значень х нескінченно велико, а кількість молекул хоча і дуже велика, але скінчена. Тому питання про те, яка кількість молекул має точно задане значення величини х, не має змісту - ця кількість дорівнює нулю.
). Прикладами таких величин можуть служити модуль поступальної швидкості чи кінетична енергія молекули. У цьому випадку число можливих значень х нескінченно велико, а кількість молекул хоча і дуже велика, але скінчена. Тому питання про те, яка кількість молекул має точно задане значення величини х, не має змісту - ця кількість дорівнює нулю. того, що величина має значення, укладені в межах малого інтервалу
того, що величина має значення, укладені в межах малого інтервалу  , розташованого в околиці значення, рівного
, розташованого в околиці значення, рівного  (20.6)
(20.6) указує значення
указує значення  називається функцією розподілу імовірності або густиною ймовірності.
називається функцією розподілу імовірності або густиною ймовірності. на повну кількість молекул
на повну кількість молекул  , які мають значення
, які мають значення  . (20.7)
. (20.7) .
. . (20.8)
. (20.8) дає суму значень
дає суму значень 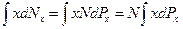 (20.9)
(20.9) . (20.10)
. (20.10) , прийдемо до формули
, прийдемо до формули . (20.11)
. (20.11) :
: . (20.12)
. (20.12) - простір), у якому будемо відкладати уздовж прямокутних координатних вісей значення компонент швидкостей
- простір), у якому будемо відкладати уздовж прямокутних координатних вісей значення компонент швидкостей  ,
,  ,
,  окремих молекул (рис. 1). Тоді кожній молекулі буде відповідати в просторі швидкостей точка. Щоб відрізнити цю точку від довільної точки
окремих молекул (рис. 1). Тоді кожній молекулі буде відповідати в просторі швидкостей точка. Щоб відрізнити цю точку від довільної точки  Оскільки газ знаходиться в рівновазі, усі напрямки руху молекул рівноправні, унаслідок чого розташування м -точок відносно початку координат виявляється сферично-симетричним. Тому густина м -точок (їхня кількість в одиниці об'єму
Оскільки газ знаходиться в рівновазі, усі напрямки руху молекул рівноправні, унаслідок чого розташування м -точок відносно початку координат виявляється сферично-симетричним. Тому густина м -точок (їхня кількість в одиниці об'єму 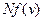 (20.3)
(20.3) , можна вирішити ряд задач. Наприклад, знайти кількість молекул
, можна вирішити ряд задач. Наприклад, знайти кількість молекул  , компоненти швидкості яких укладені в межах інтервалів
, компоненти швидкості яких укладені в межах інтервалів  ,
,  ,
,  , що лежать в околиці геометричної точки з координатами
, що лежать в околиці геометричної точки з координатами  . (20.14)
. (20.14) . Молекули, м -точки яких знаходяться в цьому кульовому шарі, мають швидкості, модулі яких лежать в інтервалі від
. Молекули, м -точки яких знаходяться в цьому кульовому шарі, мають швидкості, модулі яких лежать в інтервалі від  . Щоб знайти число
. Щоб знайти число  таких молекул, потрібно помножити густину м -точок, що відповідає даному значенню
таких молекул, потрібно помножити густину м -точок, що відповідає даному значенню  :
: . (20.15)
. (20.15) того, що модуль швидкості молекули в межах від
того, що модуль швидкості молекули в межах від  . (20.16)
. (20.16) є функцією розподілу ймовірності значень
є функцією розподілу ймовірності значень  отримав теоретично Д.К.Максвелл. Вона має вигляд
отримав теоретично Д.К.Максвелл. Вона має вигляд , (20.17)
, (20.17) – маса молекули,
– маса молекули, 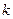 – стала Больцмана,
– стала Больцмана,  – абсолютна температура. Коефіцієнт пропорційності
– абсолютна температура. Коефіцієнт пропорційності  визначається з умови
визначається з умови , (20.18)
, (20.18) . Напишемо з урахуванням цього остаточний вираз для функції розподілу молекул газу за швидкостями:
. Напишемо з урахуванням цього остаточний вираз для функції розподілу молекул газу за швидкостями: . (20.19)
. (20.19) , що характеризує середнє (за молекулами) значення цієї енергії.
, що характеризує середнє (за молекулами) значення цієї енергії. Графік функції (20.19) наведений на рис. 2. Найбільш ймовірною буде, мабуть, швидкість, що відповідає максимуму функції
Графік функції (20.19) наведений на рис. 2. Найбільш ймовірною буде, мабуть, швидкість, що відповідає максимуму функції  можна знайти, якщо прирівняти до нуля похідну
можна знайти, якщо прирівняти до нуля похідну  . Опустивши у виразі (20.19) множники, що не залежать від
. Опустивши у виразі (20.19) множники, що не залежать від  .
. .
. , а третій множник (
, а третій множник (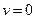 . Однак з графіка бачимо, що значення
. Однак з графіка бачимо, що значення  .
. . (20.20)
. (20.20) ,
, . (20.21)
. (20.21) . (20.22)
. (20.22) . (20.23)
. (20.23) рівно газовій сталій
рівно газовій сталій  , а
, а  – молярній масі газу
– молярній масі газу  , прийдемо до результатів
, прийдемо до результатів ,
,  ,
, 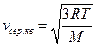 . (20.24)
. (20.24) ) при кімнатній температурі (293К):
) при кімнатній температурі (293К): .
. , а для водню
, а для водню  . Таким чином, молекули повітря за секунду проходять шлях, що дорівнює майже
. Таким чином, молекули повітря за секунду проходять шлях, що дорівнює майже 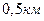 .
. (20.25)
(20.25) , (20.26)
, (20.26) . Тоді замість
. Тоді замість  треба підкласти у (20.25)
треба підкласти у (20.25)  , а замість
, а замість  . В результаті отримаємо формулу
. В результаті отримаємо формулу , (20.27)
, (20.27) – кількість молекул, відносні швидкості яких укладені в межах від
– кількість молекул, відносні швидкості яких укладені в межах від  до
до  . Функція
. Функція  є функція розподілу ймовірності значень
є функція розподілу ймовірності значень  . (20.28)
. (20.28) до
до  , отримаємо кількість молекул
, отримаємо кількість молекул  , відносні швидкості котрих знаходяться в цих межах:
, відносні швидкості котрих знаходяться в цих межах: . (20.29)
. (20.29) , розраховані згідно формули (20.29) для різних інтервалів швидкостей. З таблиці випливає, що у 70,7% молекул швидкість відрізняється від найбільш ймовірної не більше ніж на 50%. Швидкостями, що перевищують найбільш ймовірну більш ніж у три рази, володіють лише 0,04% молекул, а швидкості, що перевищують найбільш ймовірну більш ніж у п'ять разів, спостерігається в однієї з 12 мільярдів молекул. Ці дані підтверджують висловлене раніше твердження про те, що швидкості молекул в основному групуються поблизу найбільш ймовірного (з тим же правом можна сказати - поблизу середнього) значення.
, розраховані згідно формули (20.29) для різних інтервалів швидкостей. З таблиці випливає, що у 70,7% молекул швидкість відрізняється від найбільш ймовірної не більше ніж на 50%. Швидкостями, що перевищують найбільш ймовірну більш ніж у три рази, володіють лише 0,04% молекул, а швидкості, що перевищують найбільш ймовірну більш ніж у п'ять разів, спостерігається в однієї з 12 мільярдів молекул. Ці дані підтверджують висловлене раніше твердження про те, що швидкості молекул в основному групуються поблизу найбільш ймовірного (з тим же правом можна сказати - поблизу середнього) значення.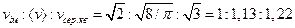 (20.30)
(20.30)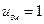 ,
, 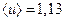 ,
,  .
.
 , %
, %
 На рисунку 20.3 приведені графіки розподілу Максвелла для двох значень температури. Графіки можна трактувати або як відповідні різним значенням температури, або як відповідні різним значенням маси молекул. Площа, обмежена графіком, в обох випадках рівна одиниці.
На рисунку 20.3 приведені графіки розподілу Максвелла для двох значень температури. Графіки можна трактувати або як відповідні різним значенням температури, або як відповідні різним значенням маси молекул. Площа, обмежена графіком, в обох випадках рівна одиниці.


