
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання 1. Ознайомлення з роботою комп’ютерної програми та явищем інтерференції НьютонаСодержание книги
Поиск на нашем сайте
1. Розглянути інтерференційну картину, отриману з допомогою: монохроматичного світла; біхроматичного світла з різною комбінацією двох монохроматичних світлових хвиль, а також з різним міжчастотним інтервалом; прямокутного спектра з різною його шириною для плоскої поверхні скляної пластини. 2. Виконати пункт 1 для сферичної поверхні пластини.
Таблиця 65.1 – Варіанти завдань
Завдання 2. Розрахунок ширини смуги пропускання світлофільтра 1. Встановити прапорець у вікні „Прямокутний спектр“. Вирізати з неперервного спектру вузьку (λ<50) смугу певного кольору (задається викладачем). 2. Змінюючи радіус кривизни лінзи (для випадку плоскої поверхні пластини), добитися на краю інтерференційної картини перекриття спектрів (розмивання інтерференційної картини). 3. Підрахувати максимальну кількість чітких світлих кілець. За формулою (65.10) визначити ширину смуги пропускання світлофільтра. 4. Змінити ширину смуги так, щоб 5. Виконавши пункт 4 4-5 разів, побудувати графіки залежностей 6. Із графіка 7. Порівняти експериментально отримане значення
Завдання 3. Визначення довжини хвилі монохроматичного світла 1. Отримати зображення інтерференційної картини (довжина хвилі задається викладачем) використовуючи плоску поверхню скляної пластини. 2. Виміряти радіус 5-7 кілець, як сказано в завданні 2. 3. Побудувати залежність 4. Визначити з графіка нахил прямої і за допомогою отриманого значення
Обчислити відносні і абсолютні похибки для величин R і λ. Результати вимірювання записати в стандартній формі. Зробити відповідні висновки до кожного завдання.
Контрольні запитання 1. В чому полягає явище інтерференції світла? 2. Які промені називають когерентними? 3. Які є способи отримання когерентних джерел? 4. Як отримати кільця Ньютона? 5. Чим відрізняються кільця Ньютона у відбитому і прохідному світлі? 6. Як використовуються кільця Ньютона для оцінки чистоти поверхні? 7. Як зміниться вигляд кілець, якщо простір між лінзою та пластинкою заповнити водою?
Література 1. Лопатинський І.Є. Курс фізики. Фізика для інженерів. – Л.: „Бескид Біт”, 2002. 2. Кучерук І.М., Дущенко В.П. Загальна фізика. Т.3. – К.: „Вища школа”, 1987 – 1991. 3. Бушок Г.Ф. і ін. Курс фізики. Кн. 2. – К.: „Либідь”, 2001. 4. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики. Т.3. – К.: „Техніка”, 2001. 5. Трофимова Т.И. Курс физики. – М.: “Высшая школа”, 1990.
В-68 Вивчення дифракції Френеля від круглого отвору Мета: ознайомитися з дифракцією Френеля від круглого отвору, визначити довжину світлової хвилі та радіуси зон Френеля. Прилади і матеріали: програма комп’ютерної лабораторної роботи “Дифракція Френеля від круглого отвору”, лінійка. Теоретичні відомості Дифракція світла – оптичне явище, пов’язане із зміною напряму поширення світлових хвиль (порівняно з напрямом, передбаченим геометричною оптикою) та з просторовим перерозподілом їх інтенсивності під впливом перешкод і неоднорідностей середовища на їхньому шляху. Під дифракцією розуміють будь-яке відхилення від прямолінійного поширення світла, якщо воно не зумовлене відбиванням, заломленням або викривленням променів у середовищах, в яких показник заломлення безперервно змінюється. Дифракція світла зумовлена його хвильовою природою. Дифракція світла пояснюється принципом Гюйгенса-Френеля: нескінчено малі елементи хвильової поверхні є джерелами вторинних сферичних когерентних хвиль, амплітуда яких пропорційна до площі елемента; амплітуда коливань в довільній точці простору за хвильовою поверхнею визначається суперпозицією таких вторинних хвиль. Явища дифракції прийнято розрізняти залежно від відстані до перешкоди, встановленої на шляху поширення світла, до джерела і екрана, на якому спостерігається дифракційна картина. Якщо ці відстані, чи одна з них, не дуже великі, то дифракційні явища називають дифракцією Френеля (дифракція сферичних хвиль) або дифракцією в непаралельних променях. Дифракція Фраунгофера (дифракція в паралельних променях) – дифракція світла, що спостерігається на таких відстанях, для яких кутові розміри оптичних неоднорідностей набагато менші ніж відношення довжини світлової хвилі до лінійних розмірів цих неоднорідностей. Між дифракціями Френеля і Фраунгофера не існує принципової різниці і різкої межі. Робоча формула Розглянемо проходження світла через круглий отвір DD (рис. 68.1). Проведемо з точки О конічні поверхні M1OM1′, M2OM2′, M3OM3′ і т. д. до перетину з поверхнею сферичної хвилі DM0D. Довжини їх виберемо так, що відстань від точок M0, M1, M2, … до точки О збільшується на довжину півхвилі
Оскільки Підставивши цей вираз у формулу (68.1), одержимо
Визначимо кількість зон Френеля j, що вміщуються в отворі екрана. З рисунку 68.1 маємо
Оскільки Враховуючи, що
Радіус останньої зони Френеля збігається з радіусом отвору, тобто
Для малих кутів дифракції φ (рисунок 68.2) сумарна амплітуда виражається через спеціальну функцію Бесселя
Ця формула відіграє першорядну роль у дифракційній теорії оптичних приладів. Кутові радіуси темних кілець наближено визначаються формулою
Лінійні розміри радіуса першого темного кільця приблизно дорівнюють
де L – відстань від отвору до екрана.
Інтерфейс програми
Зверніть увагу: лінійні розміри дифракційної картини, отриманої на екрані, є в k -разів більшими за справжні розміри.
Завдання 1. Ознайомлення з роботою комп’ютерної програми та явищем дифракції від круглого отвору Розглянути дифракційну картину отриману з допомогою: 1. Монохроматичного світла; 2. Біхроматичного світла з різною комбінацією двох монохроматичних світлових хвиль, а також з різним міжчастотним інтервалом; 3. Прямокутного спектра з різною його шириною для плоскої поверхні скляної пластини.
Таблиця 68.1 – Варіанти завдань
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.224 (0.007 с.) |

 залишилося незмінним. Повторити пункти 1, 2, 3.
залишилося незмінним. Повторити пункти 1, 2, 3. і
і  .
. , середню довжину хвилі, що пропускає „світлофільтр“.
, середню довжину хвилі, що пропускає „світлофільтр“. і
і  .
. .
. обчислити довжину хвилі, використавши радіус кривизни, знайдений у завданні 2.
обчислити довжину хвилі, використавши радіус кривизни, знайдений у завданні 2. світла, що падає на отвір (
світла, що падає на отвір ( ,
,  , …,
, …,  ). Утворені конуси поділять поверхню DM0D на сукупність рівновеликих кільцевих зон (зон Френеля).
). Утворені конуси поділять поверхню DM0D на сукупність рівновеликих кільцевих зон (зон Френеля). Визначимо висоту сегмента hj. З трикутників SMjC і CMjO маємо
Визначимо висоту сегмента hj. З трикутників SMjC і CMjO маємо ,
, звідки
звідки . (68.1)
. (68.1)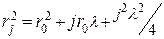 . Якщо
. Якщо 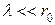 і
і  , то членом
, то членом  можна знехтувати і тоді
можна знехтувати і тоді  .
. . (68.2)
. (68.2) .
. , то величиною
, то величиною  можна знехтувати.
можна знехтувати. . (68.3)
. (68.3) . Тоді кількість зон Френеля n обчислимо за формулою
. Тоді кількість зон Френеля n обчислимо за формулою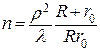 . (68.4)
. (68.4) Світлові хвилі від першої і другої зон, дійшовши до точки О, будуть взаємно послаблятися, так що в точці О дія першої зони практично знищується дією другої зони, дія другої зони протилежна до дії третьої зони і т. д. Якщо отвір DD такий, що в ньому вміщується тільки дві зони, то в точці О практично не буде світла (дві сусідні зони взаємно послаблюють одна одну). Отже, ми побачимо на екрані в центрі темний круг, оточений світлим кільцем. Для отвору в якому вкладається три зони Френеля на екрані в центрі буде світлий круг, оточений темним кільцем, за яким знову буде світле кільце. В загальному, за парної кількості зон, в центрі буде темне кільце, оточене почергово світлими і темними кільцями; за непарної кількості зон – у центрі буде світлий круг, почергово оточений темними і світлими кільцями. Чим більший отвір, тим розміри кілець будуть меншими.
Світлові хвилі від першої і другої зон, дійшовши до точки О, будуть взаємно послаблятися, так що в точці О дія першої зони практично знищується дією другої зони, дія другої зони протилежна до дії третьої зони і т. д. Якщо отвір DD такий, що в ньому вміщується тільки дві зони, то в точці О практично не буде світла (дві сусідні зони взаємно послаблюють одна одну). Отже, ми побачимо на екрані в центрі темний круг, оточений світлим кільцем. Для отвору в якому вкладається три зони Френеля на екрані в центрі буде світлий круг, оточений темним кільцем, за яким знову буде світле кільце. В загальному, за парної кількості зон, в центрі буде темне кільце, оточене почергово світлими і темними кільцями; за непарної кількості зон – у центрі буде світлий круг, почергово оточений темними і світлими кільцями. Чим більший отвір, тим розміри кілець будуть меншими. Так як розміри зон Френеля залежать від довжини світлової хвилі, то і вигляд дифракційної картини буде залежати від довжини хвилі.
Так як розміри зон Френеля залежать від довжини світлової хвилі, то і вигляд дифракційної картини буде залежати від довжини хвилі. , де
, де  , r –радіус отвору, φ – кут дифракції. Корінь, що відповідає першому мінімуму інтенсивності, тобто визначає кутові розміри центральної світлої плями, визначається з умови
, r –радіус отвору, φ – кут дифракції. Корінь, що відповідає першому мінімуму інтенсивності, тобто визначає кутові розміри центральної світлої плями, визначається з умови . (68.5)
. (68.5) , де m =1, 2, 3,... (68.6)
, де m =1, 2, 3,... (68.6) . (68.7)
. (68.7)



