
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В-64 Вивчення явища інтерференції на прикладіСодержание книги
Поиск на нашем сайте
Досліду Юнга Мета: ознайомитися з явищем інтерференції у досліді Юнга. Прилади і матеріали: Програма комп’ютерної лабораторної роботи “Дослід Юнга”, масштабна лінійка. Теоретичні відомості Хвильові властивості світла досить яскраво проявляються в явищах інтерференції, дифракції та поляризації світла. Інтерференцією світла називається явище, яке виникає при додаванні світлових хвиль і полягає в тому, що інтенсивність результуючої світлової хвилі, залежно від різниці фаз хвиль, що додаються, може бути більшою або меншою за суму їхніх інтенсивностей. Інтерференція світла у будь-якій точці простору спостерігається тільки для когерентних світлових хвиль, тобто таких, що мають сталу різницю фаз між однаково напрямленими світловими коливаннями однакової частоти, що приходять у цю точку. Незалежні когерентні джерела світла реалізувати практично неможливо. В оптиці відомі методи утворення когерентних пучків від звичайних джерел світла. Перший з них полягає ось у чому. Когерентні хвилі випромінюються одним точковим випромінювачем в різних напрямках, після необхідних відбивань і заломлень їм надаються такі напрями поширення, при яких вони можуть перетинатися і інтерферувати (йдеться про інтерференцію Френеля; ця група методів дістала назву методів поділу хвильового фронту; вона реалізується за допомогою бідзеркала і біпризми Френеля, дзеркала Ллойда, щілини Юнга і т.п.). Другий метод отримання когерентних пучків полягає в розщепленні однієї хвилі на кілька при відбиванні і заломленні на поверхнях (цей метод називають метод поділу амплітуд, йдеться про інтерференцію Ньютона; вона реалізується в різних типах інтерферометрів; прикладом інтерференційних картин, утворювальних в результаті поділу амплітуди, є смуги однакової товщини і однакового нахилу, кільця Ньютона). Інтерференційна картина являє собою послідовність світлих і темних смуг – максимумів і мінімумів. Умови екстремумів мають такий вигляд:
де Δ – різниця ходу інтерферуючих пучків; m = 0, 1, 2, … – порядок інтерференційного максимуму і мінімуму,
Інтерфейс програми “Дослід Юнга”
Першим дослідом, яким доведено можливість отримати інтерференцію світлових хвиль, був дослід Юнга. Користуючись схемою цього досліду, можна визначити довжину світлової хвилі. Розглянемо хід променів в дослідній установці (рисунок 64.1).
Рисунок 64.1
Світло від джерела S через вузьку діафрагму С спрямовується на подвійну щілину Н. Лінза L фокусує світлові промені. Світлові промені від щілини пропускають через світлофільтри F. У мікроскоп М спостерігають інтерференційну картину.
З рисунка 64.2 маємо:
де
Тоді шукані відстані згідно (64.3) дорівнюють:
Відстань між обраними темними смугами
звідки довжина хвилі
де (n – кількість світлих смуг між досліджуваними темними смугами).
Порядок виконання Завдання 1 Ознайомлення з комп’ютерною програмою 1. Ознайомитися з інтерфейсом комп’ютерної програми “Дослід Юнга”. 2. Міняючи відстань між щілинами, відстань до екрану, і довжину хвилі визначити, як міняється інтерференційна картина при зміні цих параметрів. 3. Міняючи параметри “Монохроматичний”, “Біхроматичний” та “Прямокутний спектр” (див. Інтерфейс програми) отримати чітку інтерференційну картину для різних довжин хвиль.
Завдання 2 Визначення довжини світлової хвилі 1. Для певної довжини хвилі (задається викладачем) при “Монохроматичному” досліді добитися того, щоб на екрані укладалася ціла кількість темних смуг n. 2. Роздрукувавши з програми інтерференційну картину, визначити розмір зображення інтерференційної картини ( 3. Дослід повторити 4 рази для інших параметрів L i d. 4. Визначити середнє значення і похибки для довжини світлової хвилі та записати їх у висновок.
Завдання 3 Визначення розміру інтерференційної картини 1. При фіксованому значенні L і λ (задається викладачем) провести “Монохроматичний” дослід так, щоб на екрані укладалася ціла кількість темних смуг n. 2. Дослід повторити 10 раз, міняючи параметр d. 3. З отриманих результатів побудувати графік залежності N = f(d). 4. Обчислити розмір зображення інтерференційної картини 5. Результати записати у висновку.
Таблиця 64.1 – Варіанти завдань
Контрольні запитання 1. У чому полягає суть явища інтерференції? 2. Які хвилі називаються когерентними? 3. Охарактеризуйте методи утворення когерентних пучків. 4. Що таке оптична різниця ходу? 5. Як міняється інтерференційна картина, якщо дослід провести при параметрі “Прямокутний спектр”, а не “Монохроматичний”? 6. Чим визначається кількість видимих інтерференційних смуг? Література 1 Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики. Т.: 3. – К.: “Техніка”, 2001. 2 Бушок Г.Ф. і ін. Курс фізики. Кн. 2. – К.: „Либідь”, 2001. 3 Лопатинський І.Є. Курс фізики. Фізика для інженерів. – 4 Трофимова Т.И. Курс физики. – М.: “Высшая школа”, 1990. B-65 Дослідження інтерференції світла Мета: ознайомитися з явищем інтерференції на прикладі кілець Ньютона, визначити пропускну здатність світлофільтра, радіус кривизни лінзи та довжину світлової хвилі. Прилади і матеріали: програма комп’ютерної лабораторної роботи “Кільця Ньютона”, лінійка. Теоретичні відомості Інтерференцією світла називають явище, яке виникає внаслідок додавання світлових хвиль і полягає в тому, що інтенсивність результуючої світлової хвилі (залежно від різниці фаз хвиль, які додаються) може бути більшою або меншою за суму їхніх інтенсивностей. Інтерференція світла спостерігається тільки коли додаються когерентні хвилі, тобто такі, що мають сталу різницю фаз світлових коливань протягом певного проміжку часу та однакову частоту коливань. В природі не існує світлових джерел, які би випромінювали когерентні хвилі. Проте в оптиці відомі методи утворення когерентних пучків від звичайних джерел світла. Розглянемо один з цих методів – метод розділення амплітуд, який використовується, зокрема, для отримання інтерференційної картини Ньютона і полягає в розщепленні однієї хвилі на кілька, внаслідок відбивання і заломлення на поверхнях. Загальні умови інтерференційних екстремумів мають такий вигляд:
де Δ – різниця ходу інтерферуючих хвиль; k = 0, 1, 2,...– порядок інтерференційного максимуму і мінімуму; λ–довжина світлової хвилі. Кільця Ньютона – приклад інтерференційної картини у тонких прозорих плівках різної товщини, – як інтерференційні смуги однакової товщини. Якщо на прозору плівку падає паралельний пучок світла, то на верхній і нижній її поверхнях він роздвоюється (частково відбивається, частково заломлюється). Таким чином, у відбитому і прохідному світлі виникає інтерференційна картина між когерентними променями. Різниця ходу в загальному випадку визначається товщиною плівки, кутом падіння променів та показником заломлення плівки і середовища. Умови відбивання світла на верхній і нижній поверхні плівки різні. На нижній поверхні (скло-повітря) відбивання відбувається з втратою півхвилі, на верхній – без втрати. Вираз для оптичної різниці ходу має вигляд:
Робоча формула
  відображає зміну фази хвилі, відбитої від оптично більш густого середовища (точка С). У відповідності з (65.4) різниця ходу хвиль в даному експерименті визначається тільки товщиною повітряного шару, тому вона є однаковою для всіх хвиль, відбитих на однаковій відстані від геометричного центра системи (точка О). Внаслідок цього інтерференційна картина має вигляд концентричних кілець. В центрі картини, де відображає зміну фази хвилі, відбитої від оптично більш густого середовища (точка С). У відповідності з (65.4) різниця ходу хвиль в даному експерименті визначається тільки товщиною повітряного шару, тому вона є однаковою для всіх хвиль, відбитих на однаковій відстані від геометричного центра системи (точка О). Внаслідок цього інтерференційна картина має вигляд концентричних кілець. В центрі картини, де  , спостерігають темний круг, що відповідає різниці ходу відбитих хвиль , спостерігають темний круг, що відповідає різниці ходу відбитих хвиль  . Результат інтерференції залежить від оптичної різниці ходу хвиль. Зв’язок між радіусом інтерференційного кільця r, радіусом кривизни лінзи R і довжиною хвилі . Результат інтерференції залежить від оптичної різниці ходу хвиль. Зв’язок між радіусом інтерференційного кільця r, радіусом кривизни лінзи R і довжиною хвилі  можна знайти з використанням цілком простих геометричних міркувань. З ΔBEF (рис.) маємо: можна знайти з використанням цілком простих геометричних міркувань. З ΔBEF (рис.) маємо:  . Оскільки лінза має великий радіус кривизни, то можна записати – . Оскільки лінза має великий радіус кривизни, то можна записати –  , звідки , звідки  , а тому , а тому  . Радіуси світлих кілець знайдемо з умови максимуму – . Радіуси світлих кілець знайдемо з умови максимуму –  : :
а радіуси темних кілець
Звідси
У виразах (65.4) і (65.6) Оскільки практично не вдається досягти щільного прилягання пластини до лінзи, то більш точний результат буде, коли визначається R за різницею радіусів двох довільних кілець
Підрахунок темних кілець починається від k=0, тобто від самого центра інтерференційної картини. Підрахунок світлих кілець починається з одиниці (k=1). Для великих порядків інтерференції може відбуватися перекриття спектрів, що приводить до розмивання інтерференційної картини. Очевидно, що умовою зникнення інтерференційної картини є
звідки
Інтерфейс програми “Кільця Ньютона”
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.4 (0.007 с.) |

 (умова максимуму); (64.1)
(умова максимуму); (64.1) (умова мінімуму), (64.2)
(умова мінімуму), (64.2) – довжина світлової хвилі.
– довжина світлової хвилі.


 , (64.3)
, (64.3)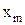 – відстань від максимуму та мінімуму порядку m до О1; L – відстань від подвійної щілини до екрану; d – відстань між центрами щілин (замість S1D беремо d, оскільки кут
– відстань від максимуму та мінімуму порядку m до О1; L – відстань від подвійної щілини до екрану; d – відстань між центрами щілин (замість S1D беремо d, оскільки кут  досить малий). Знайдемо для двох довільних темних смуг на екрані їх відстань від точки О1. Для цього запишемо умови мінімуму інтерференції:
досить малий). Знайдемо для двох довільних темних смуг на екрані їх відстань від точки О1. Для цього запишемо умови мінімуму інтерференції: . (64.4)
. (64.4) . (64.5)
. (64.5) ,
,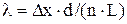 , (64.6)
, (64.6) ) за допомогою лінійки. На основі формули (64.6) визначити довжину світлової хвилі в досліді Юнга.
) за допомогою лінійки. На основі формули (64.6) визначити довжину світлової хвилі в досліді Юнга. , де
, де  – тангенс кута нахилу прямої на графіку залежності N = f(d). Порівняйте його із
– тангенс кута нахилу прямої на графіку залежності N = f(d). Порівняйте його із  (умова максимуму); (65.1)
(умова максимуму); (65.1) (умова мінімуму), (65.2)
(умова мінімуму), (65.2) . (65.3)
. (65.3) Кільця Ньютона спостерігаються тоді, коли сферична поверхня опуклої лінзи великого радіуса кривизни стикається з плоскою поверхнею. Внаслідок цього між лінзою і пластинкою утворюється повітряний шар змінної товщини (рис.). Проведемо розрахунки кілець Ньютона, що спостерігаються у відбитому світлі. У цьому випадку інтерферуватимуть промені, відбиті від верхньої і нижньої меж повітряного шару (точки С і В відповідно). Отже, лінії максимумів та мінімумів проходять через точки, що відповідають однаковій товщині повітряного шару і тому називаються смугами однакової товщини. Якщо промені падають нормально на плоску поверхню лінзи, то внаслідок малої кривизни лінзи можна вважати, що відбиваються вони теж вздовж нормалі. Для різниці ходу променів дістанемо
Кільця Ньютона спостерігаються тоді, коли сферична поверхня опуклої лінзи великого радіуса кривизни стикається з плоскою поверхнею. Внаслідок цього між лінзою і пластинкою утворюється повітряний шар змінної товщини (рис.). Проведемо розрахунки кілець Ньютона, що спостерігаються у відбитому світлі. У цьому випадку інтерферуватимуть промені, відбиті від верхньої і нижньої меж повітряного шару (точки С і В відповідно). Отже, лінії максимумів та мінімумів проходять через точки, що відповідають однаковій товщині повітряного шару і тому називаються смугами однакової товщини. Якщо промені падають нормально на плоску поверхню лінзи, то внаслідок малої кривизни лінзи можна вважати, що відбиваються вони теж вздовж нормалі. Для різниці ходу променів дістанемо . (65.4)
. (65.4) , (65.5)
, (65.5) . (65.6)
. (65.6) . (65.7)
. (65.7) – порядковий номер кілець.
– порядковий номер кілець. і
і  . Тоді формула (65.7) набере вигляду:
. Тоді формула (65.7) набере вигляду: . (65.8)
. (65.8) , (65.9)
, (65.9)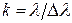 , тобто чим більша монохроматичність світла, тим більшу кількість максимумів можна спостерігати. Крім того, остання залежність дає змогу визначити смугу пропускання фільтра за допомогою вимірювання кількості видимих інтерференційних кілець:
, тобто чим більша монохроматичність світла, тим більшу кількість максимумів можна спостерігати. Крім того, остання залежність дає змогу визначити смугу пропускання фільтра за допомогою вимірювання кількості видимих інтерференційних кілець: . (65.10)
. (65.10)



