
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання 1. Ознайомлення із можливостями моделіСодержание книги
Поиск на нашем сайте
1. Змінюючи за допомогою “мишки” значення періоду кристалічної ґратки, спостерігати за зміною форми кривої розподілу кількості електронів, за положенням дифракційних максимумів та їх інтенсивністю. 2. Змінюючи за допомогою “мишки” значення швидкості електронів, що відповідає зміні значення прискорюючої напруги, проаналізувати зміну форми кривої розподілу кількості електронів, зміну положення дифракційних максимумів та їх інтенсивності. 3. За допомогою дебройлівської довжини хвилі, взятої з інтерфейсу, та формули (84.8) визначити гіпотетичне значення прискорюючої різниці потенціалів для електронного пучка. Завдання 2. Визначення періоду кристалічної ґратки 1. Встановити на інтерфейсі значення періоду кристалічної ґратки та швидкості електронів згідно Вашого варіанту із наведеної таблиці варіантів.
2. Виміряти (в наведених на екрані одиницях) відстані хп для кількох (3-5) дифракційних максимумів. 3. За допомогою формули (84.8) визначити значення періодів ґратки та знайти їх середнє значення. 4. Змінити значення швидкості (в два рази) і повторити п.п.1,2,3. 5. Порівняти отримані значення періоду із наведеними на екрані. Завдання 3. Визначення маси електрона 1. Для визначеного значення періоду кристалічної ґратки дослідити залежність хп(υ) для фіксованого значення п. Для цього на інтерфейсі встановити відповідне значення періоду кристалічної ґратки і, змінюючи значення швидкості електронів, провести виміри положення першого дифракційного максимуму. Дані занести в таблицю. 2. Користуючись отриманими даними, побудувати графік залежності хп(υ) в координатах хп(1/υ). Тоді ця залежність матиме вигляд:
3. Із графіка знайти коефіцієнт нахилу залежності хп(1/υ):
4. Користуючись отриманим експериментально значенням k та формулою (84.9), визначити масу електронів за допомогою формули:
5. Знайти похибки і порівняти отримане значення маси електрона із табличним. Контрольні запитання: 1. Які види випромінювання використовуються для дослідження кристалічної структури? 2. Сформулюйте закон Брегга. 3. В чому суть методу Лауе? 4. Охарактеризуйте метод обертання кристалу. 5. Опишіть суть методу порошку. 6. Коли для структурних досліджень методом дифракції застосовують електрони, а коли нейтрони? Література 1. Курик М.В., Цмось В.М. Фізика твердого тіла. Нав.посібник – К.: Вища школа, 1985, - 246 с. (Розділ 10). 2. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – 791 с. (Глави 2,3). 3. Лучицький Р.М., Галущак М.О. Фізика твердого тіла.Навч. пос.– Івано-Франківськ: Факел, 2008, – 250с. Додаткова література 4. Болеста І.М. Фізика твердого тіла. Навч. пос. – Львів: Видавн. центр ЛНУ імені Івана Франка.2003. – 480с. 5. Бушманов Б.Н., Хромов Ю.А. Фізика твердого тела: Уч. Пособие для вузов. – М.: Высшая школа, 1971. – 224 с. 6. Блейкмор Дж. Физика твердого тела / Пер. с англ. Под ред. Д.Т. Андрианова. – М.: Мир, 1988. – 608 с. 7. Епифанов Г.И. Физика твердого тела: Уч. Пособие. – Высшая школа, 1977. – 288 с.
В-85 Моделювання на ЕОМ проходження нейтронів через речовину Мета: визначити ймовірність проходження, поглинання і відбивання нейтрона, що проходить через пластинку, моделюванням процесу за методом Монте-Карло. Прилади і матеріали: програма комп’ютерної лабораторної роботи “Проходження нейтронів через пластинку”.
Теоретичні відомості Дж. Чедвік у 1932р. здійснив опромінення ізотопів
При захопленні ядром нейтрона з утворенням збудженого проміжного ядра швидкість вторинного нейтрона, який вилетів, значно менша, ніж швидкість захопленого первинного нейтрона. Оскільки первинні і вторинні нейтрони не можна розрізняти, таке явище сприймається як дещо вповільнене розсіяння нейтрона з втратою частини його енергії. Такий процес має назву непружного (резонансного) розсіяння частинок. У деяких випадках розпад проміжного збудженого ядра з випусканням ним вторинного нейтрона може затриматись настільки, що починає переважати конкуруючий процес – розпад ядер з випромінюванням γ-квантів під дією більш слабких електромагнітних сил. Після випускання γ-кванта збуджене ядро переходить в основний енергетичний стан. Такий процес взаємодії нейтрона з ядром називають радіаційним захопленням, який використовуються як для керування роботою реакторів за допомогою кадмієвих регулювальних стрижнів, так і для отримання в реакторах різних радіоактивних ізотопів. Із збільшенням енергії нейтронів збільшується спочатку ймовірність непружного розсіяння (n,n), а при енергіях в кілька МеВ мають місце реакції (n,p),(n, Слід мати на увазі, що при взаємодії нейтронів з речовиною завжди виконуються фундаментальні закони природи – збереження енергії та імпульсу. Задачу про проходження нейтронів через пластинку можна розв’язати, використовуючи метод Монте-Карло - чисельний метод розв’язування математичних задач за допомогою моделювання випадкових величин. Сама назва методу походить від назви міста Монте-Карло, відомого своїми гральними закладами, бо саме рулетка є найпростішим пристроєм для одержання випадкових величин. Щоб зрозуміти ідею методу Монте-Карло, достатньо розглянути приклад. Треба визначити площу довільної плоскої фігури, що розміщена всередині квадрата зі стороною рівною 1. Якщо вибрати всередині квадрата N випадково розміщених точок і підрахувати число точок N', які попали всередину описаної фігури, то площа фігури S буде рівна N'/N. Точність такого результату буде тим більша, чим більше число точок N буде взято. Методом Монте-Карло можна моделювати будь-який процес, на хід якого впливають випадкові факти. В деяких випадках зручно відмовитись від аналізу дійсного випадкового процесу і замість цього використати його модель. Саме так ми і зробимо, розглядаючи задачу про проходження потоку нейтронів через однорідну пластинку. Фізичні закони взаємодії окремої елементарної частинки з речовиною відомі. Треба знайти макроскопічні характеристики процесів, в яких бере участь велика кількість таких частинок. Нехай на нескінченну пластинку товщиною h падав нормально до неї потік нейтронів з енергією E0. Внаслідок зіткнення з ядрами атомів речовини, з якої складається пластинка, нейтрони можуть пружно розсіюватись чи поглинатись. Насправді взаємодія нейтронів із ядрами може приводити до різних результатів - пружного розсіювання, не пружного розсіювання, захоплення нейтрона ядром і поділ ядра на осколки. Однак для простоти ми будемо вважати, що відбуваються два – перший і третій із вказаних процесів і, більш того, припустимо, що енергія нейтрона при розсіюванні на ядрі не змінюється і будь-який напрямок поширення нейтрона від атома однаково ймовірний. Наше завдання - обчислити ймовірність проходження нейтрона скрізь пластинку РР, ймовірність поглинання нейтрона в пластинці РS і ймовірність його відбиття пластинкою РO. Дамо означення випадкової величини і ймовірності. Нехай ми проводимо послідовно q вимірювань над системою, причому щоразу вимірюємо одну і ту фізичну величину А. Позначимо через n(аi) кількість вимірювань, для яких вимірювана величина А має значення аi. Тоді ймовірність Р(аi) знаходження системи в стані, коли величина А має значення аi, дорівнює:
Звідси видно, що
Рівність (85.10) показує, що сумарна ймовірність того, що вимірювана величина має будь-яке із своїх можливих значень, дорівнює 1. Термін випадкова величина використовують тоді, коли хочуть підкреслити, що невідомо яким виявиться конкретне значення цієї фізичної величини при одноразовому вимірюванні. Однак нам може бути відомо, які значення вона може приймати і які ймовірності їх реалізації. Тому, щоб задати випадкову величину треба вказати, які значення вона може приймати і які їх ймовірності. Наведені поняття ймовірності і випадкової величини дають змогу означити середнє значення або математичне сподівання будь-якої фізичної величини А:
Це стосується випадкової величини, що приймає дискретні значення. Для неперервної випадкової величини, яка задається інтервалом можливих значень і густиною ймовірності р(х), що має бути більша за 0, формули (85.10) і (85.11) мають вигляд:
Легко встановити зміст густини ймовірності р(х). Очевидно, що
рівна ймовірності того, що величина х має значення з інтервалу (а`, b`). В нашій задачі взаємодія нейтронів із речовиною характеризується двома сталими Між двома послідовними зіткненнями з ядрами атомів речовини пластинки нейтрон проходить деякий шлях, який називається довжиною вільного пробігу і позначається
Умова нормування (85.12) виконується, бо
З формули (85.14) можна знайти вираз для середнього значення:
Тепер слід вибрати певний спосіб моделювання випадкової величини
Вибравши значення
а друге рівняння (85.16) дає формулу для розігрування
Тепер залишається вибрати випадковий напрям руху нейтрона після розсіювання. Оскільки в моделі, що розглядається, є симетрія відносно осі х, то цей напрям повністю визначається одним кутом Вимога однакової ймовірності будь-якого напряму в цьому випадку рівносильна вимозі, щоб величина
Оскільки а = -1, b = 1, то формула набуде вигляду: Складемо схему розрахунку ймовірностей РР, РS, РО шляхом моделювання дійсних траєкторій. Припустимо, що нейтрон зазнав k розсіяння всередині пластинки в точці з абсцисою хk і після цього рухається в напрямі
і обчислимо абсцису наступного зіткнення нейтрона з ядром
Якщо виявиться, що хi>h, то нейтрон покинув пластинку, рахунок траєкторій нейтрона закінчується і додається одиниця до лічильника частинок, які пройшли через пластинку. В іншому випадку перевіряємо умову виходу нейтрона із пластинки назад: хk+1<0. Якщо ця умова виконується, то рахунок траєкторій закінчується і додається 1 до лічильника частинок, що відбились. Якщо і ця умова не виконується, тобто 0<хk+1<b, то нейтрон зазнає ще одного, k+1 зіткнення всередині пластинки і слід визначити "долю " нейтрона при цьому (k+1) зіткненні. Вибираємо чергове значення
Якщо ця нерівність виконана, то підрахунок траєкторій закінчується і до лічильника поглинутих частинок додається 1. В іншому випадку приймаємо, що нейтрон розсіявся в точці з абсцисою хk+1. Виберемо новий напрямок швидкості нейтрона. У відповідності з (85.18) маємо: Кожна траєкторія нейтрона характеризується початковими значеннями Хo=0 і
Інтерфейс програми “Дослід Резерфорда”
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.117.237 (0.012 с.) |

 . (84.9)
. (84.9)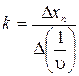 . (84.10)
. (84.10) . (84.11)
. (84.11) Ве
Ве - частинками. В результаті цієї ядерної реакції утворюються частинки з масою 1,674926 10-27 кг, яка близька до маси протона. Ці частинки назвали нейтронами. У вільному стані нейтрон нестабільний – середній час існування становить 12,5 хв. Подібність нейтрона за цілим рядом ознак до протона дає підставу вважати, що вони є двома квантовими станами (ізоспіновим дублетом) однієї частинки, яка називається нуклоном і є складовою частиною атомного ядра. Оскільки нейтрони, на відміну від позитивно заряджених протонів, є електронейтральними, то при бомбордуванні ними атомних ядер не існує потенціального бар’єру. Тому після відкриття нейтронів їх почали широко використовувати для проведення ядерних реакцій. Такі ядерні реакції з участю нейтронів мають велике практичне застосування. Ряд наймасивніших ядер (
- частинками. В результаті цієї ядерної реакції утворюються частинки з масою 1,674926 10-27 кг, яка близька до маси протона. Ці частинки назвали нейтронами. У вільному стані нейтрон нестабільний – середній час існування становить 12,5 хв. Подібність нейтрона за цілим рядом ознак до протона дає підставу вважати, що вони є двома квантовими станами (ізоспіновим дублетом) однієї частинки, яка називається нуклоном і є складовою частиною атомного ядра. Оскільки нейтрони, на відміну від позитивно заряджених протонів, є електронейтральними, то при бомбордуванні ними атомних ядер не існує потенціального бар’єру. Тому після відкриття нейтронів їх почали широко використовувати для проведення ядерних реакцій. Такі ядерні реакції з участю нейтронів мають велике практичне застосування. Ряд наймасивніших ядер ( U,
U, 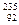 U,
U, 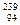 Pu) стають нестабільними при захопленні ними нейтронів і зазнають поділу з виділенням великої кількості енергії. Такі ядерні реакції лежать в основі роботи ядерних реакторів на повільних нейтронах, які функціонують на АЕС.
Pu) стають нестабільними при захопленні ними нейтронів і зазнають поділу з виділенням великої кількості енергії. Такі ядерні реакції лежать в основі роботи ядерних реакторів на повільних нейтронах, які функціонують на АЕС.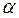 ). Такі реакції, як і реакції
). Такі реакції, як і реакції  радіаційного захоплення, обумовлюють утворення β-активних ядер. На відміну від приведених ядер, які зазнають поділу під дією повільних нейтронів, ядра
радіаційного захоплення, обумовлюють утворення β-активних ядер. На відміну від приведених ядер, які зазнають поділу під дією повільних нейтронів, ядра  U,
U,  Th зазнають поділу тільки під дією швидких нейтронів, енергія яких досягає кілька МеВ. На таких реакціях ґрунтується робота реакторів на швидких нейтронах. При енергії нейтронів (10
Th зазнають поділу тільки під дією швидких нейтронів, енергія яких досягає кілька МеВ. На таких реакціях ґрунтується робота реакторів на швидких нейтронах. При енергії нейтронів (10  20) МеВ можливі реакції (n,2n), а при енергіях (20
20) МеВ можливі реакції (n,2n), а при енергіях (20  С. Нейтронні потоки широко застосовуються при каротажу нафтових свердловин, оскільки використовується залежність прониклої здатності нейтронів від роду матеріалів земної породи.
С. Нейтронні потоки широко застосовуються при каротажу нафтових свердловин, оскільки використовується залежність прониклої здатності нейтронів від роду матеріалів земної породи. . (85.9)
. (85.9) . (85.10)
. (85.10)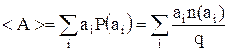 . (85.11)
. (85.11)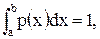 (85.12)
(85.12) (85.13)
(85.13)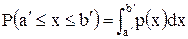
 і
і  , які називаються перерізом поглинання і перерізом розсіяння. Сума
, які називаються перерізом поглинання і перерізом розсіяння. Сума  називається повним перерізом. Фізичний зміст перерізів такий: внаслідок зіткнення нейтрона із атомом речовини ймовірність поглинання дорівнює
називається повним перерізом. Фізичний зміст перерізів такий: внаслідок зіткнення нейтрона із атомом речовини ймовірність поглинання дорівнює 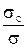 , а ймовірність розсіяння дорівнює
, а ймовірність розсіяння дорівнює 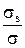 .
. . Довжина вільного пробігу - це випадкова величина, яка може приймати будь-яке додатне значення. Густина ймовірності для
. Довжина вільного пробігу - це випадкова величина, яка може приймати будь-яке додатне значення. Густина ймовірності для  .
. . (85.14)
. (85.14) (85.15)
(85.15) , рівномірно розподілена в інтервалі (0,1). Процес знаходження значення якоїсь випадкової величини х шляхом перетворень одного чи декількох значень
, рівномірно розподілена в інтервалі (0,1). Процес знаходження значення якоїсь випадкової величини х шляхом перетворень одного чи декількох значень  або
або  . (85.16)
. (85.16) величини х. Для даного випадку згідно (85.14), враховуючи, що
величини х. Для даного випадку згідно (85.14), враховуючи, що  ,
, . (85.17)
. (85.17) між напрямом швидкості нейтрона і віссю х.
між напрямом швидкості нейтрона і віссю х. була рівномірно розподілена в інтервалі (-1, 1), оскільки
була рівномірно розподілена в інтервалі (-1, 1), оскільки  . Іншими словами р(х) = С. З виразу (85.12) знаходимо С=1/(b-а), і тоді перше із рівнянь (85.16) набуває вигляду:
. Іншими словами р(х) = С. З виразу (85.12) знаходимо С=1/(b-а), і тоді перше із рівнянь (85.16) набуває вигляду: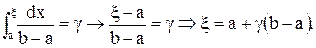 (85.18)
(85.18)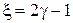 .
. . Визначимо довжину вільного пробігу нейтрона, вибравши значення
. Визначимо довжину вільного пробігу нейтрона, вибравши значення  :
: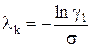
 (85.19)
(85.19)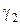 і перевіряємо умову поглинання
і перевіряємо умову поглинання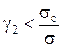 . (85.20)
. (85.20) і повторюємо весь цикл заново, але вже з іншими значеннями
і повторюємо весь цикл заново, але вже з іншими значеннями  . Після того, як будуть підраховані N траєкторій, виявиться, що Np нейтронів пройшли крізь пластинку, Ns нейтронів були поглинуті, No – нейтронів – відбиті. Шукані ймовірності обчислюються за формулами:
. Після того, як будуть підраховані N траєкторій, виявиться, що Np нейтронів пройшли крізь пластинку, Ns нейтронів були поглинуті, No – нейтронів – відбиті. Шукані ймовірності обчислюються за формулами: (85.21)
(85.21)



