
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
І.Фізичні вимірювання та похибки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Фізичні вимірювання поділяються загалом на прямі та посередні (непрямі). Прямі вимірювання - вимірювання фізичних величин за допомогою засобів вимірювання (приладів), які дозволяють безпосередньо знаходити значення вимірюваної величини шляхом порівняння з мірою – вторинним еталоном, або за шкалою приладу. Наприклад, масу вимірюють на терезах, довжину - лінійкою, штангенциркулем, час - секундоміром та інше. Посередні вимірювання - визначення значення фізичної величини через перерахунок значень відповідних величин, які знаходяться прямими вимірюваннями. Наприклад, об'єм циліндра визначається через величини діаметра основи d та висоти h, опір провідника знаходимо через значення струму І і падіння напруги U та інше. Якість будь-якого вимірювання визначається величиною похибки вимірювання, яка фактично задає межі оцінки. Похибкою вимірювання називаємо різницю між істиним і виміряним значенням фізичної величини
При прямих вимірюваннях похибка визначається класом точності приладу, методом вимірювання (послідовністю дій та операцій), а також відтворюваністю результатів вимірювання. У посередніх вимірюваннях результуюча похибка визначається похибками результатів прямих вимірювань та структурою формул (математичною моделлю) їх перерахунку у результат посереднього вимірювання. за характером появи похибки вимірювання поділяються на випадкові та систематичні. Випадкові похибки - це похибки, що непередбачувано змінюють свою величину та знак при повторних вимірах. Вони певним чином пов'язані із суб'єктом дослідника та властивостями об'єкта вимірювання. Наприклад, значення довжини предмета, що вимірюється, можна оцінити, дивлячись на шкалу лінійки злівого чи правого боку від поділки, яка співпадає із границею предмета. У цьому прикладі результати вимірювання довжини предмету будуть різні, а величина похибки - пропорційна товщині лінійки. Виключення випадкових похибок принципово неможливе, але якщо у вимірюваннях є повторюваність – тобто істине значення фізичної величини існує і є найбільшімовірним, і якщо за результат вимірювання приймається середньоарифметичне значення
При симетричному Гаусовому розподілі
Сама похибка вимірювання оцінюється її середньоквадратичним значенням
Тобто, збільшуючи кількість повторних вимірювань Сказане справедливе при умові, що кількість повторних вимірювань досить велика; досвід стверджує, що має бути Систематичні похибки - похибки, що зберігають в процесі вимірювання свою величину і знак або змінюються за відомим законом. Вони найчастіше пов'язані з похибками приладів, методикою вимірювання і обмеженістю математичної моделі явища, коли не враховуються в повній мірі його характеристики. Наприклад, помилки при градуюванні шкали приладу, вимірювання приладами за граничними межами умов їх застосування та інше. Систематичні похибки виявляють, використовуючи метод заміщення вимірюваної величини відомою - еталоном, інші (більш точні) засоби вимірювання або інші методи вимірювання. Виявлена в такий спосіб систематична похибка може бути виключена із результату вимірювання (корекція похибок), але не повністю. Адже і більш точним приладам та досконалим методам вимірювання притаманні властиві їм похибки. Оцінюючи характер випадкових та систематичних похибок можна зробити такий висновок: при наявності випадкових похибок результати вимірювання коливаються біля істинного значення вимірюваної величини, а при наявності систематичних похибок - біля значення вимірюваної величини, зміщеного на величину систематичної похибки. За джерелом виникнення похибок вимірювання їх поділяють на методичні та інструментальні, перші з яких, як вже згадувалось вище, зумовлені методикою вимірювання і обмеженістю математичної моделі явища, що не враховує в повній мірі його характеристики, а друга - похибками приладів, помилками при градуюванні шкали, вимірюванням за граничними межами умов їх застосування. При опрацюванні результатів вимірювань у лабораторному практикумі в якості систематичної похибки виступає інструментальна похибка: величина цієї похибки наводится в нормативній документації на засіб вимірювання (паспорт, технічні умови, стандарти), або її визначаємо за величиною ціни поділки шкали приладу, а саме, не менше ±0,5 від ціни поділки. Наприклад, якщо якомусь тілу надписом задана його маса: m=1650 г, то похибка визначення маси становить ±1 грам. Або, якщо на лінійці нанесені міліметрові поділки, то інструментальна похибка не може бути меншою за ±0,5 мм.
Одночасно вважається, що розроблена і застосована методика вимірювань дозволяє врахувати і оцінити значущі похибки та знехтувати іншими систематичними похибками через їх незначущість, через що виявляється мінімізованою і методична похибка. існують певні теоретичні підходи до статистичної обробки результатів вимірювань, за допомогою яких оцінка результатів вимірювання враховує відповідний баланс випадкових та систематичних похибок. Цей баланс визначає міру надійності отриманих результатів та висновків. При опрацюванні результатів вимірювання у лабораторному практикумі і обмеженій величиною 5-15 кількості послідовних вимірів можуть бути безпосередньо застосовані вирази [1.1-4.1] для оцінки похибки вимірювання і її достовірності, а для перевірки того, як можуть змінитись ці оцінки при повторних вимірах в тих же умовах, визначають довірчий інтервал істиного значення виміряної величини. довірчий інтервал істиного значення виміряної величини є такий інтервал, який із заданою імовірністю, названою «довірчою», накриває (включає) істине значення виміряної величини. Найчастіше довірчі інтервали визначають, спираючись на розподіл Ст'юдента – розподіл випадкової величини такого вигляду
де: Довірчий інтервал
де, α - рівень значущості, Р=1-α – довірча імовірність. Принцип знаходження довірчого інтервалу пояснюється на Рис.1.0.
Для функции розподілу Гауса повна імовірність дорівнює
Для довірчої імовірності справедливо
Це означає, що істине значення виміряної величини знаходиться у довірчому інтервалі із заданою довірчою імовірністю. У фізичному експерименті найчастіше приймають довірчу імовірність Рα,n=0,95 або Рα,n=0,99. Із використанням розподілу Ст'юдента оцінку виміряного значення фізичної величини записують в такий спосіб
Використання наведеної вище схеми передбачає умову, що вимірювані величини підкоряються розподілу Гауса, проте на практиці це підтверджувати немає потреби, тому що реальні розподіли, за звичай, обмежені-«урізані» і розподіл Ст'юдента «перекриває» їх. Для заданої довірчої імовірності Рα,n і кількості вимірів n величина коефіцієнта Ст'юдента tα,n розрахована через інтеграл (7.0) і протабульована (див.Таблицю1.0). Правила скруглювання. При записі виміряного значення А, останньою повинна записуватися цифра того десяткового розряду, який використано при записі границі довірчого інтервалу. Це правило слід застосовувати і в тому випадку коли деякі цифри є нулями. Наприклад, в результаті m= 0.900 ± 0.004 в числі 0.900 потрібно писати нулі. Запис 0.9 означав би, що про наступні значущі цифри нічого невідомо, хоч вимірювання показали, що вони рівні нулю. Аналогічно, якщо m=5.3 кг (із точністю до десятих кг), то запис m=5300 г означає, що вимірювання проведені з точністю до грамів. Якщо ж потрібно записати масу в грамах, то це потрібно зробити так: m=5.3·103 г. При записі границі довірчого інтервалу, її значення слід округляти до двох значущих, якщо перша з них одиниця, і до одної значущої цифри у всіх інших випадках. Так, правильно писати ±3, ±0.2, ±0.08, ±0.14 і не слід писати ±3.2, ±0.23, ±0.084. Не слід скругляти ±0.14 до ±0.1. Пояснимо це правило. Похибку експерименту рідко вдається визначити з точніше як у 20%. Якщо похибку визначено як 0.14, то округлення 0.14 до 0.1 змінює величину похибки на 40%, в той час як округлення 5 чисел 0.26 і 3.4 до 0.3 змінює похибку менше ніж на 15%, що не дуже суттєво.
Таблиця 1.0
Для випадку посередніх вимірювань результуюча похибка буде визначатись, вочевидь, через похибки складових-аргументів, які були знайдені шляхом прямих вимірів. Вимірювана величина А визначається через незалежно визначені складові-аргументи
де,
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.250.18 (0.012 с.) |

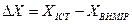 (1.0)
(1.0)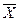 кількох (
кількох (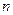 ) послідовних вимірювань
) послідовних вимірювань 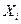 , то похибки в значній мірі компенсуються.
, то похибки в значній мірі компенсуються. . (2.0)
. (2.0)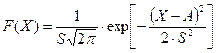 значень вимірюваної величини
значень вимірюваної величини 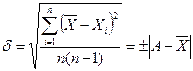 . (3.0)
. (3.0)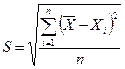 . (4.0)
. (4.0)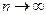 , при умові стаціонарності процесу, можна зменшити випадкову похибку до будь-якої малої величини.
, при умові стаціонарності процесу, можна зменшити випадкову похибку до будь-якої малої величини.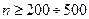 , в залежності від характеру вимірюваної величини.
, в залежності від характеру вимірюваної величини.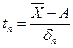 . (5.0)
. (5.0)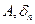 - оцінка істиного значення і нескомпенсований залишок відповідно для n вимірів.
- оцінка істиного значення і нескомпенсований залишок відповідно для n вимірів.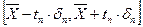 в цьому випадку відповідає імовірності
в цьому випадку відповідає імовірності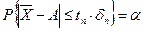 . (6.0)
. (6.0)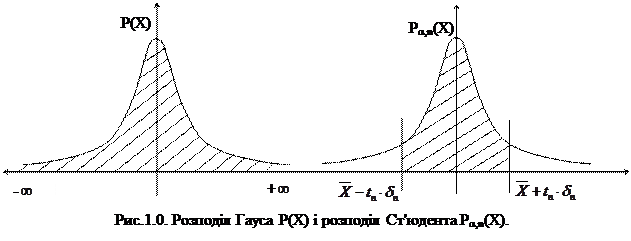
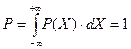 .
.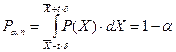 . (7.0)
. (7.0)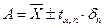 . (8.0)
. (8.0)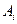 , тому і складові результуючої похибки також будуть незалежні, або, як кажуть, між ними відсутня кореляція. При такій умові результуючу похибку можна ототожнити з багатоскладовим вектором, квадрат модуля якого дорівнюватиме суммі квадратів складових. Якщо говорити про дисперсії складових-аргументів
, тому і складові результуючої похибки також будуть незалежні, або, як кажуть, між ними відсутня кореляція. При такій умові результуючу похибку можна ототожнити з багатоскладовим вектором, квадрат модуля якого дорівнюватиме суммі квадратів складових. Якщо говорити про дисперсії складових-аргументів 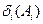 , то результуючу дисперсію
, то результуючу дисперсію 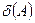 можна визначити таким виразом
можна визначити таким виразом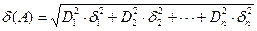 . (9.0)
. (9.0)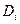 - коефіцієнти впливу складових, які визначаються через частинні похідні від вимірюваної величини-функції по складових-аргументах:
- коефіцієнти впливу складових, які визначаються через частинні похідні від вимірюваної величини-функції по складових-аргументах: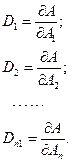 (10.0)
(10.0)


