
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання 2. Визначення величини моменту інерції тіла в залежності від його положення відносно вісі обертання.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Увага! Завдання 2 виконується виключно під орудою викладача або майстра виробничого навчання(лаборанта).
В якості досліджуваних тіл (Рис.3.4) використовуються спеціальні тіла, які мають відповідні конструктивні елементи (отвори), що дозволяє закріплювати їх в рамці в різних положеннях. · Закріпити в рамці маятника досліджуване тіло; · Виконати вимірювання за п.п.2.2; · Результати вимірювань занести в Таблицю 1; · Визначити значення моменту інерції тіла JХ за формулою (9.4), прийнявши значення J0 – величину моменту інерції рамки, знайдене при виконанні Завдання 1; · Довірчі межі найбільшімовірних значень моменту інерції тіла визначаємо за формулою
·
· Теорему Штайнера можна вважати справедливою, якщо при зміщенні центру мас досліджуваного тіла на відстань а відносно вісі обертання маятника, між визначеним значенням моменту інерції J(а) і величиною а2 буде спостерігатись лінійна кореляція (Рис.4.4.). обробка результатів вимірювання може бути виконана із застосуваням програмних систем Excel, Мсad, ORIGIN та інш.; прикладвикористанняМсad для знаходження величини прискорення вільного падіння наведений в методичному посібнику [5.4]. Контрольні питання 1. Виведіть із рівняння Ньютона рівняння коливань крутильного маятника
2. Виведіть формулу для визначення моменту інерції циліндричного кільця
3. Виведіть формулу для визначення моменту інерції кулі
4. Виведіть рівняння для визначення моменту інерції досліджуваного тіла, із застосуванням крутильного маятника.
ЛІТЕРАТУРА 1.4. Кучерук І.М., Горбачук І.Т., Луцик П.П.. Загальний курс фізики: Навчальний посібник. –Т. 1.: Механіка. Молекулярна фізика і термодинаміка. – К.: Техніка, 1999. – 536 с. 2.4. Дущенко В.П., Кучерук І.М. Загальна фізика. Фізичні основи механіки. Молекулярна фізика і термодинаміка. – К.: Вища школа, 1993. – 431 с. 3.4. Загальна фізика. Лабораторний практикум: Навч. посібник за заг.ред. І.Т. Горбачука. – К.: Вища школа, 1992. – 509 с. 4.4. Трофимова Т.И. Курс физики. – М.: Высш. шк., 2000. – 478 с. 5.4. Опрацювання результатів вимірювання при виконанні лабораторних робіт фізичного практикума з використанням математичної системи Mcad. (Методичні вказівки до лабораторного практикуму для студентів усіх спеціальностей). А.О.Потапов, А.І.Мотіна. - К.: КНУТД, 2004.- 112 с.
Лабораторна робота № 40
Вимірювання прискорення сили тяжіння За допомогою математичного маятника Мета роботи · визначити величину прискорення сили тяжіння Землі. Теоретичні відомості.
Величину моменту сили тяжіння можна записати у вигляді
де J=mL2 ¾ момент інерції точкового тіла. Вектори
В канонічному вигляді це рівняння має вигляд:
де Таким чином, період власних коливань визначається так
У цьому виразі g ¾ прискорення сили тяжіння Землі або як кажуть прискорення вільного падіння. Із закону всесвітнього тяжіння Ньютона можна показати що
g=9,8 м/с2. З формули (1) випливає, що залежність довжини маятника L від періоду коливань T можна записати так
Якщо покласти
то вираз (3) можна лініаризувати
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.43.27 (0.052 с.) |

 При відомому значенні моменту інерції рамки маятника, рамку можна використовувати в якості пробного тіла і знаходити моменти інерції інших тіл, що можуть бути закріплені в рамці, за формулою (9.4).
При відомому значенні моменту інерції рамки маятника, рамку можна використовувати в якості пробного тіла і знаходити моменти інерції інших тіл, що можуть бути закріплені в рамці, за формулою (9.4).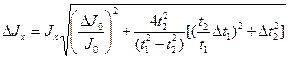 .
.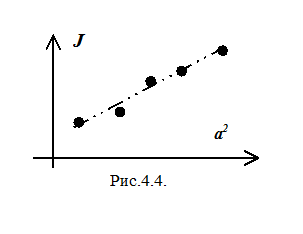 Змінюючи положення досліджуваного тіла в рамці відносно вісі обертання можна перевірити справедливість теореми Штайнера, яка стверджує, що момент інерції тіла J(а) відносно вісі, що паралельна тій, яка проходить через центр мас тіла і знаходиться від неї на відстані а, дорівнює сумі величини момента інерції тіла відносно вісі, яка проходить через центр мас, і добутку маси М цього тіла на квадрат відстані від цієї вісі
Змінюючи положення досліджуваного тіла в рамці відносно вісі обертання можна перевірити справедливість теореми Штайнера, яка стверджує, що момент інерції тіла J(а) відносно вісі, що паралельна тій, яка проходить через центр мас тіла і знаходиться від неї на відстані а, дорівнює сумі величини момента інерції тіла відносно вісі, яка проходить через центр мас, і добутку маси М цього тіла на квадрат відстані від цієї вісі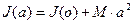 .
.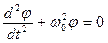 і формулу для періоду коливань
і формулу для періоду коливань  .
.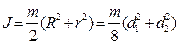 .
.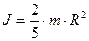 .
.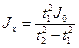 .
.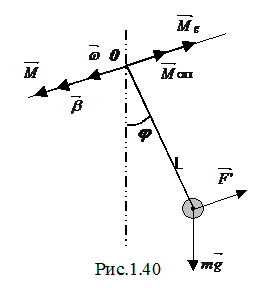 Математичний маятник (Рис.1.40) ¾ точкове тіло масою m, підвішене на нерозтяжному підвісі L, розмірами якого, порівнюючи з довжиною підвісу, можна знехтувати. Маса підвісу значно менша маси тіла m. Коливання описуються кутом відхилення тіла від положення рівноваги ¾
Математичний маятник (Рис.1.40) ¾ точкове тіло масою m, підвішене на нерозтяжному підвісі L, розмірами якого, порівнюючи з довжиною підвісу, можна знехтувати. Маса підвісу значно менша маси тіла m. Коливання описуються кутом відхилення тіла від положення рівноваги ¾ 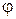 . Вектор
. Вектор 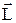 задає точку прикладання сил. Коливання здійснюються в загальному випадку під дією моменту
задає точку прикладання сил. Коливання здійснюються в загальному випадку під дією моменту 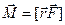 зовнішніх сил
зовнішніх сил 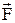 , моменту сили тяжіння
, моменту сили тяжіння  та моменту сил опору
та моменту сил опору 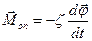 , де
, де  ¾ коефіцієнт опору. Вектори моментів сил
¾ коефіцієнт опору. Вектори моментів сил  та кутового прискорення
та кутового прискорення  лежать на осі обертання, яка ^ площині коливання та проходить через центр обертання О.
лежать на осі обертання, яка ^ площині коливання та проходить через центр обертання О. . Для малих коливань j маємо sinj» j і
. Для малих коливань j маємо sinj» j і  . За другим законом Ньютона рівняння коливань можна записати так
. За другим законом Ньютона рівняння коливань можна записати так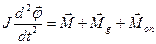 ,
, лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній, векторне рівняння можна записати в алгебраїчній формі
лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній, векторне рівняння можна записати в алгебраїчній формі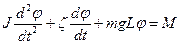 .
.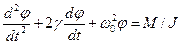 ,
,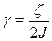 ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань,  , w0 ¾ частота вільних незгасаючих коливань, або частота власних коливань маятника.
, w0 ¾ частота вільних незгасаючих коливань, або частота власних коливань маятника. . (1.40)
. (1.40)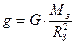 , (2.40)
, (2.40)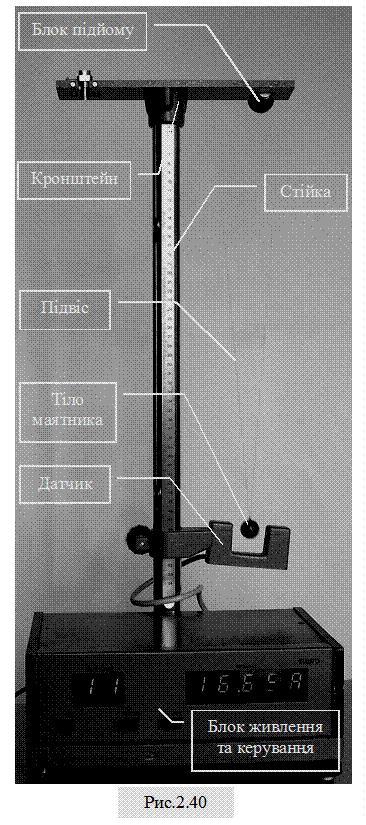 де GЗ=6,67×1011 Н×м2/кг2 – гравітаційна стала, МЗ=5б976×1024 кг ¾ маса Землі, RЗ=6,4×106 м ¾ радіус Землі, L ¾ довжина підвісу маятника. Підрахунок за формулою (2) дає величину прискорення сили тяжіння рівною
де GЗ=6,67×1011 Н×м2/кг2 – гравітаційна стала, МЗ=5б976×1024 кг ¾ маса Землі, RЗ=6,4×106 м ¾ радіус Землі, L ¾ довжина підвісу маятника. Підрахунок за формулою (2) дає величину прискорення сили тяжіння рівною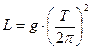 (3.40)
(3.40) , (4.40)
, (4.40)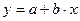 . (5.40)
. (5.40)


