
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вільні осі. Головні осі інерції. Моменти інерції різних тілСодержание книги
Поиск на нашем сайте
При обертанні тіла навколо довільно обраної осі в загальному випад-ку вісь обертання або повертається, або переміщується відносно умовно не-рухомої системи відліку. Для того, щоб така вісь обертання залишалася в незмінному положенні, до неї необхідно прикласти певні зовнішні сили. При обертанні однорідного симетричного тіла вісь обертання збері-гала б своє положення в просторі без впливу на неї ззовні. Вісь обертання тіла, положення якої в просторі зберігається без дії на неї будь-яких сил ззовні, називають вільною віссю тіла. Для тіла будь-якої форми і з будь-яким розподілом маси існує три вза-ємно перпендикулярні осі, що проходять через центр інерції тіла, які мо-жуть служити вільними осями – їх називають головними осями інерції. У загальному випадку головні осі інерції тіла можуть бути обрані не в будь-якому довільному напрямку, а лише в певному, тобто вони фіксовані. В од-норідного тіла із площинною симетрією (наприклад, паралелепіпеда) фіксо-вані дві головні осі інерції. В однорідного тіла з осьовою симетрією (напри-клад, циліндра) фіксована лише одна з головних осей інерції (вісь цилінд-ра). В однорідного тіла із центральною симетрією (кулі) жодна з головних осей інерції не фіксована. Моменти інерції відносно головних осей називають головними мо-ментами інерції тіла
Для тіла з осьовою симетрією два головні моменти інерції мають однакову величину, а третій відмінний від них:
Момент інерції тіла описується рівнянням (7.26). Масу речовини Δ mi можна виразити через густину речовини ρ і об'єм
Тут вираз Δ V →0 означає, що об'єм стягується до тієї точки тіла, де визначається густина ρ, але Δ V ≠0, а обмежується деяким мінімальним об'ємом, у межах якого можна говорити про густину речовини. Таким чи-ном, враховуючи (7.31), величину моменту інерції можна виразити рів-нянням:
Сума (7.32) тим точніша, чим менші Δ Vi. Отже, завдання знаходження мо-ментів інерції зводиться до обчислення інтеграла виду:
Для однорідних за густиною тіл
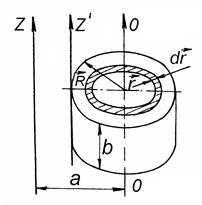
Рис.7.8 Для визначення моменту інерції відносно осі z' скористаємося теоремою Штейнера: момент інерції
(З доведенням теореми Штейнера можна ознайомитись за посібником [1]). Вісь z' відстоїть від осі ОО на відстані
7.6.2. Момент інерції товстостінного циліндра з порожниною відносно головної осі інерції.
Тут R 1 й R 2 – внутрішній і зовнішній радіуси циліндра відповідно:
Тоді: 7.6.3. Головний момент інерції тонкостінного циліндра. Для тонкостінного циліндра можна прийняти, що
7.6.4. Момент інерції матеріальної точки m відносно довільної осі обертання z, що відстоїть на відстані
Рис.7.9 Тут L – довжина стержня. Згідно з теоремою Штейнера момент інерції стержня відносно осі z дорівнює:
7.6.6. Момент інерції тонкого диска відносно осі, що співпадає з діаметром диска. Елементарний момент інерції
7.6.7. Головний момент інерції кулі. Для однорідної кулі
Рис. 7.10 Рис. 7.11
І для диска, і для кулі
Розглянемо обертальний рух тіла відносно закріпленої точки О, котра співпадає з початком інерціальної системи відліку (рис 7.12). Проведемо через точку О миттєву вісь ОА. Нехай Рис.7.12.
Момент імпульсу всього тіла
Всі частинки тіла мають одну й ту саму кутову швидкість
Оскільки
Подібні рівняння можна записати для
Кожен із цих коефіцієнтів залежить від миттєвої орієнтації тіла від-носно осей координат
Аналогічно можна записати коефіцієнти для проекцій
Сукупність дев’яти величин
називають тензором інерції тіла відносно точки О, а самі ці величини – компонентами цього тензора, або компонентами матриці (див. [4] та [5]).Сукупність рівнянь (7.36) вказує на те, що у випадках тіл довільної форми з довільним розподілом маси момент імпульсу Величини Якщо
Очевидно, що сума діагональних компонентів
На підставі рівняння (7.38) обчислимо головний момент інерції однорідної кулі радіуса
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.009 с.) |

 . У загальному випадку ці моменти різні:
. У загальному випадку ці моменти різні:
 . Для тіла із цен-тральною симетрією всі три головні моменти інерції однакові:
. Для тіла із цен-тральною симетрією всі три головні моменти інерції однакові:
 . Густина речовини в будь-якій точці виражається співвідношенням:
. Густина речовини в будь-якій точці виражається співвідношенням: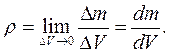 (7.31)
(7.31)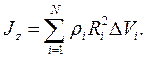 (7.32)
(7.32)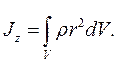 (7.33)
(7.33)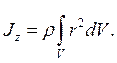
 Розглянемо кілька окремих прикладів роз-рахунку моментів інерції однорідних симетричних тіл.
Розглянемо кілька окремих прикладів роз-рахунку моментів інерції однорідних симетричних тіл. 7.6.1. Момент інерції циліндра. Відносно головної осі інерції ОО (рис.7.8) момент інерції
7.6.1. Момент інерції циліндра. Відносно головної осі інерції ОО (рис.7.8) момент інерції
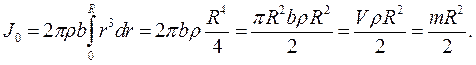
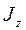 відносно довіль-ної осі z, паралельної головній осі інерції, дорівнює сумі головного моменту інерції
відносно довіль-ної осі z, паралельної головній осі інерції, дорівнює сумі головного моменту інерції  між осями:
між осями: (7.34)
(7.34) . Тоді момент інерції циліндра відносно осі z' дорівнює:
. Тоді момент інерції циліндра відносно осі z' дорівнює: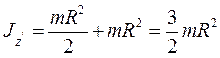 .
.
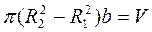 – об’єм пустотілого циліндра.
– об’єм пустотілого циліндра.
 і
і  , і
, і
 .
. 7.6.5. Момент інерції тонкого довго-го стержня з постійним перетином S будь-якої форми. Елемент об'єму dV стержня при обертанні його навколо головної осі інерції ОО (рис. 7.9) дорівнює
7.6.5. Момент інерції тонкого довго-го стержня з постійним перетином S будь-якої форми. Елемент об'єму dV стержня при обертанні його навколо головної осі інерції ОО (рис. 7.9) дорівнює 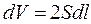 . Тоді
. Тоді
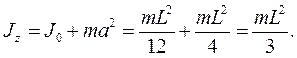
 (рис.7.10). За умови, що товщина диска
(рис.7.10). За умови, що товщина диска  , момент інерції диска від-носно осі Z знайдемо за рівнянням:
, момент інерції диска від-носно осі Z знайдемо за рівнянням: 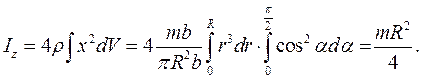
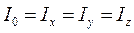 . Елементарний момент інерції
. Елементарний момент інерції 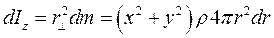 (рис. 7.11). Згідно з теоремою Піфагора
(рис. 7.11). Згідно з теоремою Піфагора  . Сферична система симетрична, і середні значення
. Сферична система симетрична, і середні значення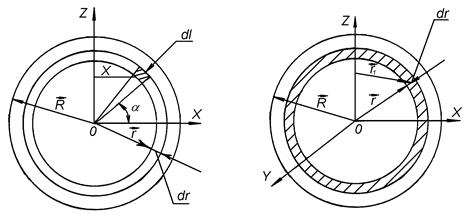
 . Прийнявши, що
. Прийнявши, що  , знаходимо:
, знаходимо: .
.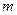 – маса однорідного тіла, ρ – густина речовини.
– маса однорідного тіла, ρ – густина речовини. 7.7. Тензор інерції
7.7. Тензор інерції – миттєва кутова швидкість тіла відносно ціеї осі. Момент імпульсу
– миттєва кутова швидкість тіла відносно ціеї осі. Момент імпульсу  частинки
частинки  цього тіла відносно точки О:
цього тіла відносно точки О: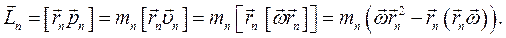


 то
то
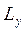 та
та 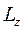 . Останнє рівняння має три коефіцієнти:
. Останнє рівняння має три коефіцієнти:
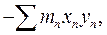
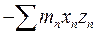 .
. . Їх називають інерціальними коефіцієнтами або моментами інерції:
. Їх називають інерціальними коефіцієнтами або моментами інерції: (7.35)
(7.35) (7.36)
(7.36)

 (7.37)
(7.37) не є простим добутком скаляра
не є простим добутком скаляра  на вектор
на вектор 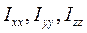 називають діагональними компонентами тензора, а всі інші – недіагональними. Вони симетричні:
називають діагональними компонентами тензора, а всі інші – недіагональними. Вони симетричні:  . Діагональні компоненти, наприклад
. Діагональні компоненти, наприклад 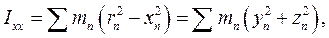 є сумою добутків кожної маси на квадрат її відстані від осі обертання, тому їх називають моментами інерції відносно осі.
є сумою добутків кожної маси на квадрат її відстані від осі обертання, тому їх називають моментами інерції відносно осі. – густина тіла в точці, радіус-вектор якої є
– густина тіла в точці, радіус-вектор якої є  , то кожен мо-мент інерції можна записати у вигляді інтегралів, наприклад:
, то кожен мо-мент інерції можна записати у вигляді інтегралів, наприклад: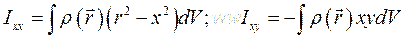 .
. (7.38)
(7.38) , мас якої
, мас якої 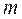 :
: що співпадає з результатами (7.6.7).
що співпадає з результатами (7.6.7).


