
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон всесвітнього тяжіння. Вільне падіння тілСодержание книги
Поиск на нашем сайте
У результаті узагальнення численних спостережень, експерименталь-них і теоретичних досліджень (як своїх власних, так й інших дослідників) І.Ньютон в 1687 р. сформулював закон всесвітнього тяжіння: „Кожні дві матеріальні частинки притягують одна іншу із силою
Сила У векторній формі закон всесвітнього тяжіння записується в такий спосіб:
Тут
Очевидно, що сила
Закон всесвітнього тяжіння сформульований Ньютоном, строго кажу-чи, для точкових мас. Та виявилося, що сила взаємодії між двома частин-ками не залежить від наявності третьої частинки. Це означає, що якщо взає-модіють між собою N частинок, то сила
Тут
Рис.8.1Рис.8.2
Отриманий результат називають законом адитивності. Він дає змогу засто-сувати закон всесвітнього тяжіння для знаходження сили взаємодії між двома тілами довільних розмірів і форми. Для цього необхідно умовно розбити ці тіла на велику кількість Сила
а сила
Вивчення руху тіл відносно поверхні Землі показує, що сила тяжіння Рис.8.3 альною. Отже, на таке тіло діє сумарна сила
де
Оскільки відцентрова сила залежить від географічної широти місця розта-шування тіла відносно Землі, то очевидно, що й прискорення вільного па-діння залежить від географічної широти. Розглянемо цю залежність для двох випадків: падіння тіла на полюс і на екватор Землі. Величина відцентрової сили дорівнює:
Якщо тіло падає на полюс Землі, то для нього
Тут Якщо тіло падає на екватор, то сила ваги
Тут Якщо тіло перебуває на невеликій висоті
де Із цього рівняння (а також з досвіду) випливає, що прискорення віль-ного падіння не залежить від маси, розмірів й інших властивостей тіла, а залежить від відстані
За малих висот На підставі рівняння (8.12) знаходимо, що у разі підняття тіла на висо-ту
Некулястість форми Землі ( При відносно точних розрахунках ураховується положення тіла відносно центра Землі. Поле тяжіння Закон всесвітнього тяжіння дає кількісну оцінку взаємодії, але не розкриває механізму тяжіння. Практика показує, що сила тяжіння не залежить від щільності навколишнього середовища. Таку взаємодію можна зрозуміти, якщо вважати, що всі тіла породжують навколо себе поле тяжіння (гравітаційне поле).
радіусом - вектором Розділивши сили Це рівняння виражає силу, з якою гравітаційне поле діє на тіло з одиничною масою в заданій точці простору. Цю силу називають напруженістю поля тяжіння. Позначимо її через символ
Напруженість поля є його силовою характеристикою. Якщо напруженість поля в усіх його точках однакова за величиною і за напрямком, то поле називають однорідним. Якщо в усіх точках поля його вектори напруженості спрямовані уз-довж прямих, які перетинаються в одній і тій же точці
Якщо поле утворюється кількома ( Рис.8.5
Це твердження називають принципом суперпозиції (накладання) полів, що є наслідком закону адитивності сил (рівняння (8.4)). На підставі рівнянь (8.10) і (8.9) знаходимо, що прискорення віль-ного падіння тіла дорівнює напруженості поля тяжіння в тій точці, де в розглянутий момент перебуває тіло:
Якщо тіло не вільне, то під дією поля тяжіння тіло діє на опору або підвіску із деякою силою
Сила
залежить від прискорення тіла разом з опорою або підвіскою. Силу, з якою тіло, що перебуває в полі тяжіння, діє на опору або підвіску, називають вагою тіла. При цьому передбачається, що тіло, опора і підвіска будуть у тій системі відліку, в якій визначається вага. Коли говорять про вагу тіла, то, як правило, припускають, що тіло, опора і підвіс не мають прискорення відносно Землі. Отже, вага тіла, згідно з рівнянням (8.18), дорівнює силі ваги На підставі рівняння (8.18) знаходимо: якщо опора рухається вгору із прискоренням Сили бувають консервативні, що проявляються в потенціальних по-лях, і неконсервативні, що проявляються в не потенціальних полях. З'ясуємо, до якої із цих категорій належать сили й поля тяжіння. Для цього знайдемо роботу сил поля з переміщення матеріальної точки т сила-ми тяжіння із точки 1 у точку 2 через проміжну точку
При переміщенні матеріальної точки
З рівняння (8.20) випливає, що робота Отже, сили поля тяжіння, створюваного матеріальною точкою М, є консер-вативними, а розглянуте поле – потенціальним. На основі принципу адитив-ності сил тяжіння можна показати, що отриманий висновок справедливий і для кожного поля тяжіння, створюваного будь-якою сукупністю тіл. У розділіVбуло показано, що робота
Зіставляючи рівняння (8.20) і (8.21), знаходимо:
При прагненні Оскільки точку 1 було обрано довільно, то в загальному випадку потенціальна енергія одно-го тіла в полі тяжіння, створюваного іншим ті-лом, може бути виражена рівнянням: Рис.8.6 На основі принципу суперпозиції полів можна показати, що потен-ціальна енергія матеріальної точки з масою
Потенціальну енергію матеріальної точки з одиничною масою в даній точці поля називають потенціалом поля в цій точці:
Якщо поле створюється сукупністю N матеріальних точок з масами
На підставі рівнянь (8.20), (8.21) та (8.24) знаходимо, що при робота сил поля над тілом масою
Це дає можливість надати фізичного змісту поняттям потенціальної енергії тіла в полі та потенціалу поля: потенціальна енергія тіла маси На підставі співвідношення
У загальному випадку потенціал поля може бути функцією координат і часу: Тому: де Проекції вектора
Вектор
Рівняння (8.26) виражає зв'язок між напруженістю й потенціалом поля тя-жіння в довільно обраній точці. Наведені тут положення теорії поля тяжіння можуть бути застосовані до тіл, що рухаються зі швидкостями, набагато меншими від швидкості світла в порожнечі. За великих швидкостей руху тіл треба застосовувати теорію поля тяжіння, яка базується на теорії відносності.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.011 с.) |

 , прямо пропор-ційною добутку їх мас
, прямо пропор-ційною добутку їх мас  , і
, і  і обернено пропорційною квадрату відс-тані
і обернено пропорційною квадрату відс-тані  між ними:
між ними: (8.1)
(8.1) (8.2)
(8.2) – сила, що діє на першу частинку з боку другої;
– сила, що діє на першу частинку з боку другої; 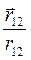 – одиничний вектор, спрямований вздовж радіуса – вектора
– одиничний вектор, спрямований вздовж радіуса – вектора  , тобто від першої частки до другої (рис.8.1) – його часто позначають символом
, тобто від першої частки до другої (рис.8.1) – його часто позначають символом  ;
; – стала тяжіння або гравітаційна стала,
– стала тяжіння або гравітаційна стала,  .
. , з якою перша частинка діє на другу, буде спрямо-вана протилежно до радіуса-вектора
, з якою перша частинка діє на другу, буде спрямо-вана протилежно до радіуса-вектора (8.3)
(8.3) , з якою діють на одну із части-нок з масою
, з якою діють на одну із части-нок з масою  всі інші частинки з масами тк, дорівнює векторній сумі сил, з якими всі N – 1 частинок діють на одну із N:
всі інші частинки з масами тк, дорівнює векторній сумі сил, з якими всі N – 1 частинок діють на одну із N: (8.4)
(8.4) – радіуси-вектори, що з'єднують частинку з масою mi з усіма іншими частинками.
– радіуси-вектори, що з'єднують частинку з масою mi з усіма іншими частинками.
 і
і  настільки малих частинок з масами
настільки малих частинок з масами  й
й  (рис. 8.2), щоб кожну з них можна було вважати матеріальною точкою. Тоді частинка
(рис. 8.2), щоб кожну з них можна було вважати матеріальною точкою. Тоді частинка  .
. з якою все друге тіло діє на одну частинку Δ mi першого тіла, відповідно до закону адитивності, буде дорівнювати:
з якою все друге тіло діє на одну частинку Δ mi першого тіла, відповідно до закону адитивності, буде дорівнювати:
 , з якою перше тіло діє на друге дорівнює:
, з якою перше тіло діє на друге дорівнює:
 (8.5)
(8.5) викликає два види руху: по-перше, тіло, позбавлене опори, падає на Землю; по-друге, воно бере участь у добовому обертанні Землі, внаслідок чого на нього діє відцентрова сила
викликає два види руху: по-перше, тіло, позбавлене опори, падає на Землю; по-друге, воно бере участь у добовому обертанні Землі, внаслідок чого на нього діє відцентрова сила  , оскільки система відліку, пов'язана із Землею, для такого тіла є неінерці-
, оскільки система відліку, пов'язана із Землею, для такого тіла є неінерці-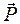 , що складається із сили тяжін-ня
, що складається із сили тяжін-ня  (8.6)
(8.6) – відстань від центра Землі до тіла. Силу
– відстань від центра Землі до тіла. Силу  . (8.7)
. (8.7) .
. :
: . (8.8)
. (8.8) – відстань від центра Землі до тіла.
– відстань від центра Землі до тіла. , що діє на це тіло, дорів-нює:
, що діє на це тіло, дорів-нює: .
.  (8.9)
(8.9) – відстань від центра Землі до тіла;
– відстань від центра Землі до тіла;  – маса Землі;
– маса Землі;  – відстань від центра Землі до полюса;
– відстань від центра Землі до полюса;  – відстань від центра до точок на екваторі.
– відстань від центра до точок на екваторі. від поверхні Землі (тобто
від поверхні Землі (тобто  ) то величина
) то величина  приблизно дорівнює 0,00345, тобто, від-центрова сила становить 0,345% від сили тяжіння. Тому в першому наближенні приймають, що сила ваги
приблизно дорівнює 0,00345, тобто, від-центрова сила становить 0,345% від сили тяжіння. Тому в першому наближенні приймають, що сила ваги  дорівнює:
дорівнює: , (8.10)
, (8.10) –прискорення тіла біля самої поверхні Землі, а
–прискорення тіла біля самої поверхні Землі, а  – прискорення тіла, що перебуває на висоті
– прискорення тіла, що перебуває на висоті  (8.11)
(8.11)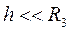 , величина
, величина  дуже мала і її можна не враховувати. Тоді
дуже мала і її можна не враховувати. Тоді 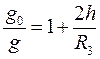 . (8.12)
. (8.12) (8.13)
(8.13)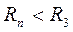 ) і вплив добового обертання (виникнення відцентрової сили) призводить до того, що прискорення сили ваги залежить від географічної широти місця й змінюється від 9,83 м/с2 на полюсах до 9,78 м/с2 на екваторі. На широті 45° воно дорівнює 9,80665м/с2. У приблизних розрахунках приймають
) і вплив добового обертання (виникнення відцентрової сили) призводить до того, що прискорення сили ваги залежить від географічної широти місця й змінюється від 9,83 м/с2 на полюсах до 9,78 м/с2 на екваторі. На широті 45° воно дорівнює 9,80665м/с2. У приблизних розрахунках приймають  =9,8 м/с2.
=9,8 м/с2. Нехай деяке тіло з масою
Нехай деяке тіло з масою  (рис. 8.4) утворює навколо себе гравітаційне поле. Розглянемо характеристики цього поля.Для цього по черзі будемо розміщувати тіла з масами
(рис. 8.4) утворює навколо себе гравітаційне поле. Розглянемо характеристики цього поля.Для цього по черзі будемо розміщувати тіла з масами 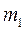 , Рис.8.4
, Рис.8.4  і
і  в точку простору, положення якої задано
в точку простору, положення якої задано


 ,
,  і
і 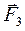 на маси
на маси 
 . Таким чином, напруженість поля тяжіння в певній точці простору виражається рівнянням:
. Таким чином, напруженість поля тяжіння в певній точці простору виражається рівнянням: (8.14)
(8.14) (рис. 8.5), нерухо-мій відносно обраної системи відліку, то поле називають центральним, а точку
(рис. 8.5), нерухо-мій відносно обраної системи відліку, то поле називають центральним, а точку  Якщо чисельне значення напруженості поля залежить тільки від відстані
Якщо чисельне значення напруженості поля залежить тільки від відстані  до центра сил
до центра сил  , то поле називають сферично симетричним. Очевидно, що поле тяжіння, створюване матеріальною точкою або однорідною кулею, є центральним і сферично симетричним.
, то поле називають сферично симетричним. Очевидно, що поле тяжіння, створюване матеріальною точкою або однорідною кулею, є центральним і сферично симетричним. ) тілами, то напруженість сумарного поля дорівнює векторній сумі напруженостей полів, утворюваних кожним з тіл:
) тілами, то напруженість сумарного поля дорівнює векторній сумі напруженостей полів, утворюваних кожним з тіл: (8.15)
(8.15) (8.16)
(8.16) . Відповідно до третього закону Ньютона опора або підвіска діють на тіло із силою
. Відповідно до третього закону Ньютона опора або підвіска діють на тіло із силою  . Обидві ці сили викликають при-скорення тіла
. Обидві ці сили викликають при-скорення тіла  , а їх геометрична сума дорівнює сумарній силі, що діє на тіло:
, а їх геометрична сума дорівнює сумарній силі, що діє на тіло: (8.17)
(8.17) (8.18)
(8.18) і залежить, строго кажучи, від положення цього тіла відносно Землі. Вагу тіла можна вважати постійною лише з тим ступенем наближення, з яким можна вважати постійним прискорення вільного падіння.
і залежить, строго кажучи, від положення цього тіла відносно Землі. Вагу тіла можна вважати постійною лише з тим ступенем наближення, з яким можна вважати постійним прискорення вільного падіння. , що еквівалентно збільшенню ваги – тіло відчуває перевантаження. Рух опори вниз із приско-ренням
, що еквівалентно збільшенню ваги – тіло відчуває перевантаження. Рух опори вниз із приско-ренням  ) настає невагомість.
) настає невагомість. (рис. 8.6). Робота
(рис. 8.6). Робота  на елементарному переміщенні
на елементарному переміщенні  дорівнює:
дорівнює:  . Оскільки:
. Оскільки:  то
то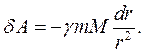 (8.19)
(8.19)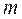 із точки 1 у точку 2 робота сил поля дорівнює:
із точки 1 у точку 2 робота сил поля дорівнює: (8.20)
(8.20) не залежить від форми траєкто-рії руху матеріальної точки т, а залежить лише від початкової й кінцевої відстаней між матеріальними точками т і М. Це означає, що
не залежить від форми траєкто-рії руху матеріальної точки т, а залежить лише від початкової й кінцевої відстаней між матеріальними точками т і М. Це означає, що  . Тоді:
. Тоді: 
 (8.21)
(8.21)

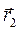 до нескінченності одержуємо:
до нескінченності одержуємо:  .
. . (8.22)
. (8.22) . (8.23)
. (8.23) . (8.24)
. (8.24) . (8.25)
. (8.25)
 , а потенціал поля
, а потенціал поля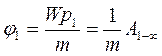 .
.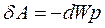 й рівняння (8.14) та (8.24) знаходимо:
й рівняння (8.14) та (8.24) знаходимо: .
. . Для стаціонарного поля, властивості якого в кожній точці простору з часом не змінюються, величина
. Для стаціонарного поля, властивості якого в кожній точці простору з часом не змінюються, величина 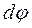 дорівнює:
дорівнює:  .
.
 – довільний напрямок.
– довільний напрямок.


 . (8.26)
. (8.26)


